Instantaneous Rate of Change
TLDRThe transcript discusses the concepts of average and instantaneous rate of change, using the function f(x) = x cubed as an example. It explains how to calculate the instantaneous rate of change by finding the derivative of the function and evaluates it at x=1, resulting in a slope of 3. The average rate of change is then explored by calculating it over different intervals and demonstrating how it converges to the instantaneous rate as the intervals become smaller. The application of these concepts is further illustrated with a second function, f(x) = x to the fourth power, and an example involving a table of distances traveled over time, where the instantaneous speed is approximated when t=15 seconds.
Takeaways
- 📈 The concept of 'average rate of change' and 'instantaneous rate of change' are introduced, highlighting their importance in understanding the behavior of functions.
- 🌟 For a given function, such as f(x) = x^3, the instantaneous rate of change at a specific point x=a is found by taking the derivative of the function and evaluating it at a.
- 🔢 The power rule is used to find the derivative of a function, exemplified by f'(x) = 3x^2 for f(x) = x^3.
- 📌 The instantaneous rate of change at x=1 for f(x) = x^3 is calculated to be 3, representing the slope of the tangent line at that point.
- 🏞️ A graph of the function f(x) = x^3 is referenced to visualize the tangent line and its slope at the point x=1.
- 🔄 The average rate of change is calculated by finding the difference in function values over a specified interval and dividing by the difference in the interval's endpoints.
- 📊 Two examples of average rate of change are provided: one between x=0 and x=2, and another between x=0.9 and x=1.1, showing how it can estimate the instantaneous rate of change when the interval is centered around the point of interest.
- 📈 The concept of 'midpoint' is emphasized as crucial for using the average rate of change to approximate the instantaneous rate of change.
- 🏢 An example with a different function, f(x) = x^4, is used to demonstrate the process of estimating the instantaneous rate of change using average rate of change with chosen x-values close to the point of interest.
- 📝 The practical application of these concepts is illustrated through a hypothetical table of values representing distance traveled over time, with the task of estimating instantaneous speed at a specific time.
- 🚀 The importance of selecting appropriate intervals for calculating average rate of change to accurately approximate instantaneous rate of change is highlighted, as seen in the distance vs. time example.
Q & A
What is the main difference between average rate of change and instantaneous rate of change?
-The average rate of change is the overall change in a function over a specified interval, calculated as the change in the function's output (y) divided by the change in its input (x). In contrast, the instantaneous rate of change is the rate at which a function changes at a specific point, which is represented by the slope of the tangent line to the function at that point.
How do you find the instantaneous rate of change for a function at a given point?
-To find the instantaneous rate of change, you first need to determine the first derivative of the function. The value of this derivative at the given point x is the instantaneous rate of change at that point.
What is the geometric interpretation of the instantaneous rate of change?
-The instantaneous rate of change corresponds to the slope of the tangent line to the curve of the function at a particular point. This slope represents how steep the function is at that point, which can be visualized as the rate at which a point on the curve is rising or falling as you move along the x-axis.
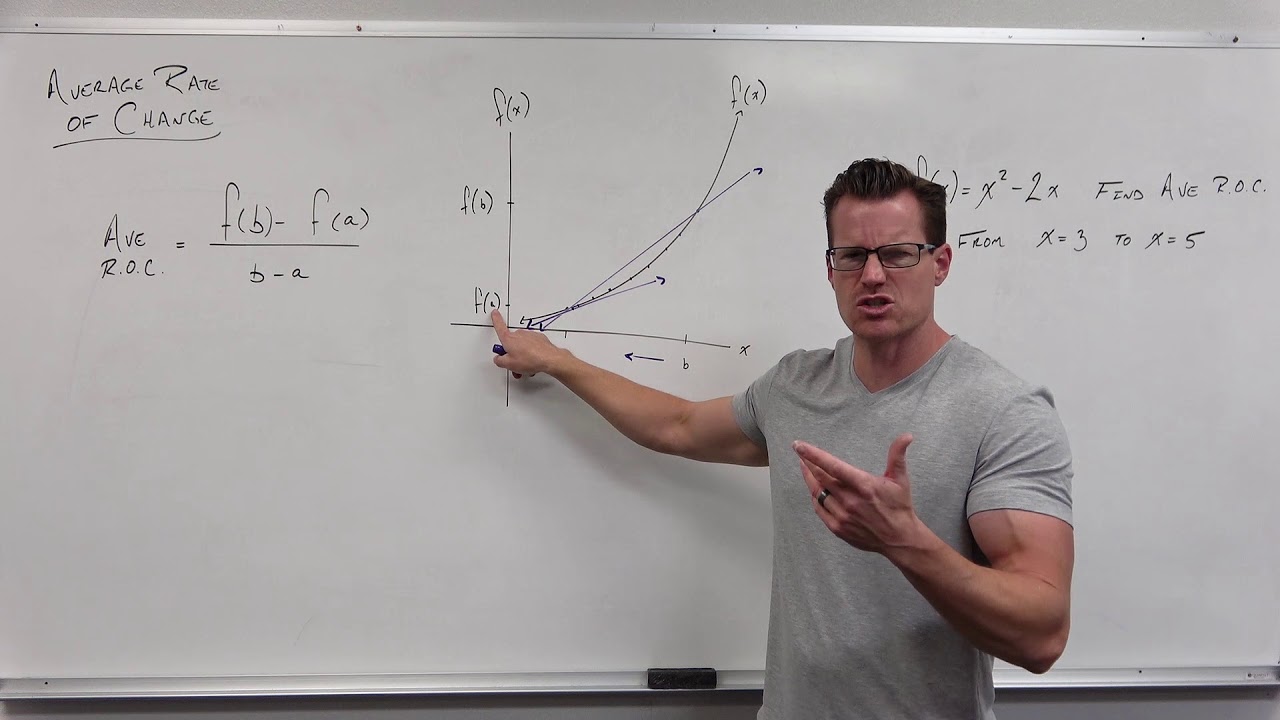
What is the formula for average rate of change and how is it calculated?
-The formula for average rate of change is given by (f(b) - f(a)) / (b - a), where 'a' and 'b' are the x-values within the interval over which the change is being calculated, and f(a) and f(b) are the corresponding y-values of the function at those points.
How can you estimate the instantaneous rate of change using average rate of change?
-You can estimate the instantaneous rate of change by choosing two x-values (a and b) that are very close to the point of interest. The closer these x-values are to each other and to the point of interest, the closer the average rate of change will be to the instantaneous rate of change at that point.
Why might you need to approximate the instantaneous rate of change?
-You might need to approximate the instantaneous rate of change if you do not have the explicit function or if you are working with a table of values rather than an analytical function. In such cases, you can use the average rate of change over an interval that contains the point of interest to estimate the instantaneous rate of change.
What is the practical application of understanding instantaneous rate of change?
-Understanding the instantaneous rate of change is important in various real-world scenarios, such as calculating the speed of a moving object at a specific time, analyzing the growth rate of a population at a particular moment, or understanding how financial markets are fluctuating at a given instant.
How does the instantaneous rate of change relate to the concept of a derivative in calculus?
-The instantaneous rate of change is the foundation of the derivative concept in calculus. The derivative of a function at a point x is defined as the limit of the average rate of change as the interval size approaches zero, which gives the instantaneous rate of change at that point.
What is the role of the power rule in finding derivatives?
-The power rule is a fundamental differentiation rule in calculus that states if f(x) = x^n, where n is a constant, then the derivative f'(x) = n * x^(n-1). This rule simplifies the process of finding derivatives for functions involving monomials.
How does the average rate of change formula relate to the concept of secant lines in geometry?
-The average rate of change formula is directly related to the concept of secant lines in geometry. A secant line is a straight line that intersects a curve at two or more points. The slope of this secant line, calculated using the average rate of change formula, represents the average change in y-values over the interval between the two points where the line intersects the curve.
What is the significance of the midpoint in estimating instantaneous rate of change?
-The midpoint is significant in estimating the instantaneous rate of change because it ensures that the interval used for the average rate of change is symmetric around the point of interest. This symmetry helps to minimize the error in the estimation, making the average rate of change a closer approximation to the instantaneous rate at that point.
Outlines
📈 Understanding Average vs. Instantaneous Rate of Change
This paragraph introduces the concepts of average and instantaneous rate of change. It uses the function f(x) = x^3 as an example to explain how to find the instantaneous rate of change at a specific point (x=1) by calculating the derivative, which in this case is f'(x) = 3x^2, resulting in an instantaneous rate of change of 3 at x=1. The paragraph further illustrates the concept of the slope of the tangent line representing this rate of change. It then contrasts this with the average rate of change, demonstrated using the same function over intervals around x=1, showing how the average rate can approximate the instantaneous rate when the interval midpoints are close to the point of interest.
🔢 Estimating Instantaneous Rate of Change Using Average Rate
This paragraph focuses on estimating the instantaneous rate of change using the average rate of change formula. It uses the function f(x) = x^4 and asks to estimate the instantaneous rate of change at x=2. The example picks two x values close to 2 (1.9 and 2.1) to calculate the average rate of change, which approximates to 3.01. The paragraph then shows how to find the exact instantaneous rate of change by deriving the function, resulting in f'(x) = 4x^3, and by plugging in x=2, the exact rate is found to be 32. The paragraph emphasizes the usefulness of the average rate of change when the function is not given or only a table of values is available.
🏃♂️ Estimating Instantaneous Speed from a Distance-Time Table
The final paragraph discusses the application of average rate of change to estimate instantaneous speed from a distance-time table. It presents a hypothetical table where the distance traveled by an object is recorded at different time intervals. The task is to estimate the instantaneous speed at t=15 seconds. The paragraph explains that the instantaneous speed can be approximated by using the average speed over the time intervals that bookend the time of interest, ensuring the chosen midpoint is as close as possible to the time being estimated. By using the distances at t=20 and t=10 (with t=15 as the midpoint), the average speed is calculated and then adjusted to estimate the instantaneous speed at t=15, resulting in an approximate speed of 2.55 meters per second.
Mindmap
Keywords
💡Average Rate of Change
💡Instantaneous Rate of Change
💡Derivative
💡Slope
💡Tangent Line
💡Power Rule
💡Midpoint
💡Estimation
💡Table of Values
💡Speed
💡Graph
Highlights
The concept of average rate of change and instantaneous rate of change is introduced.
For the function f(x) = x cubed, the instantaneous rate of change at x=1 is found by taking the derivative and evaluating at x=1.
The instantaneous rate of change at x=1 for f(x) = x cubed is 3, representing the slope of the tangent line at that point.
The average rate of change is calculated between two points by finding the difference in function values and dividing by the difference in x-values.
The average rate of change between x=0 and x=2 for f(x) = x cubed is 4, which is close to the instantaneous rate of change at x=1.
The midpoint between two intervals can be used to estimate the instantaneous rate of change using the average rate of change.
For the function f(x) = x to the fourth power, the instantaneous rate of change at x=2 is estimated using average rate of change between x=1.9 and x=2.1.
The exact instantaneous rate of change for f(x) = x to the fourth power at x=2 is found to be 32 by taking the derivative and evaluating at x=2.
Approximation of the instantaneous rate of change is useful when the function is not given, and only a table of values is available.
A table representing distance traveled over time is used to estimate the instantaneous speed of an object at t=15 seconds.
The average speed is used to approximate the instantaneous speed at t=15 by considering the distances at t=10 and t=20.
The instantaneous speed of the object at t=15 is estimated to be approximately 2.55 meters per second.
The concept of using the midpoint of two intervals to estimate the instantaneous rate of change is emphasized.
The importance of selecting intervals close to the point of interest for accurate estimation is highlighted.
The practical application of these concepts is demonstrated through the estimation of an object's instantaneous speed from a distance-time table.
The mathematical concepts discussed are applicable to various real-world scenarios, such as calculating the speed of a moving object.
The process of finding the derivative of a function (f prime of x) is explained using the power rule.
The concept of slope as the rise over run is used to explain the slope of the tangent line.
The method of estimating the instantaneous rate of change using average rate of change is detailed with examples.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: