Derivatives! The Limit Definition
TLDRThe video script introduces the concept of derivatives, which are essential for describing the rate of change of continuous functions. It begins by revisiting the difference quotient, also known as the average rate of change, and then explores the instantaneous rate of change, which is found by taking the limit as the distance between two points approaches zero. The script explains the graphical representation of this concept, illustrating how the slope of a tangent line at a point can be approximated by shrinking the distance between points. The process of finding the derivative, denoted as f'(x), is demonstrated through examples, including a simple linear function and a more complex quadratic function. The video concludes with important notes on simplifying the difference quotient before taking the limit and emphasizes that the derivative provides the instantaneous rate of change at any given point. It teases upcoming content on shortcuts to avoid calculating limits in every case.
Takeaways
- 📚 Derivatives are a fundamental topic for describing rates of change of continuous functions.
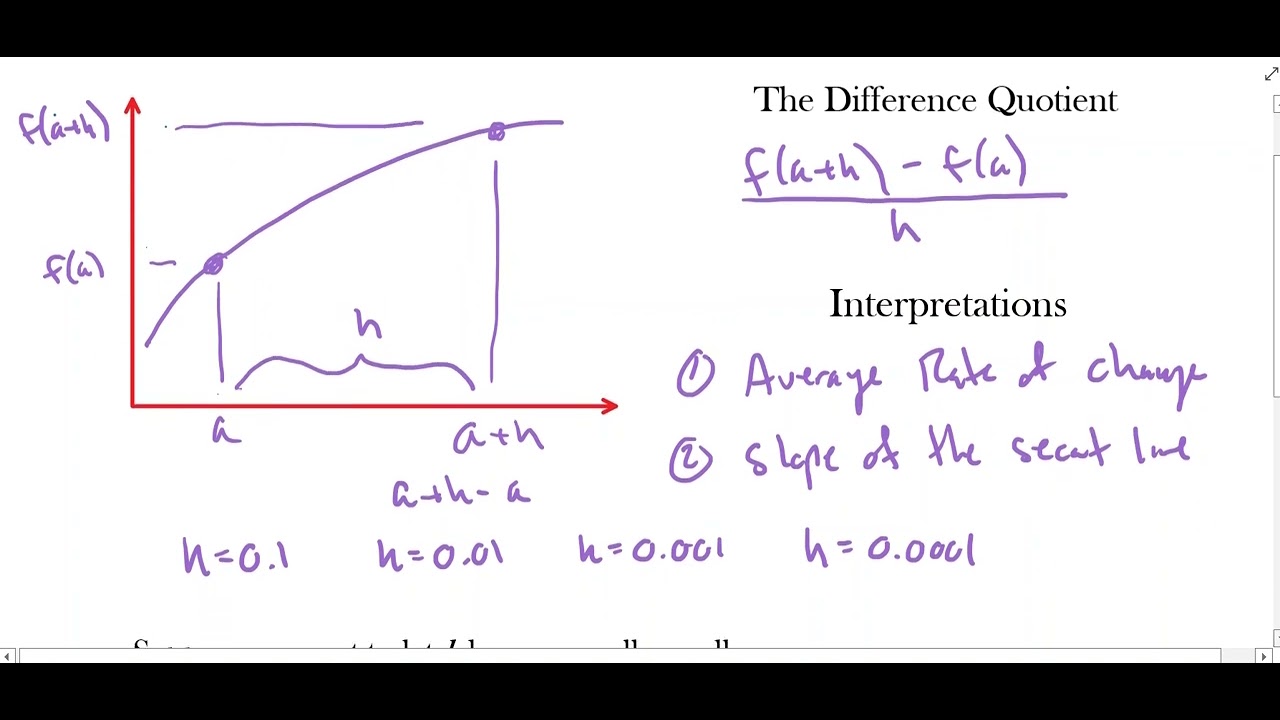
- 🔍 The difference quotient, f(X + H) - f(X) / H, represents the average rate of change between two points X and X + H.
- 🌟 As H approaches zero, the difference quotient becomes the instantaneous rate of change, which is the definition of the derivative.
- 📈 The graphical representation of the instantaneous rate of change is the slope of the tangent line to the curve at a given point.
- 🧮 The derivative, denoted as f'(X) or df/dX, is calculated by taking the limit of the difference quotient as H approaches zero.
- ✅ For the function f(X) = 2X - 4, the derivative f'(X) is a constant 2, indicating a constant rate of change.
- 🔢 For a more complex function like f(X) = 3X^2 - X + 7, the derivative f'(X) = 6X - 1 represents the instantaneous rate of change at any point X.
- 📌 Evaluating the derivative at a specific point, such as f'(1), gives the instantaneous rate of change at that point.
- 💡 Simplifying the difference quotient before taking the limit can make finding the derivative more straightforward.
- 📉 The derivative of a function is itself a function that, for any given X, provides the instantaneous rate of change of the original function at that point.
- 🚀 There are shortcuts to finding derivatives without having to calculate limits every time, which will be covered in future lessons.
Q & A
What is the main topic of the video?
-The main topic of the video is derivatives, which are used to describe rates of change of continuous functions.
What is the difference quotient and how is it used?
-The difference quotient is a formula used to find the average rate of change between two points X and X plus h, represented as (f(X + h) - f(X)) / H. It is used to find the slope of the line connecting these two points.
What is the instantaneous rate of change?
-The instantaneous rate of change is the rate of change of a function at a specific point. It is found by taking the limit of the difference quotient as the distance between the points (H) approaches zero.
How does the graphical representation of the instantaneous rate of change relate to the concept of a tangent line?
-Graphically, the instantaneous rate of change is represented by the slope of a tangent line to the curve of the function at a specific point. As the distance between the points (H) approaches zero, the secant line (green line) becomes a better approximation of the tangent line (red line).
What is the derivative of a function and how is it denoted?
-The derivative of a function is the limit of the difference quotient as H approaches zero, which gives the instantaneous rate of change at any point X. It is denoted as f'(X) or df/dX.
What is the derivative of the function f(X) = 2X - 4?
-The derivative of the function f(X) = 2X - 4 is a constant, f'(X) = 2. This indicates that the instantaneous rate of change is always 2 for any value of X.
How do you find the derivative of a more complicated function, such as f(X) = 3X^2 - X + 7?
-To find the derivative of a more complicated function, you first find the difference quotient by plugging in X + h for X in the function, then simplify the expression. After that, take the limit as H approaches zero, which often involves algebraic simplification and cancellation.
What is the derivative evaluated at X = 1 for the function f(X) = 3X^2 - X + 7?
-The derivative evaluated at X = 1 for the function f(X) = 3X^2 - X + 7 is f'(1) = 6(1) - 1 = 5. This means the instantaneous rate of change at X = 1 is 5.
What is the general process for finding the derivative of a function?
-The general process for finding the derivative involves: (1) finding the difference quotient, (2) simplifying the difference quotient, (3) taking the limit as H approaches zero, and (4) simplifying the resulting expression to find the derivative function.
Why is it important to simplify the difference quotient before taking the limit?
-Simplifying the difference quotient before taking the limit makes the process of finding the derivative more manageable and reduces the complexity of the algebraic manipulation required, making it easier to identify the terms that will cancel out.
What does the derivative of a function represent?
-The derivative of a function represents the instantaneous rate of change of the function at a given point. It is a special type of function that, for any X you plug in, gives you the instantaneous rate of change of the original function at that point.
Outlines
📈 Introduction to Derivatives and Instantaneous Rate of Change
This paragraph introduces the concept of derivatives, which are used to describe the rate of change of continuous functions. It starts by recalling the difference quotient, also known as the average rate of change, and then explores the concept of instantaneous rate of change by letting the distance between two points approach zero. The instantaneous rate of change is graphically represented as the slope of a tangent line to a curve at a given point. The process of finding this rate involves taking the limit of the difference quotient as the distance between points approaches zero, which is the definition of the derivative. The derivative is denoted as f'(x) or f(x) with a tick mark above it, and it provides both the instantaneous rate of change and the slope of the tangent line at any point x. An example is given to illustrate the process of finding the derivative of a simple function, 2x - 4, which results in a derivative of 2, indicating a constant rate of change.
🔍 Deriving the Derivative of a Quadratic Function
The second paragraph delves into finding the derivative of a more complex function, f(x) = 3x^2 - x + 7, by evaluating the derivative at x = 1. The process involves calculating the difference quotient and then simplifying it before taking the limit as h approaches zero. After algebraic manipulation, the derivative is found to be 6x - 1. Substituting x = 1 into the derivative gives an instantaneous rate of change of 5 at that point. The paragraph emphasizes the importance of simplifying the difference quotient before taking the limit and highlights that the derivative is a function that, for any given x, provides the instantaneous rate of change of the original function at that point.
📚 Summary of Derivatives and Upcoming Shortcuts
The final paragraph summarizes the process of finding derivatives using the limit definition and provides important notes for dealing with derivatives. It reiterates that the derivative of a function f(x) is given by the limit as h approaches zero of the difference quotient (f(x + h) - f(x))/h. The paragraph also hints at upcoming shortcuts that will be discussed in the next video, which will help avoid having to calculate limits every time. It encourages viewers to attempt the homework and offers well wishes for their success.
Mindmap
Keywords
💡Derivatives
💡Continuous Functions
💡Difference Quotient
💡Instantaneous Rate of Change
💡Graphical Meaning
💡Limit
💡Tangent Line
💡Derivative (F prime of X)
💡Algebra
💡Instantaneous Rate of Change at a Given Point
💡Shortcuts
Highlights
Derivatives are a key topic for understanding rates of change in continuous functions.
The difference quotient is used to calculate the average rate of change between two points X and X+h.
The instantaneous rate of change is found by taking the limit as H approaches zero in the difference quotient.
Graphically, the instantaneous rate of change corresponds to the slope of the tangent line at a point on a curve.
Derivatives can be represented as f'(X), which is shorthand for the limit of the difference quotient as H approaches zero.
The derivative of a function at a point gives the instantaneous rate of change at that point.
The derivative of the function 2x - 4 is a constant 2, indicating a constant rate of change.
For the function 3x^2 - x + 7, the derivative f'(x) is found by simplifying the difference quotient and taking the limit as H approaches zero.
The derivative f'(x) = 6x - 1 for the function 3x^2 - x + 7, which indicates the instantaneous rate of change varies with x.
Evaluating the derivative at a specific point, such as x=1, gives the instantaneous rate of change at that point.
At x=1, the instantaneous rate of change for the function 3x^2 - x + 7 is 5, indicating a slope of 5 at that point.
Derivatives are not just theoretical; they provide practical tools for analyzing the behavior of functions at specific points.
The process of finding derivatives involves algebraic manipulation and limit calculations, which can be complex but are essential for understanding rates of change.
Understanding the graphical representation of derivatives as the slope of a tangent line helps in visualizing the concept of instantaneous rate of change.
The derivative function f'(x) is a special type of function that, for any given x, provides the instantaneous rate of change of the original function f(x).
Shortcuts and techniques for finding derivatives without explicitly calculating limits will be discussed in subsequent lessons.
Practical application of derivatives includes analyzing rates of change in various real-world scenarios, such as physics and economics.
The importance of simplifying the difference quotient before taking the limit cannot be overstated for efficiency in finding derivatives.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: