Limits "at" infinity

Dr. Trefor Bazett
22 Aug 201706:36
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the behavior of certain mathematical functions as they approach infinity. It begins by examining the arctangent function, explaining its relationship with the tangent function and how it behaves as X approaches infinity, reaching a horizontal asymptote at ฯ€/2. The script then explores the tangent function's periodic nature and its asymptotes at ยฑฯ€/2. After understanding the inverse relationship between tangent and arctangent, the video moves on to the exponential function, e^X. It contrasts the behavior of e^X as X approaches negative and positive infinity, noting that e^X approaches 0 as X goes to negative infinity and diverges to infinity as X goes to positive infinity. The summary concludes by emphasizing the unique characteristics of the arctangent function and its importance in mathematical studies.

Takeaways
  • ๐Ÿ“ˆ The limit of arctangent (arctan) as X approaches infinity is ฯ€/2, which is a horizontal asymptote.
  • ๐Ÿ“‰ When X approaches negative infinity, the limit of arctan(X) is -ฯ€/2, another horizontal asymptote.
  • ๐Ÿ”„ Tangent (tan) is a periodic function with vertical asymptotes at ฯ€/2 and -ฯ€/2.
  • ๐Ÿ”„ The graph of the tangent function is flipped around the line y=x to obtain the graph of the arctangent function.
  • ๐Ÿ”„ The arctangent function is the inverse of the tangent function, similar to how e^x and ln(x) are inverses.
  • ๐Ÿšซ The domain of the tangent function, where it is defined as the inverse, is between -ฯ€/2 and ฯ€/2.
  • ๐Ÿงฎ For inverse functions, composing them in either order (f(g(x)) or g(f(x))) results in the identity function.
  • โˆž As X approaches infinity, the graph of the arctangent function 'flattens out' and approaches ฯ€/2.
  • ๐Ÿ“‰ For the exponential function e^X, as X approaches negative infinity, the function approaches a horizontal asymptote at y=0.
  • โˆž As X approaches positive infinity in the case of e^X, the function diverges to infinity and is unbounded.
  • ๐Ÿ“Š The behavior of exponential functions, such as e^X, is distinct from that of inverse trigonometric functions like arctan(X), where there's a horizontal asymptote rather than divergence.
Q & A

  • What happens to the function arctangent(X) as X approaches infinity?

    -As X approaches infinity, the function arctangent(X) approaches a value of ฯ€/2. This is because the tangent function has a vertical asymptote at ฯ€/2, and the arctangent function is the inverse of the tangent function.

  • What is the behavior of the tangent function as X approaches positive or negative infinity?

    -The tangent function oscillates between positive and negative infinity, with vertical asymptotes at ฯ€/2 and -ฯ€/2. It does not approach a single horizontal asymptote as it repeats its periodic behavior.

  • How do you determine the graph of an inverse function like arctangent(X) from the graph of the tangent function?

    -To determine the graph of the inverse function, you reflect the graph of the original function across the line y=x. This means that the x and y coordinates of the original function are swapped to create the graph of the inverse function.

  • What is a horizontal asymptote?

    -A horizontal asymptote is a horizontal line that a function approaches, but never actually reaches, as the independent variable (often denoted as x) approaches positive or negative infinity. It represents a limit that the function gets arbitrarily close to but does not exceed.

  • How does the graph of the exponential function e^x behave as X approaches positive or negative infinity?

    -As X approaches negative infinity, the graph of e^x approaches zero, effectively having a horizontal asymptote at y=0. Conversely, as X approaches positive infinity, the graph of e^x increases without bound, diverging to infinity.

  • What is the relationship between the composition of a function and its inverse?

    -When you compose a function with its inverse, the result is the identity function. This means that applying the inverse function to the result of the original function (or vice versa) returns the original input value.

  • null

    -null

  • Why is the domain of the tangent function typically restricted between -ฯ€/2 and ฯ€/2?

    -The domain of the tangent function is restricted between -ฯ€/2 and ฯ€/2 because this is the interval where the tangent function is one-to-one, which is necessary for it to have an inverse function (arctangent).

  • What is the significance of the term 'branch' when discussing the tangent function?

    -The term 'branch' refers to the different intervals of the tangent function where it is defined. The tangent function is periodic, and while it has multiple branches, the principal branch typically considered for the inverse function (arctangent) is between -ฯ€/2 and ฯ€/2.

  • How does the arctangent function behave as X approaches negative infinity?

    -As X approaches negative infinity, the arctangent function approaches a value of -ฯ€/2. This is the horizontal asymptote for the inverse function as it approaches negative infinity.

  • What is the limit of the arctangent function as X approaches a very large positive value?

    -The limit of the arctangent function as X approaches a very large positive value is ฯ€/2. This is because the arctangent function asymptotically approaches this value as X increases without bound.

  • Why is the exponential function e^x unbounded as X approaches positive infinity?

    -The exponential function e^x is unbounded as X approaches positive infinity because the function grows without limit. It continues to increase at an accelerating rate, never reaching a maximum value.

  • What is the limit of the exponential function e^x as X approaches negative infinity?

    -The limit of the exponential function e^x as X approaches negative infinity is 0. This is because the function decreases exponentially, approaching zero without ever actually reaching it.

Outlines
00:00
๐Ÿงฎ Understanding the Limit of Arctangent as X Approaches Infinity

The first paragraph delves into the concept of the limit of the arctangent function as X approaches infinity. It highlights the challenges of dealing with the tangent function's periodic behavior and its asymptotes at (ยฑฯ€/2). The author explains the relationship between the tangent and arctangent as inverse functions and uses this relationship to predict the behavior of the arctangent function. By flipping the graph of the tangent function over the line y=x, the graph of the arctangent is obtained. The paragraph emphasizes the horizontal asymptote at (ฯ€/2) for the arctangent function as X tends to infinity, indicating that the function approaches but does not exceed this value.

05:03
๐Ÿ“ˆ Limits of Exponential Functions: e^x as X Approaches Infinity and Negative Infinity

The second paragraph explores the behavior of the exponential function (e^x) as X approaches both positive and negative infinity. It contrasts the function's behavior with that of the arctangent, noting that as X approaches negative infinity, (e^x) approaches zero and has a horizontal asymptote at y=0. Conversely, as X approaches positive infinity, (e^x) grows without bound, indicating divergence to infinity. The paragraph underscores the unique characteristic of exponential functions to have one horizontal asymptote and to diverge to infinity on the other side, showcasing the fundamental differences in the limit behavior of various mathematical functions.

Mindmap
Keywords
๐Ÿ’กLimit
A limit in calculus is the value that a function or sequence 'approaches' as the input (or index) approaches some value. In the video, the concept of limits is central to understanding the behavior of functions as they approach infinity. For instance, the script discusses the limit of the arctangent function as X approaches infinity, which is a key concept in the video's exploration of mathematical functions and their asymptotic behavior.
๐Ÿ’กAsymptote
An asymptote is a line that a function approaches but never actually reaches. In the context of the video, the script describes horizontal asymptotes, which are horizontal lines that a function like arctangent approaches as the input (X) goes to positive or negative infinity. The video explains that arctangent has a horizontal asymptote at ฯ€/2 and -ฯ€/2, which are the limits as X goes to positive and negative infinity, respectively.
๐Ÿ’กArctangent
Arctangent, often abbreviated as arctan or tan^(-1), is the inverse trigonometric function of the tangent function. It is used to find the angle whose tangent is a given number. In the video, the script explores the limit of the arctangent function as X approaches infinity, which is a fundamental concept in understanding the behavior of inverse trigonometric functions.
๐Ÿ’กTangent
The tangent function, represented as tan or tan(x), is a trigonometric function that describes the ratio of the length of the opposite side to the length of the adjacent side in a right-angled triangle. The video discusses the periodic behavior of the tangent function and how it relates to the arctangent function through the concept of inverse functions.
๐Ÿ’กPeriodic Function
A periodic function is a type of function that repeats its values at regular intervals or periods. In the video, the tangent function is described as periodic, with its graph showing repeated patterns. This periodicity is important in understanding the behavior of the tangent function and, by extension, its inverse, the arctangent.
๐Ÿ’กInverse Function
An inverse function is a function that 'reverses' another function, so that applying the original function and then its inverse (or vice versa) returns the original input. The script explains that tangent and arctangent are inverse functions, which is why their graphs are reflections of each other across the line y=x.
๐Ÿ’กGraph
In mathematics, a graph is a visual representation of a function's relationship between two variables. The video script uses the graph of the tangent function to illustrate its periodic nature and to derive the graph of its inverse, the arctangent function, by reflecting it across the line y=x.
๐Ÿ’กExponential Function
An exponential function is a function of the form f(x) = a^x, where a is a positive real number not equal to 1. The video discusses the behavior of the exponential function e^x as X approaches positive and negative infinity, noting that it diverges to infinity for positive infinity and approaches zero for negative infinity.
๐Ÿ’กDivergence
Divergence in calculus refers to a situation where a function's values get arbitrarily large (or small, in the case of negative divergence) as the input approaches a certain value. In the video, the script describes the exponential function e^x as diverging to infinity as X approaches positive infinity, which is a key characteristic of exponential growth.
๐Ÿ’กHorizontal Asymptote
A horizontal asymptote is a horizontal line that a function approaches, but never actually reaches, as the input variable increases or decreases without bound. The video script discusses the concept of horizontal asymptotes in relation to both the arctangent and exponential functions, noting their positions and implications for the functions' behavior.
๐Ÿ’กNatural Logarithm
The natural logarithm, often denoted as ln(x), is the logarithm of a number to the base e (Euler's number, approximately equal to 2.71828). Although not explicitly detailed in the script, the concept is implied when discussing inverse functions, as the natural logarithm is the inverse of the exponential function e^x.
Highlights

The limit of arctangent of X as X goes to infinity is approached by considering the behavior of the tangent function and its inverse, the arctangent.

The tangent function has a periodic nature with asymptotes at plus or minus PI over 2.

The graph of the tangent function exhibits vertical asymptotes at these points.

Arctangent is the inverse function of tangent, and its graph is obtained by reflecting the tangent graph across the line y=x.

The domain for which the tangent function is defined as an inverse is between minus PI over 2 and PI over 2.

As X grows larger, the graph of arctangent approaches a horizontal asymptote at PI over 2.

The limit of arctangent of X as X goes to negative infinity approaches a horizontal asymptote at minus PI over 2.

The arctangent function is particularly useful and will be frequently used in mathematical courses.

The natural exponential function e^x has a horizontal asymptote at y=0 as X goes to negative infinity.

As X approaches positive infinity, e^x grows without bound, demonstrating unbounded behavior.

The behavior of exponential functions is such that there is one horizontal asymptote and divergence to infinity as X increases.

The concept of horizontal asymptotes is crucial in understanding the long-term behavior of functions as they approach infinity.

The arctangent function's graph flattens out as X approaches infinity, unlike the oscillating behavior of the tangent function.

The inverse function property is that composing the function with its inverse results in the identity function.

The notation arctan(x) with an exponent of -1 refers to the inverse function, not the reciprocal of the tangent function.

The arctangent function has a single major branch between -PI/2 and PI/2, which is the interval for which it is defined as an inverse of the tangent function.

The limit of the tangent function as X approaches positive infinity is PI/2, which is a horizontal asymptote of the arctangent function.

The limit of the exponential function e^x as X approaches negative infinity is 0, indicating a horizontal asymptote at y=0.

Transcripts

Browse More Related Video

Infinite Limit vs Limits at Infinity of a Composite Function

Limits at Infinity & Horizontal Asymptotes

Math 133 Lecture 2 6

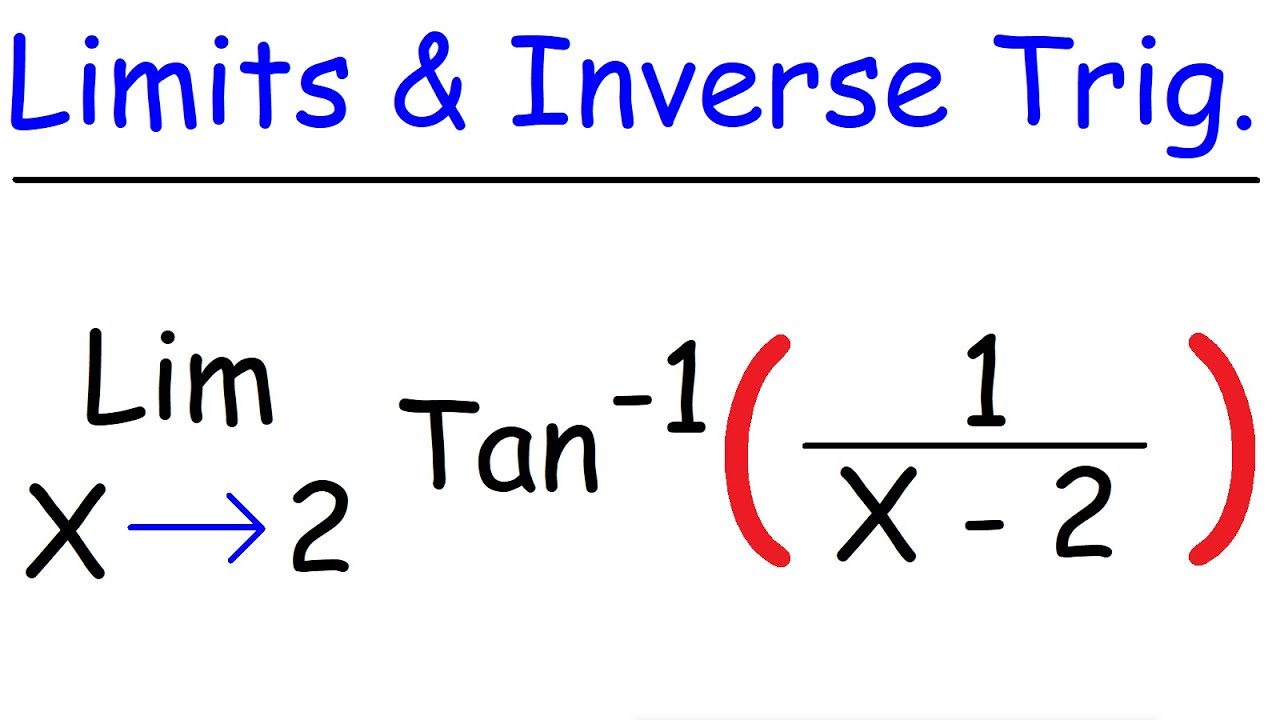
Limits of Inverse Trigonometric Functions | Calculus

Graphing the Arctan Function | MIT 18.01SC Single Variable Calculus, Fall 2010

Finding limits at infinity using squeeze theorem | Squeeze or Sandwich Theorem - Calculus

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsLimitsAsymptotesArctangentExponentialTrigonometricInverse FunctionsGraph AnalysisDivergenceEducational Content