Introduction to infinite limits | Limits and continuity | AP Calculus AB | Khan Academy

Khan Academy
21 Aug 201804:23
EducationalLearning
32 Likes 10 Comments

TLDRThis video script delves into the concept of limits in calculus, specifically focusing on the behavior of functions as the variable X approaches zero and one. It clarifies the difference between unbounded functions and those approaching infinity, introducing the notation for positive and negative infinity. The script uses examples from Khan Academy to illustrate how to determine if a limit equals infinity based on the direction from which X approaches a value, emphasizing the importance of one-sided limits in such scenarios.

Takeaways
  • ๐Ÿ“ˆ The script discusses the graphs of Y = 1/X^2 and Y = 1/X, focusing on the behavior as X approaches zero.
  • ๐Ÿšซ As X approaches zero from the left in 1/X^2, the value is unbounded in the positive direction.
  • ๐Ÿšซ Similarly, as X approaches zero from the right in 1/X^2, the value is unbounded in the positive direction.
  • ๐Ÿ“Š The concept of limits being unbounded is introduced, with the notation of approaching infinity (โˆž) being explained.
  • ๐Ÿ”„ For 1/X, the limit from the left is negative infinity (-โˆž), and from the right is positive infinity (โˆž).
  • ๐ŸŒ One-sided limits can be considered for functions approaching a point from different directions.
  • ๐Ÿ“š The script references Khan Academy for further study on one-sided limits.
  • ๐Ÿ“ An example problem is presented, involving identifying graphs that have a limit of H(X) approaching infinity as X approaches 1.
  • ๐Ÿšซ Graph A is ruled out because the limits from the left and right do not agree on the direction of infinity.
  • โœ… Graph B is a potential match because the limits from both directions approach the same infinity (positive infinity).
  • ๐Ÿšซ Graph C is also ruled out as the limits from the left and right approach different infinities (negative and positive).
Q & A

  • What were the two functions explored in the previous video?

    -The two functions explored in the previous video were Y equals one over X squared and Y equals one over X.

  • What happens to the value of one over X squared as X approaches zero from the left?

    -As X approaches zero from the left, the value of one over X squared becomes unbounded in the positive direction.

  • How is the limit of one over X squared as X approaches zero from the right described?

    -The limit of one over X squared as X approaches zero from the right is also described as unbounded in the positive direction.

  • What new notation is introduced in this video to describe the behavior of certain limits?

    -The new notation introduced in this video is the use of infinity to describe the behavior of certain limits that are unbounded.

  • What is the difference between the limit of one over X as X approaches zero from the left and from the right?

    -The limit of one over X as X approaches zero from the left is equal to negative infinity, while from the right, it is equal to positive infinity.

  • What is a one-sided limit and how does it apply to the function one over X near zero?

    -A one-sided limit is a limit that is considered from only one direction, either from the left or the right. For the function one over X near zero, one can consider the left-sided limit as approaching negative infinity and the right-sided limit as approaching positive infinity.

  • What does the statement 'the limit does not exist' mean in the context of the video?

    -In the context of the video, 'the limit does not exist' means that the function does not approach a specific finite value as X approaches a certain point, such as zero in the case of one over X.

  • What is the significance of asymptotes in the provided example problem?

    -Asymptotes are lines that a function approaches but never actually intersects. In the provided example problem, the dashed lines represent asymptotes, which help in determining the behavior of the function near the value of X where the limit is being considered.

  • Which graph in the example problem meets the condition that the limit as X approaches 1 of H of X is equal to infinity?

    -Graph B meets the condition that the limit as X approaches 1 of H of X is equal to infinity, as it approaches the same direction of infinity (positive infinity) from both the left and the right.

  • How can one determine if a limit is unbounded in the negative direction?

    -A limit is determined to be unbounded in the negative direction when, as X approaches a certain value, the function value decreases without bound, meaning it goes towards negative infinity.

  • What is the role of Khan Academy in the context of this video?

    -Khan Academy is mentioned as a resource for further learning and review, particularly for concepts such as one-sided limits which are not fully explained in the video but are relevant to understanding the behavior of certain functions near specific points.

Outlines
00:00
๐Ÿ“š Understanding Limits and Infinity in Graphs

This paragraph discusses the concept of limits in mathematical functions, particularly focusing on the behavior of 1/X and 1/X^2 as X approaches zero. The instructor explains the difference between the left-hand and right-hand limits and introduces the notation for infinity. It also touches on the concept of one-sided limits and provides an example problem from Khan Academy to illustrate these ideas.

Mindmap
Keywords
๐Ÿ’กGraphs
Graphs are visual representations of data or functions, used to display relationships and trends between variables. In the context of the video, graphs are used to illustrate the behavior of mathematical functions, specifically Y = 1/X^2 and Y = 1/X, as X approaches zero. The visual aspect of graphs helps in understanding the limits and the direction of unboundedness of the functions.
๐Ÿ’กLimits
In mathematics, a limit is a fundamental concept describing the behavior of a function as the input (or argument) approaches a particular value. The video discusses the limits of the functions as X approaches zero, exploring whether the function values approach infinity, negative infinity, or do not exist.
๐Ÿ’กInfinity
Infinity is a concept representing an unbounded quantity, larger than any real number. In the video, the term is used to describe the limit of certain functions as they increase without bound. Positive infinity indicates that the function values are increasing withoutไธŠ้™, while negative infinity indicates that they are decreasing withoutไธ‹้™.
๐Ÿ’กAsymptotes
An asymptote is a line that a curve approaches but never intersects, used to describe the end behavior of a function. In the video, dashed lines represent asymptotes, helping viewers understand the direction in which the graph of a function approaches but never reaches a certain value, such as infinity.
๐Ÿ’กUnbounded
Unbounded refers to a function that does not have a limit as the input approaches a certain value. It means that the function can increase or decrease indefinitely without any constraints. In the video, the term is used to describe the behavior of 1/X and 1/X^2 functions as X approaches zero, where the function values can increase without limit in certain directions.
๐Ÿ’กOne over X squared
The function 'one over X squared' (1/X^2) is a mathematical function where the value of Y is the reciprocal of the square of X. This function is significant in calculus, particularly when dealing with limits, as it exhibits unbounded behavior as X approaches zero from both the positive and negative sides.
๐Ÿ’กOne over X
The function 'one over X' (1/X) is a mathematical function that represents the reciprocal of X. This function is important in understanding limits and the behavior of functions as they approach certain values, especially zero. The video script discusses the limit of this function as X approaches zero, highlighting the concept of one-sided limits and the behavior of the function from both the left and the right of zero.
๐Ÿ’กOne-sided limits
One-sided limits refer to the behavior of a function as it approaches a certain point from one direction only. Unlike two-sided or 'all-sided' limits, which consider the function's behavior from both sides of the point, one-sided limits focus on either the left or the right approach. The video script uses the concept of one-sided limits to explain the behavior of the function 1/X as X approaches zero from the left and from the right.
๐Ÿ’กKhan Academy
Khan Academy is a non-profit educational organization that provides free online courses, lessons, and practice exercises in various subjects, including mathematics. In the video, the instructor encourages viewers to review the concept of one-sided limits on Khan Academy if they are not familiar with it.
๐Ÿ’กNegative infinity
Negative infinity is a concept used to describe an infinitely small value or a value that is smaller than any negative number. In the context of the video, it is used to describe the limit of the function 1/X as X approaches zero from the left, indicating that the function values decrease without bound.
๐Ÿ’กPositive infinity
Positive infinity is a concept representing an infinitely large value or a value that is larger than any positive number. In the video, it is used to describe the limit of certain functions as they increase without an upper bound. The script introduces the notation of limits going to positive infinity for the function 1/X^2 as X approaches zero from the right.
Highlights

In a previous video, the graphs of Y equals one over X squared and one over X were explored.

The limit of one over X squared as X approaches zero from the left was found to be unbounded in the positive direction.

The limit of one over X squared as X approaches zero from the right was also unbounded in the positive direction.

New notation is introduced to describe the limit as X approaches a value, such as positive or negative infinity.

The limit of one over X as X approaches zero from the left is negative infinity.

The limit of one over X as X approaches zero from the right is positive infinity.

One-sided limits can be considered when approaching a point from different directions result in different behaviors.

Khan Academy is recommended for further study on one-sided limits.

Example problem from Khan Academy involves determining which graph's limit approaches infinity as X approaches 1.

Graph A's limit as X approaches 1 from both directions does not equal infinity due to differing behaviors.

Graph B's limit as X approaches 1 from both directions appears to equal positive infinity, meeting the example's criteria.

Graph C's limit as X approaches 1 from both directions does not equal the same infinity, failing to meet the example's criteria.

The concept of limits and infinity is crucial in understanding the behavior of functions at particular points.

Asymptotes, represented by dashed lines in graphs, can provide insights into the behavior of functions as they approach certain values.

The mathematical notation for describing limits and infinity helps in communicating the behavior of functions more precisely.

The video content is educational and serves to clarify the understanding of mathematical concepts related to limits.

Transcripts

Browse More Related Video

Limits via Graphs!

Business Calculus - Math 1329 - Section 1.5 (and 1.6) - Limits and Continuity

Limit examples (part 2) | Limits | Differential Calculus | Khan Academy

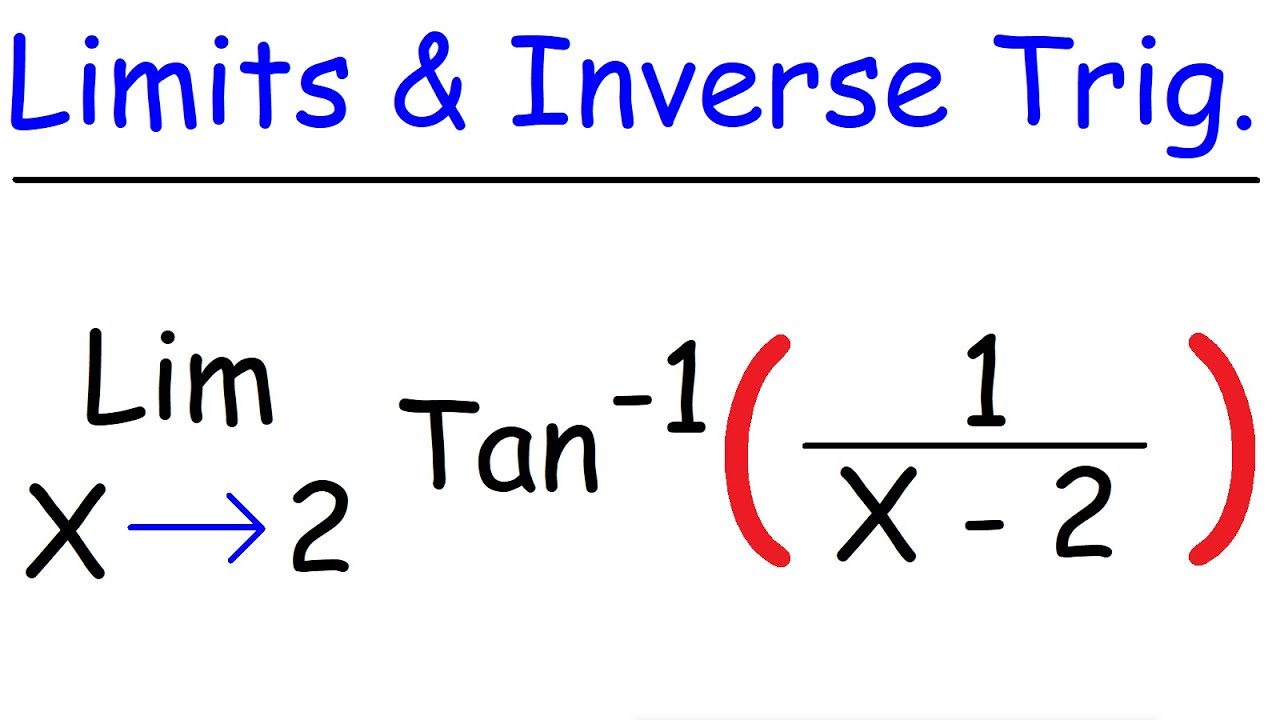
Limits of Inverse Trigonometric Functions | Calculus

Limits at infinity of quotients (Part 2) | Limits and continuity | AP Calculus AB | Khan Academy

One-sided limits from tables | Limits and continuity | AP Calculus AB | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusLimitsInfinityOneOverXOneOverXSquaredAsymptotesKhanAcademyEducationMathematicsGraphAnalysis