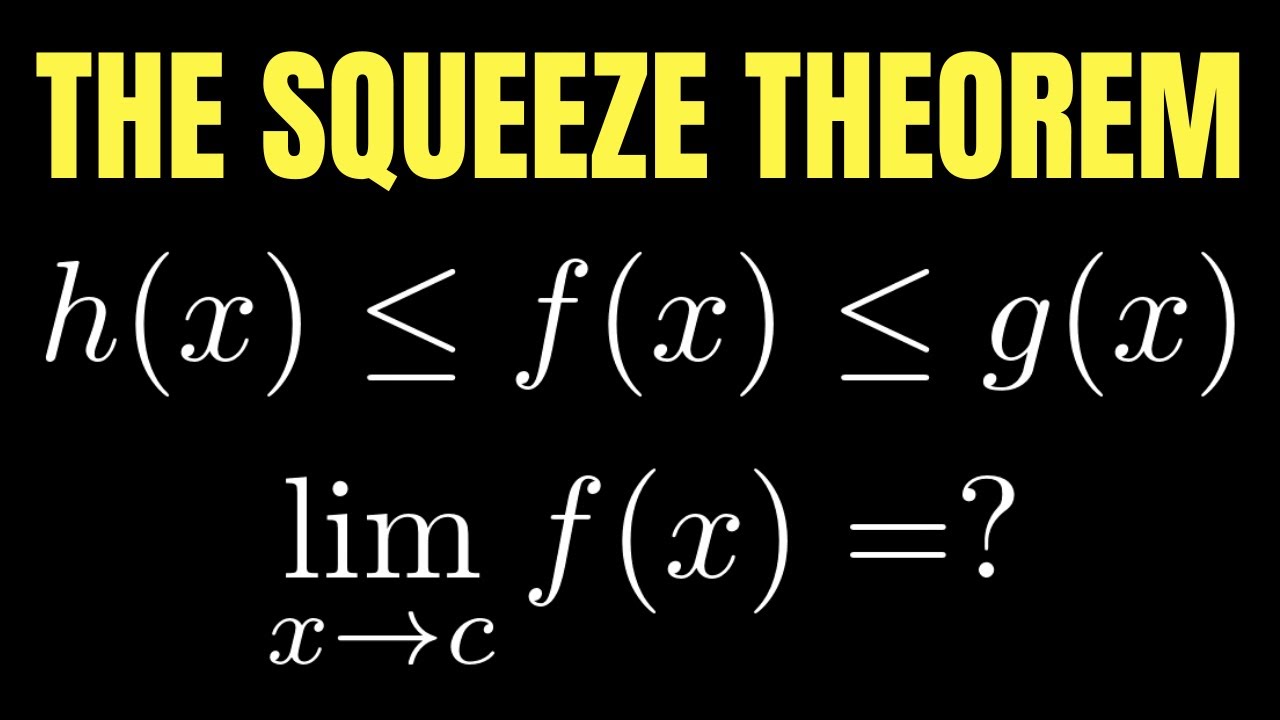Finding limits at infinity using squeeze theorem | Squeeze or Sandwich Theorem - Calculus
TLDRThis video script explores the application of the Squeeze (Sandwich) Theorem in finding limits of trigonometric functions as they approach infinity. The presenter begins by illustrating the process of finding the limit of sine x over x as x approaches infinity, noting that direct substitution is not possible due to the oscillatory nature of the sine function. Instead, the Squeeze Theorem is applied, leveraging the fact that sine values oscillate between -1 and 1. The script then moves on to demonstrate the theorem with two additional examples: the limit of cosine to the power of 2x over x squared plus 9 as x approaches infinity, and the limit of e to the power of negative x times cosine of 2x as x approaches infinity. In each case, the presenter shows how to manipulate the expressions to apply the Squeeze Theorem, ultimately concluding that the limits of the given functions are zero. The explanation is clear, emphasizing the importance of understanding the behavior of exponential and trigonometric functions when dealing with limits at infinity.
Takeaways
- 📚 The Squeeze Theorem (also known as the Sandwich Theorem) is a method used to find limits when direct substitution is not possible, particularly with trigonometric functions.
- 🚫 Direct substitution cannot be used to find the limit of \( \sin(x)/x \) as \( x \) approaches infinity because \( \sin(\infty) \) does not exist.
- 🔢 Trigonometric functions like sine and cosine oscillate between -1 and 1, which can be used to create inequalities that help apply the Squeeze Theorem.
- 📉 When applying the Squeeze Theorem, if both the left and right functions have the same limit as \( x \) approaches a certain value, the middle function's limit will also be the same.
- 🧮 To use the Squeeze Theorem, inequalities are manipulated so that the function of interest is 'sandwiched' between two other functions whose limits are known.
- ➗ In the example of \( \sin(x)/x \), dividing the inequality by \( x \) helps to transform it into the desired form for the Squeeze Theorem.
- 🔄 The limit of \( 1/x \) and \( -1/x \) as \( x \) approaches infinity is zero, which is a key step in determining the limit of \( \sin(x)/x \) using the Squeeze Theorem.
- 📌 For \( \cos^2(x)/(x^2 + 9) \), it's noted that \( \cos^2(x) \) is always between 0 and 1, which is important for setting up the Squeeze Theorem.
- 📘 When \( x \) approaches infinity, the limit of any number divided by \( x^2 + 9 \) (or any higher power of \( x \)) is zero, as the denominator grows without bound.
- 🌌 The graph of \( y = e^x \) is crucial for understanding the limits of exponential functions as the exponent approaches positive or negative infinity.
- 🧨 It's incorrect to write \( e^{-\infty} = 0 \) or \( e^{+\infty} = \infty \) in a strict mathematical sense, but these expressions are useful for conceptual understanding.
- 📨 The process of finding limits using the Squeeze Theorem involves finding the limits of the simpler functions that 'squeeze' the function of interest from both sides.
Q & A
What is the Squeeze Theorem, also known as the Sandwich Theorem, used for?
-The Squeeze Theorem is used for finding limits that cannot be determined by direct substitution, particularly when the function involves trigonometric functions or other expressions that oscillate or tend towards certain values as the variable approaches a limit.
Why can't we find the limit of sine(x)/x as x approaches infinity by direct substitution?
-Direct substitution is not possible because sine(x) does not approach a specific value as x approaches infinity; instead, it oscillates between -1 and 1. Hence, we use the Squeeze Theorem to find the limit.
What are the general bounds for the sine function?
-The sine function oscillates between -1 and 1, meaning that for any angle, the value of sine is always between these two limits.
How do we apply the Squeeze Theorem to find the limit of sine(x)/x as x approaches infinity?
-We apply the Squeeze Theorem by recognizing that sine(x) is always between -1 and 1. By dividing these inequalities by x, we create new inequalities with sine(x)/x in the middle. As x approaches infinity, both the left and right functions approach zero, and thus, by the Squeeze Theorem, the middle function also approaches zero.
What is the limit of cosine^2(x)/(x^2 + 9) as x approaches infinity?
-The limit of cosine^2(x)/(x^2 + 9) as x approaches infinity is 0. This is because cosine^2(x) is always between 0 and 1, and as x approaches infinity, the denominator (x^2 + 9) grows without bound, making the entire fraction approach zero.
Why do we say cosine^2(x) is between 0 and 1 instead of -1 and 1?
-We say cosine^2(x) is between 0 and 1 because cosine squared is always non-negative, and since it's a squared value, it cannot be less than zero. It is more accurate to reflect the nature of the function, which is always positive.
How do we find the limit of e^(-x)cosine(2x) as x approaches infinity?
-We use the Squeeze Theorem by multiplying the inequalities of -1 ≤ cosine(2x) ≤ 1 by e^(-x). As x approaches infinity, e^(-x) approaches zero, regardless of the value of cosine(2x). Therefore, the limit of the left and right functions is zero, and so is the limit of the middle function.
What happens to an exponential function with base greater than 1 when the exponent approaches negative infinity?
-When the exponent approaches negative infinity in an exponential function with a base greater than 1, the value of the function approaches zero.
Is it correct to write e^(-infinity) equals zero?
-It is not mathematically correct to write e^(-infinity) = 0 because infinity and negative infinity are not numbers. However, it is a common way to conceptualize that the exponential function approaches zero in such cases.
What is the limit of e^(-x) when x approaches infinity?
-The limit of e^(-x) as x approaches infinity is zero. This is because as x becomes larger, the exponent becomes more negative, causing the exponential function to approach zero.
What is the key takeaway from the examples provided in the video script?
-The key takeaway is the application of the Squeeze Theorem to find limits involving trigonometric functions or expressions that cannot be determined by direct substitution, especially when the variable approaches infinity.
How does the Squeeze Theorem help in understanding the behavior of functions as they approach certain limits?
-The Squeeze Theorem helps by providing a method to determine the limit of a function by 'sandwiching' it between two other functions whose limits are known. If the limits of the outer functions are the same, the limit of the middle function must also be the same, giving insight into its behavior as it approaches a particular limit.
Outlines
📚 Introduction to Squeeze Theorem for Limits
This paragraph introduces the concept of the squeeze theorem, which is used to find limits of functions that are challenging to evaluate directly. The example of the limit of sine x over x as x approaches infinity is used to illustrate the process. The presenter explains that direct substitution is not possible due to the oscillating nature of the sine function between -1 and 1. Instead, the squeeze theorem is applied by acknowledging the bounds of the sine function and then dividing all parts of the inequality by x. The limits of both the left and right sides of the inequality approach zero as x approaches infinity, thus concluding that the limit of sine x over x is also zero.
🧮 Squeeze Theorem Applied to Cosine Function
The second paragraph delves into applying the squeeze theorem to a different function, specifically cosine to the power of 2x over x squared plus 9 as x approaches infinity. The presenter clarifies that cosine squared is always positive and lies between 0 and 1. By dividing the entire inequality by x squared plus 9, the left and right expressions simplify to 0/(x^2 + 9) and 1/(x^2 + 9), respectively, both of which have a limit of zero as x approaches infinity. Consequently, the limit of the middle function, cosine squared x over x squared plus 9, is also zero, fulfilling the conditions of the squeeze theorem.
🚀 Squeeze Theorem for Exponential and Cosine Functions
The third paragraph presents a more complex example involving the limit of e to the power of negative x times cosine of 2x as x approaches infinity. The direct substitution method is inapplicable due to the cosine function's argument becoming infinite. The squeeze theorem is again used, with the cosine function bounded between -1 and 1. By multiplying all parts of the inequality by e to the power of negative x, the left and right expressions become negative e to the power of negative x and e to the power of negative x, respectively. As x approaches infinity, both the left and right expressions tend to zero because the exponential function with a negative exponent approaches zero. Therefore, the limit of the middle function, e to the negative x times cosine of 2x, is also zero.
📢 Conclusion and Viewer Engagement
The final paragraph serves as a conclusion to the video, encouraging viewers to subscribe to the channel if they enjoyed the content. It summarizes the successful application of the squeeze theorem in finding limits of various trigonometric functions as their arguments approach infinity. The presenter also hints at additional examples and further explanations in upcoming videos, inviting viewers to continue learning with the channel.
Mindmap
Keywords
💡Squeeze Theorem
💡Limit
💡Trigonometric Functions
💡Direct Substitution
💡Oscillation
💡Exponential Function
💡Infinity
💡Periodic Function
💡Cosine Function
💡Graph
💡Negative Infinity
Highlights
Introduction to using the squeeze theorem to find limits of trigonometric functions as x approaches infinity.
Direct substitution cannot be used for sine x over x as x approaches infinity due to the oscillating nature of sine.
Sine and cosine functions oscillate between -1 and 1, which is key to applying the squeeze theorem.
Division by x is used to transform the inequality to match the expression sine x over x.
The limit of 1/x and -1/x as x approaches infinity is zero, which helps in applying the squeeze theorem.
The squeeze theorem is applied to conclude that the limit of sine x over x as x approaches infinity is zero.
The process of finding limits using the squeeze theorem involves finding the limits of simpler functions on either side of the expression of interest.
Limit of cosine^2x over x^2 + 9 as x approaches infinity is proven to be 0 using the squeeze theorem.
Any expression to the power of 2 is always greater than zero, which is important for the inequality setup.
Division by (x^2 + 9) is used to align the inequality with the expression cosine^2x over x^2 + 9.
The limits of 0 over (x^2 + 9) and 1 over (x^2 + 9) as x approaches infinity are both zero.
The limit of e^(-x) * cosine(2x) as x approaches infinity is found using the squeeze theorem.
Multiplication by e^(-x) is used to transform the inequality for the expression e^(-x) * cosine(2x).
The limit of e^(-x) as x approaches infinity is zero, which is derived from the properties of exponential functions.
The graph of y = e^x is used to visualize the behavior of exponential functions as the exponent approaches infinity or negative infinity.
The limit of negative e^(-x) as x approaches infinity is also zero, which completes the application of the squeeze theorem.
The conclusion that the limit of e^(-x) * cosine(2x) as x approaches infinity is zero is reached.
The video concludes with a summary of the process and the results of applying the squeeze theorem to various limits.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: