Limits at Infinity & Horizontal Asymptotes
TLDRThis transcript delves into the concept of limits at infinity in calculus, illustrating how to determine the behavior of functions as their input approaches infinitely large or negative values. It explains the limits of 1/x as x approaches positive and negative infinity, emphasizing the results are zero from both directions. The video further explores limits of more complex functions, including rational functions and those involving exponents and roots, using step-by-step examples to demonstrate the process. It also touches on the behavior of the arctangent function and the exponential function e to the power of negative x, reinforcing the understanding of asymptotic behavior in calculus.
Takeaways
- 📈 The limit of 1/x as x approaches infinity is zero, representing a vertical asymptote at x=0 on the graph of 1/x.
- 📉 Similarly, the limit of 1/x as x approaches negative infinity is also zero, but from the left side of the vertical asymptote.
- 🌐 The graph of 1/x has both a vertical asymptote at x=0 and a horizontal asymptote at y=0, indicating the function approaches but never reaches zero as x increases without bound.
- 🔢 For any function of the form 1/x^r, where r is a positive integer, the limit as x approaches infinity is always zero due to the denominator's growing without bound.
- 📚 When dealing with rational functions where the degree of the numerator is less than the degree of the denominator, the limit as x approaches infinity is zero.
- 🔄 For rational functions with equal degrees in the numerator and denominator, the limit can be found by dividing the leading coefficients (e.g., the limit of (8x - 5)/ (2x + 3) as x approaches infinity is 4).
- 🚀 When the highest power in both the numerator and denominator is the same, terms with lower powers become insignificant, and the limit can be approximated by comparing the coefficients of the highest powers.
- 🥂 For functions involving square roots and higher powers, the limit as x approaches infinity can often be simplified by focusing on the most significant terms and applying the limit rules.
- 📈 The arctangent function approaches pi/2 (90 degrees) as x approaches infinity and approaches -pi/2 (-90 degrees) as x approaches negative infinity.
- 🌌 The limit of e^(-x) as x approaches infinity is zero, reflecting the behavior of the exponential function as it approaches zero in the limit.
Q & A
What is the limit of 1/x as x approaches infinity?
-The limit of 1/x as x approaches infinity is 0. As the denominator becomes very large, the value of the fraction approaches zero.
What is the limit of 1/x as x approaches negative infinity?
-The limit of 1/x as x approaches negative infinity is also 0. However, it approaches zero from the left side, indicating that the function approaches negative infinity and then levels off to zero as x continues to decrease.
How does the graph of 1/x behave as x approaches infinity?
-The graph of 1/x has a vertical asymptote at x=0 and a horizontal asymptote at y=0. As x increases without bound, the graph approaches the horizontal asymptote, indicating that y (the function's output) approaches zero.
What is the limit of 1/x^2 as x approaches infinity?
-The limit of 1/x^2 as x approaches infinity is 0. This is because as x becomes very large, the value of 1 divided by an even larger number (x squared) becomes an increasingly small value, tending towards zero.
What is the general theorem for the limit of 1/x^r as x approaches infinity?
-The general theorem states that the limit of 1/x^r as x approaches infinity is 0 for any positive value of r. This is because the denominator's value grows without bound, making the fraction approach zero.
How does the limit calculation change for a rational function with the same degree in the numerator and denominator?
-For a rational function where the degree of the numerator is the same as the denominator, you can divide the coefficients of the highest degree terms to find the limit. This simplifies the function to a constant ratio as x approaches infinity.
What is the limit of (8x - 5) / (2x + 3) as x approaches infinity?
-The limit of (8x - 5) / (2x + 3) as x approaches infinity is 4. This is found by dividing the coefficients of the x terms, which are the terms with the highest degree in the numerator and denominator.
How does the limit of a function involving x cubed approach as x becomes very large?
-The limit of a function involving x cubed as x approaches infinity will be dominated by the term with x cubed. All other terms become insignificant compared to the cubic term, and the limit can be found by simplifying the expression to just the cubic term and its coefficient.
What is the limit of the square root of (16x^2 - 8) / (2x - 5) as x approaches infinity?
-The limit of the square root of (16x^2 - 8) / (2x - 5) as x approaches infinity is 2. The constant terms and those without the highest power of x become insignificant, leaving only the term with x to the highest power in the numerator and denominator.
How does the arctangent function behave as x approaches infinity or negative infinity?
-As x approaches infinity, the arctangent of x approaches 90 degrees or pi/2 radians. As x approaches negative infinity, the arctangent of x approaches -90 degrees or -pi/2 radians. This behavior reflects the fact that the tangent function approaches infinity and negative infinity as x approaches these values from the left and right, respectively.
What is the limit of e^(-x) as x approaches infinity?
-The limit of e^(-x) as x approaches infinity is 0. As x becomes very large, the value of e raised to a negative power becomes very small, approaching zero because the base of the exponent, e, is a positive number greater than 1.
Outlines
📚 Understanding Limits at Infinity
This paragraph introduces the concept of limits at infinity, specifically focusing on the behavior of the function 1/x as x approaches both positive and negative infinity. It explains that the value approaches zero when the denominator is large, regardless of the sign of x. The paragraph also discusses the graphical representation of 1/x, highlighting the presence of a vertical asymptote at x=0 and a horizontal asymptote at y=0. The general theorem that any function of the form 1/x^r will approach zero as x approaches infinity is presented, providing a foundational understanding for further analysis of limits.
🔢 Analyzing Bottom Heavy Functions
The second paragraph delves into the behavior of 'bottom heavy' functions, where the degree of the denominator is greater than the numerator. It demonstrates that such functions will approach zero as x approaches infinity, using the example of 8/(3x+4). The process of multiplying the numerator and denominator by 1/x to find the limit is explained, and the conclusion that the limit is zero is reached. The paragraph reinforces the concept by discussing the limit of 8x-5/(2x+3), where the degrees of the numerator and denominator are equal, and the limit is found by simply dividing the coefficients, resulting in a limit of 4.
🔍 Examining Higher Degree Functions
This paragraph examines functions where the numerator and denominator have the same degree, using the example of 5 - 7x^3 / (3x + 5x^3 + 9). It explains that higher degree terms in the numerator become insignificant as x increases, and the limit can be approximated by simplifying the expression. The step-by-step process of applying the limit as x approaches infinity to each term in the fraction is outlined, leading to the conclusion that the limit is -7/5. The paragraph also addresses the limit of the square root of (16x^2 - 8) / (2x - 5), showing that the limit is 2, achieved by a similar process of simplification and applying the limit.
🌟 Limits of Trigonometric and Exponential Functions
The final paragraph discusses the limits of the arctangent and exponential functions as x approaches infinity and negative infinity. It explains that the arctangent of infinity approaches 90 degrees or pi/2 radians and that the arctangent of negative infinity approaches -90 degrees or -pi/2 radians. The paragraph also addresses the limit of e^(-x) as x approaches infinity, which is zero, and provides a brief overview of the graph of e^x, noting its horizontal asymptote at y=0. The understanding of these limits is crucial for comprehending the behavior of more complex functions at extreme values.
Mindmap
Keywords
💡Limits at Infinity
💡Asymptote
💡Rational Functions
💡Polynomial Long Division
💡Inverse Trigonometric Functions
💡Exponential Functions
💡Direct Substitution
💡Trigonometric Functions
💡Degree of a Polynomial
💡Horizontal Asymptote
💡Vertical Asymptote
Highlights
The limit of 1/x as x approaches infinity is zero, indicating that large denominators yield small values.
The limit of 1/x as x approaches negative infinity is also zero, but approached from the left side.
The graph of 1/x has a vertical asymptote at x=0 and a horizontal asymptote at y=0.
The limit of 1/x^2 as x approaches infinity is 0, demonstrating that higher powers in the denominator lead to a quicker approach to zero.
The general theorem states that the limit of 1/x^r as x approaches infinity is always 0 for any positive exponent r.
For the function 8/(3x+4), the limit as x approaches infinity is 0, showing that bottom-heavy functions yield a limit of zero if the denominator's degree is greater than the numerator's.
The limit of (8x-5)/(2x+3) as x approaches infinity is 4, highlighting that when the degrees of the numerator and denominator are equal, the limit is the ratio of the coefficients.
The limit of (5-7x^3)/(3x+5x^3+9) as x approaches infinity is -7/5, demonstrating that insignificant terms can be ignored when the variable's exponent is the highest.
The limit of the square root of (16x^2-8)/ (2x-5) as x approaches infinity is 2, showing that only the most significant terms matter for large values of x.
The limit of the square root of (9x^6-x^2)/ (3x^3+1) as x approaches infinity is 1, illustrating that terms with lower significance cancel out.
The limit of the square root of (9x^2+x-3x) as x approaches infinity is 1/6, showing the technique of direct substitution with large numbers for estimation.
The arctangent function approaches pi/2 (90 degrees) as x approaches positive infinity and approaches -pi/2 (-90 degrees) as x approaches negative infinity.
e^(-x) approaches 0 as x approaches infinity, and also approaches 0 as x approaches negative infinity.
The function e^(-x) has a horizontal asymptote of y=0, indicating that the value of the function approaches zero for large values of x.
The limit of a function can be found by simplifying and applying the limit to each term separately, as demonstrated with the function (5-7x^3)/(3x+5x^3+9).
The use of direct substitution with large values of x can provide an estimation of the limit, as shown with the function (9x^2+x-3x).
The technique of multiplying the numerator and denominator by the conjugate can be used to simplify and find the limit of a function, as illustrated with the function (9x^2+x-3x).
Transcripts
Browse More Related Video

Business Calculus - Math 1329 - Section 1.5 (and 1.6) - Limits and Continuity

Limit examples (part 2) | Limits | Differential Calculus | Khan Academy

Calculus: Limits at Infinity-Algebraic

Math 133 Lecture 2 6

Finding limits at infinity using squeeze theorem | Squeeze or Sandwich Theorem - Calculus
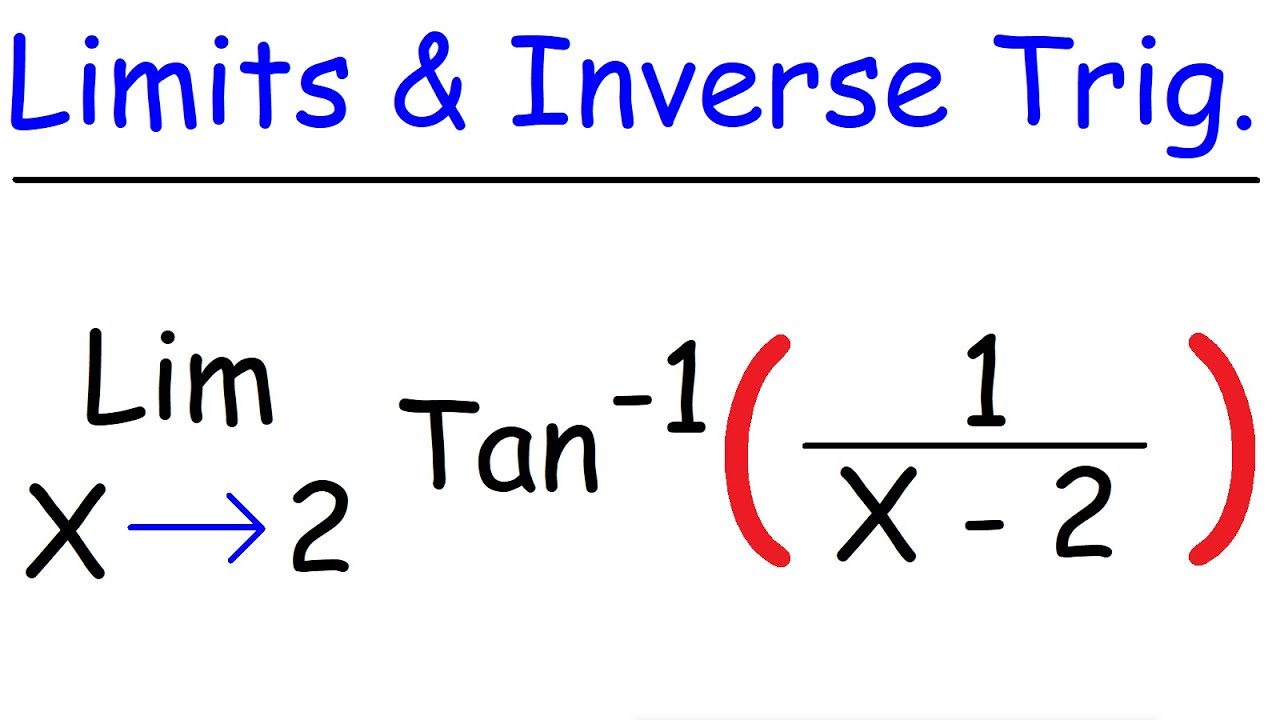
Limits of Inverse Trigonometric Functions | Calculus
5.0 / 5 (0 votes)
Thanks for rating: