AP Physics 1 - Horizontal Spring Block Oscillators
TLDRIn this educational video, Dan Fullerton delves into the principles of horizontal spring-block oscillators, focusing on the relationship between frequency, angular frequency, and period. He guides viewers through the process of determining the minima, maxima, and zeros of displacement, velocity, and acceleration for a spring-block oscillator. Fullerton also explores the total energy of an object in simple harmonic motion and illustrates how to sketch graphs of kinetic and potential energies. The video is enriched with sample problems and a detailed analysis of energy conservation and transfer in a frictionless environment, providing a comprehensive understanding of the topic.
Takeaways
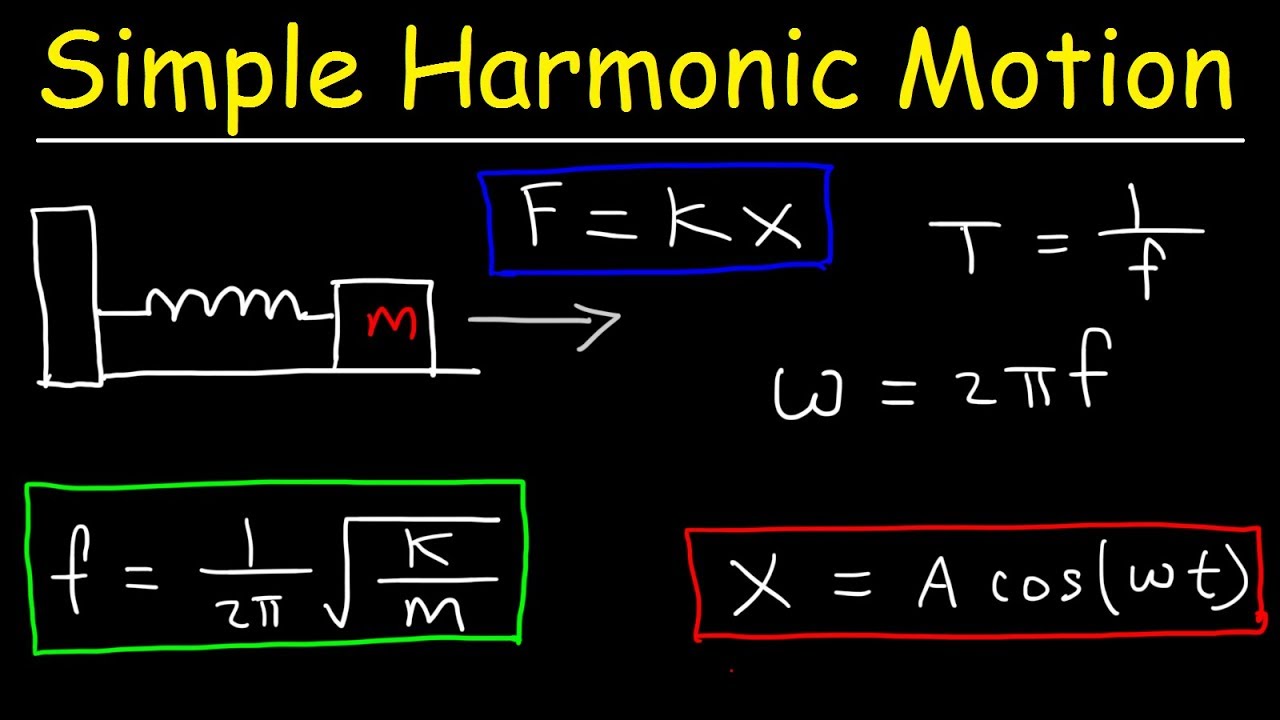
- 📚 The spring-block oscillator is a system consisting of a mass M on a frictionless surface attached to a vertical wall by an ideal spring with spring constant K.
- 📈 The angular frequency (ω) of the oscillator's motion is given by the square root of K/m.
- 🔄 The period (T) of oscillation is independent of the magnitude of displacement and is calculated as 2π√(m/K).
- 📊 To rank spring-block oscillators by period, use the formula T = 2π√(m/K) and compare the calculated periods for different systems.
- 🌐 At the equilibrium position, the block has maximum speed and zero potential energy, while at maximum displacement, the block has zero speed and maximum potential energy.
- 🔄 The total energy in a spring-block oscillator system remains constant throughout its motion, transitioning between kinetic and potential forms.
- 📊 The velocity of the block is maximum at the equilibrium position and zero at the points of maximum displacement.
- ⚖️ The force exerted by the spring on the block is zero at equilibrium and maximum (in restoring force) at points of maximum displacement.
- 📈 The acceleration of the block is zero at equilibrium and maximum (in magnitude) at the points of maximum displacement due to the force exerted by the spring.
- 🔄 In a real-world scenario, energy is lost to non-conservative forces like friction, leading to a decrease in amplitude over time, known as damping.
- 🔢 To find the speed of the block at various positions, use the relationship between total energy, potential energy at maximum displacement, and kinetic energy at equilibrium.
Q & A
What is a horizontal spring block oscillator?
-A horizontal spring block oscillator is a system consisting of a block of mass M sitting on a frictionless surface and attached to a vertical wall by an ideal spring with spring constant K. The block is displaced from its equilibrium position and then allowed to oscillate back and forth.
How is the angular frequency of a spring block oscillator determined?
-The angular frequency (Omega) of a spring block oscillator is determined by the mass of the block and the spring constant. It is calculated as the square root of the spring constant divided by the mass (Omega = √(K/M)).
What is the formula to calculate the period of oscillation for a spring block oscillator?
-The period of oscillation (T) for a spring block oscillator is calculated using the formula T = 2π√(M/K), where M is the mass of the block and K is the spring constant.
Does the period of oscillation depend on the magnitude of the displacement?
-No, the period of oscillation does not depend on the magnitude of the displacement. It only depends on the mass of the block and the spring constant.
In a spring block oscillator, what happens to the energy of the system when it is undergoing simple harmonic motion?
-In an ideal spring block oscillator undergoing simple harmonic motion, the total energy of the system remains constant. There is a continual transfer of energy between kinetic energy and elastic potential energy, but the total energy does not change.
At what points during the oscillation does the block have maximum speed and maximum acceleration?
-The block has maximum speed at its equilibrium position (zero displacement) and maximum acceleration at its maximum amplitude positions (X and -X), where it momentarily has zero velocity.
How does the force on the block and its acceleration change at different points during the oscillation?
-At the equilibrium position (zero displacement), there is no force and hence no acceleration on the block. At the maximum displacement points (X and -X), the force is maximum (according to Hooke's law), providing the maximum acceleration (in opposite directions).
What is the relationship between the displacement, velocity, and acceleration of the block during its oscillation?
-The displacement, velocity, and acceleration of the block are sinusoidally related. At maximum displacement, the velocity is zero, and the acceleration is maximum (in magnitude). At the equilibrium position, the velocity is maximum, and the acceleration is zero. The acceleration graph is a mirror image of the force graph.
What is the total energy of the system in the given example with a 5 kg block and a 2000 N/m spring?
-For the given example, the total energy of the system is approximately 5 Joules, calculated using the formula (1/2)KX^2 for the elastic potential energy at maximum displacement and equating it to the kinetic energy at the equilibrium position.
How can you find the speed of the block at a specific position during its oscillation?
-The speed of the block at a specific position can be found using the total energy of the system and the formula for kinetic energy (KE = (1/2)mv^2). The speed at any position is given by v = √(2 * total_energy / m), where m is the mass of the block.
What is the net force on the block at the equilibrium position and at a position of 25 cm displacement?
-At the equilibrium position, the net force on the block is zero because there is no displacement and no spring force. At a displacement of 25 cm (or 0.25 m), the net force is calculated using Hooke's law as F = -K * X, which results in a force of -10 N (negative indicates direction).
At which position does the kinetic energy equal the elastic potential energy in the spring?
-The kinetic energy equals the elastic potential energy at a displacement X where X = √(total_energy / (1/2 * K)). In the example provided, this displacement is approximately 0.35 meters or 35 cm.
Outlines
📚 Introduction to Spring Block Oscillators
This paragraph introduces the concept of horizontal spring block oscillators and outlines the objectives of the lesson. The speaker, Dan Fullerton, explains that the focus will be on applying the relationship between frequency, angular frequency, and period, identifying minima, maxima, and zeros of displacement, velocity, and acceleration for a spring block oscillator, determining the total energy of an object undergoing simple harmonic motion, and sketching graphs of kinetic and potential energies as functions of time or displacement. The paragraph also describes the setup of a spring block oscillator, consisting of a block of mass M on a frictionless surface, attached to a vertical wall by an ideal spring with spring constant K. The angular frequency of the block's oscillation is derived from its mass and the spring constant, and from this, the period of oscillation is calculated. A sample problem is presented to calculate the period, frequency, and angular frequency for a 5 kg block attached to a 2000 N/m spring, displaced by 8 cm from its equilibrium position.
📈 Ranking Oscillators by Period and Energy Analysis
In this paragraph, the speaker discusses how to rank different spring block oscillators by their period of oscillation. A method is provided for determining the period using the formula T = 2π√(M/K). The speaker then poses a challenge to the audience to find the periods for four different systems labeled A, B, C, and D. After a pause for the audience, the speaker returns to rank the systems from longest to shortest period. The paragraph continues with an in-depth analysis of energy in a spring block oscillator, emphasizing that the total energy remains constant during simple harmonic motion, with a continuous transfer between kinetic and potential energy. The speaker describes the energy dynamics at the equilibrium position and at maximum amplitude positions, highlighting that at equilibrium, all energy is kinetic, while at maximum amplitude, all energy is potential. A graphical representation of position, velocity, potential energy, and force is used to illustrate these concepts.
📊 Detailed Analysis of Displacement, Velocity, and Energy
This paragraph delves deeper into the analysis of a horizontal spring block oscillator, focusing on displacement, velocity, stored elastic potential energy, kinetic energy, net force, and acceleration. The speaker explains how these quantities vary at different points during the oscillation cycle. At points of maximum displacement (B and C), the velocity is zero, and the energy is entirely potential, while at the equilibrium position (A), the energy is all kinetic. The speaker then addresses a sample problem involving a 2 kg block attached to a spring with a force constant of 20 N/m, stretched to a displacement of 50 cm. The spring constant is calculated using Hooke's law, and the total energy is determined using the displacement and spring constant. The speed of the block at equilibrium and at various positions is calculated, demonstrating how velocity changes with position. The acceleration at the equilibrium point and at a displacement of 50 cm is also calculated, using Newton's second law and Hooke's law. The net force on the block at equilibrium and at a displacement of 25 cm is determined. Finally, the speaker finds the position where the kinetic energy equals the elastic potential energy of the spring, highlighting that this point is not midway between the equilibrium position and the maximum displacement position.
🎓 Conclusion and Further Resources
The speaker concludes the lesson on simple harmonic motion in horizontal spring block oscillators by summarizing the key points discussed. The importance of understanding the conservation of energy, the relationship between kinetic and potential energy, and the dynamics of displacement, velocity, and acceleration is emphasized. The speaker encourages the audience to seek further help or ask questions on the topic and wishes everyone a great day. The paragraph ends with a prompt for additional resources on the topic, directing the audience to a website for more information.
Mindmap
Keywords
💡Spring Block Oscillator
💡Angular Frequency
💡Period
💡Frequency
💡Displacement
💡Simple Harmonic Motion
💡Kinetic Energy
💡Potential Energy
💡Acceleration
💡Hooke's Law
💡Damping
Highlights
Introduction to horizontal spring block oscillators and their application in understanding simple harmonic motion.
Objectives include applying the relationship between frequency, angular frequency, and period, as well as identifying minima, maxima, and zeros of displacement, velocity, and acceleration for a spring-block oscillator.
Explanation of how to determine the angular frequency of a block's oscillation from its mass and spring constant, and how to calculate the period of oscillation.
Sample problem: A 5 kg block attached to a 2000 N/m spring, displaced 8 cm from equilibrium, is used to illustrate the calculation of period, frequency, and angular frequency.
Ranking spring-block oscillators based on their period, highlighting that the period depends only on the mass of the block and the spring constant, not the magnitude of displacement.
Discussion on the conservation of total energy in a spring-block oscillator undergoing simple harmonic motion, with a continuous transfer between kinetic and potential energy.
Graphical representation of the spring-block oscillator's position, velocity, potential energy, kinetic energy, force, and acceleration at various points in its oscillation cycle.
Analysis of the force and acceleration on the block at different displacements, emphasizing that force and acceleration are directly related and mirror each other's graph.
Extended sample problem: A 2 kg block attached to a spring with a force of 20 N stretches to a 50 cm displacement, used to find the spring constant and total energy.
Explanation of how to calculate the block's speed at equilibrium and at various positions using the conservation of total energy and Hooke's law.
Detailed calculation of the block's acceleration at different positions, demonstrating the relationship between force, mass, and acceleration according to Newton's second law.
Investigation of the net force on the block at equilibrium and at various displacements, reinforcing the principles of Hooke's law and Newtonian mechanics.
Identification of the position where kinetic energy equals potential energy in the spring, showing that this does not occur halfway between equilibrium and maximum displacement.
Conclusion summarizing the key concepts of simple harmonic motion in horizontal spring-block oscillators and directing readers to further resources for additional help.
Transcripts
Browse More Related Video

Simple Harmonic Motion - Complete Review of the Mass-Spring System

AP Physics 1 - Vertical Spring Block Oscillators

AP Physics 1 - Spring Combinations

2023 AP Physics 1 Free Response #1

Simple harmonic motion and angular frequency [IB Physics SL/HL]
How To Solve Simple Harmonic Motion Problems In Physics
5.0 / 5 (0 votes)
Thanks for rating: