2023 AP Physics 1 Free Response #1

Allen Tsao The STEM Coach
13 May 202307:23
EducationalLearning
32 Likes 10 Comments

TLDRThis video script tackles the 2023 AP Physics 1 free response questions, offering solutions with a promise of corrections in the comments. It delves into a cart-spring system's harmonic motion, explaining energy conservation with kinetic and potential energy graphs. The script also addresses the effect of adding a block to the system, calculating frequency changes and illustrating how the total energy remains constant, with kinetic and potential energy distribution shifting accordingly.

Takeaways
  • 📚 The transcript discusses the 2023 AP Physics 1 free response questions, with the speaker providing their best guess solutions since official solutions are not released yet.
  • 🔍 The speaker mentions that any mistakes in their solutions will be corrected in a pinned comment in the video.
  • 🚂 The script describes a physics problem involving a cart and a spring on a horizontal surface, where the system oscillates between two positions with negligible frictional forces.
  • 📉 The kinetic and potential energy of the system are graphed, with the x-intercept and y-intercept having the same values, which is explained by the conservation of energy.
  • 🔄 The conservation of energy principle is emphasized, where the total energy remains constant at all times, with the energy being entirely kinetic or potential at the intercepts.
  • 📌 The x-intercept represents when all the energy is kinetic, and the y-intercept represents when all the energy is potential, both totaling four joules in the example given.
  • 🔢 The speaker calculates the frequency of oscillation before and after a block is dropped onto the cart, using the formula for the period of a simple harmonic oscillator.
  • ⏰ The frequency of oscillation after the block is added is found to be half of the original frequency, indicating a longer period due to the increased mass.
  • 📈 The graph of kinetic versus potential energy remains identical after the block is added, explained by the fact that the total energy of the system does not change at the moment the block is dropped.
  • 📐 The script includes a sketch of the kinetic energy for the system consisting only of the cart and the spring after the block is added, showing how the energy is divided between the cart and the block.
  • 🤔 The speaker provides a detailed explanation of the energy distribution between the cart and the block, highlighting that the block will have three times the kinetic energy of the cart due to its greater mass.
Q & A

  • What type of motion is described in the 2023 AP Physics 1 released free response question involving a cart and a spring?

    -The motion described is harmonic motion, where the system consisting of the cart and the spring oscillates between positions.

  • Why are the x-intercept and y-intercept values the same on the graph of kinetic energy versus potential energy for the cart-spring system?

    -The x-intercept and y-intercept values are the same because energy is conserved in the system. At the x-intercept, all the energy is kinetic, and at the y-intercept, all the energy is potential, both amounting to four joules.

  • What is the significance of the block being dropped onto the cart in the scenario described?

    -The block being dropped onto the cart increases the mass of the system, affecting the frequency of oscillation. The block sticks to the cart, and they continue to oscillate together.

  • How does the frequency of oscillation change after the block is dropped onto the cart?

    -The frequency of oscillation decreases after the block is dropped onto the cart because the period of oscillation increases due to the added mass.

  • What is the relationship between the frequency of oscillation before and after the block is dropped onto the cart?

    -The frequency after the block is dropped (F2) is half the frequency before the block was dropped (F1), as the period is longer with the additional mass.

  • Why are the graphs of kinetic energy versus potential energy identical for the cart-spring system before and after the block is dropped?

    -The graphs are identical because the total energy of the system remains the same, and the collision of the block with the cart does not change the potential energy at the moment of impact.

  • What does the kinetic energy of the cart-spring system represent at the maximum point after the block is dropped?

    -At the maximum point, the kinetic energy is split between the cart and the block, with the block having three times the energy of the cart due to its greater mass.

  • How is the kinetic energy distributed between the cart and the block after the block is dropped onto the cart?

    -The kinetic energy is distributed such that one joule corresponds to the kinetic energy of the cart, and the remaining three joules correspond to the kinetic energy of the block.

  • What is the role of potential energy in the conservation of energy principle as described in the script?

    -Potential energy plays a crucial role in the conservation of energy principle as it converts to kinetic energy and vice versa without any loss in the total energy of the system.

  • Why is there no loss in energy in the cart-spring system as described in the script?

    -There is no loss in energy because no external work is being done on the system, and the energy transitions between kinetic and potential forms without dissipation.

Outlines
00:00
🔍 Analyzing the 2023 AP Physics 1 Free Response Questions

This paragraph discusses the 2023 AP Physics 1 exam's free response questions, noting the absence of official solutions until after scores are released. The speaker provides their own solutions, promising corrections in the comments if needed. The scenario involves a cart on a horizontal surface attached to a spring, oscillating due to the spring's force. The kinetic and potential energy graph is explained, with the x-intercept and y-intercept values being identical due to energy conservation. The speaker clarifies the meaning of these intercepts in the context of the system's energy states.

05:02
📉 Kinetic and Potential Energy Graphs Post-Block Attachment

The second paragraph delves into the effects of attaching a block to the cart during its oscillation. The kinetic and potential energy graph remains unchanged after the block is attached, which is explained by the conservation of the system's total energy at the moment of attachment. The block's addition does not alter the spring's potential energy, hence the total energy and the shape of the energy graph remain the same. The paragraph also addresses the change in frequency due to the increased mass, calculating the new frequency as half of the original, reflecting a longer period and a lower frequency due to the additional mass.

Mindmap
Keywords
💡AP Physics 1
AP Physics 1 is a college-level course and examination offered by the College Board. It is designed to introduce students to the foundational principles of physics, including kinematics, energy, and momentum. In the video, the script discusses the released free response questions from the 2023 AP Physics 1 exam, indicating the educational context of the video.
💡Harmonic Motion
Harmonic motion refers to the motion of an object when it is subject to restoring forces that are proportional to the displacement from its equilibrium position. The video script describes a cart and spring system that oscillates in a harmonic manner, with the cart moving back and forth due to the spring's force.
💡Kinetic Energy
Kinetic energy is the energy an object possesses due to its motion, calculated as one-half the mass of the object times the square of its velocity (1/2 mv^2). In the video, the script explains how the kinetic energy of the cart-spring system is represented on a graph and how it changes as the cart oscillates.
💡Potential Energy
Potential energy is the stored energy of an object due to its position in a force field, such as a spring. In the context of the video, potential energy is discussed in relation to the spring's ability to store energy when compressed or stretched, and how it is converted to kinetic energy as the cart moves.
💡Conservation of Energy
The principle of conservation of energy states that the total energy of an isolated system remains constant over time. The video script mentions this principle to explain why the total energy represented by the sum of kinetic and potential energy remains the same throughout the cart-spring system's oscillation.
💡X-intercept and Y-intercept
In the context of graphs, the x-intercept is the point where a line crosses the x-axis, and the y-intercept is where it crosses the y-axis. The script uses these terms to describe the points on the kinetic energy vs. potential energy graph where one form of energy is zero and the other is at its maximum, illustrating the conservation of energy.
💡Frequency of Oscillation
The frequency of oscillation is the number of oscillations that occur per unit time, typically measured in hertz (Hz). The video discusses how the frequency of the cart-spring system changes after a block is added to the cart, affecting its mass and the period of oscillation.
💡Period
The period of an oscillating system is the time taken for one complete cycle of the motion. It is the reciprocal of the frequency. The script explains how the period of oscillation is related to the mass and spring constant, and how it changes when additional mass is added to the system.
💡Spring Constant (k)
The spring constant, denoted as 'k', is a measure of the stiffness of a spring. It is defined as the force needed to stretch or compress the spring by one unit of length. In the video, the spring constant is used in the formula to calculate the period of oscillation for the cart-spring system.
💡Momentum
While not explicitly mentioned in the script, the concept of momentum is implied in the discussion of the block being dropped onto the cart. Momentum is the product of an object's mass and velocity and is conserved in a closed system. The addition of the block to the cart would affect the system's momentum during the collision.
💡Collision
A collision is an event in which two or more bodies exert forces on each other for a very short period of time. In the video, the script describes a collision where a block sticks to the cart, becoming part of the oscillating system and changing its dynamics.
Highlights

The 2023 AP Physics 1 released free response questions are discussed without official solutions, as those are released after scores.

A cart on a horizontal surface is attracted to a spring, oscillating between positions in a harmonic motion when released.

The kinetic and potential energy graph shows the system's energy conservation with the same x and y intercept values, both at 4 Joules.

The x-intercept represents when all energy is kinetic (4 Joules) and the y-intercept when all energy is potential (4 Joules), due to energy conservation.

No energy loss occurs as no external work is being done on the system, maintaining energy conservation.

When the cart is momentarily at rest, a block is dropped under it and sticks, changing the system's dynamics.

The block-cart system continues to oscillate with increased mass, affecting the frequency of oscillation.

The frequency of oscillation before and after the block is dropped is calculated, showing a decrease in frequency with added mass.

The kinetic and potential energy graph remains identical after the block is dropped, indicating no change in total system energy.

The block's addition does not change the spring's potential energy, maintaining the system's total energy.

After the block is dropped, the cart-spring system's kinetic energy is redistributed, with the block having 3x the energy of the cart.

The kinetic energy graph for the cart-spring system after the block is dropped is sketched, showing the energy distribution between the cart and block.

The maximum kinetic energy is split into 1 Joule for the cart and 3 Joules for the block, reflecting the mass ratio.

The video provides a step-by-step explanation of the physics principles and calculations involved in the problem.

The importance of energy conservation and its implications on the system's behavior is emphasized throughout the explanation.

The video aims to clarify the concepts of kinetic and potential energy, frequency of oscillation, and the effects of mass on these properties.

The problem-solving approach demonstrates the application of physics principles to analyze and understand the system's behavior.

Transcripts

Browse More Related Video

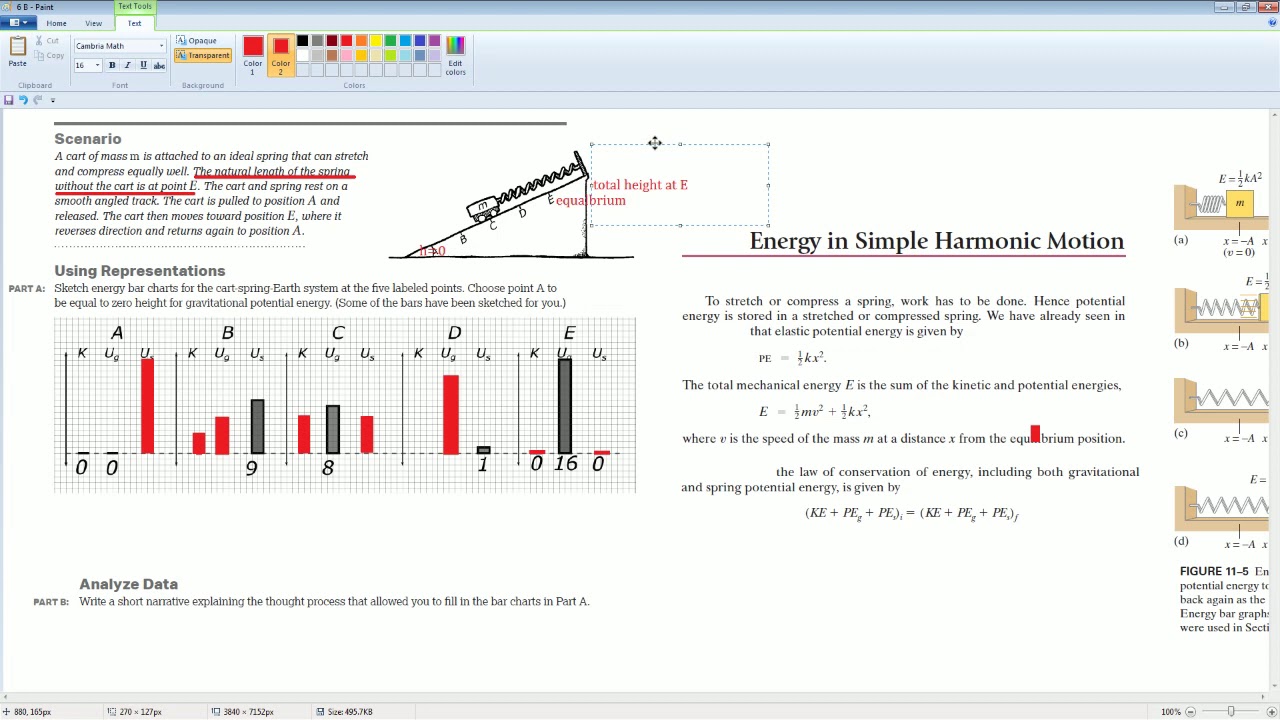
AP Physics Workbook 6.B Simple Harmonic Motion and Energy Review

'AP Physics 2023 Exam Solutions|Q1. PART C ( i ) | Complete Step-by-Step Answers and Explanations"

'AP Physics 2023 Exam Solutions|Q1. PART C ( ii ) | Complete Step-by-Step Answers and Explanations"

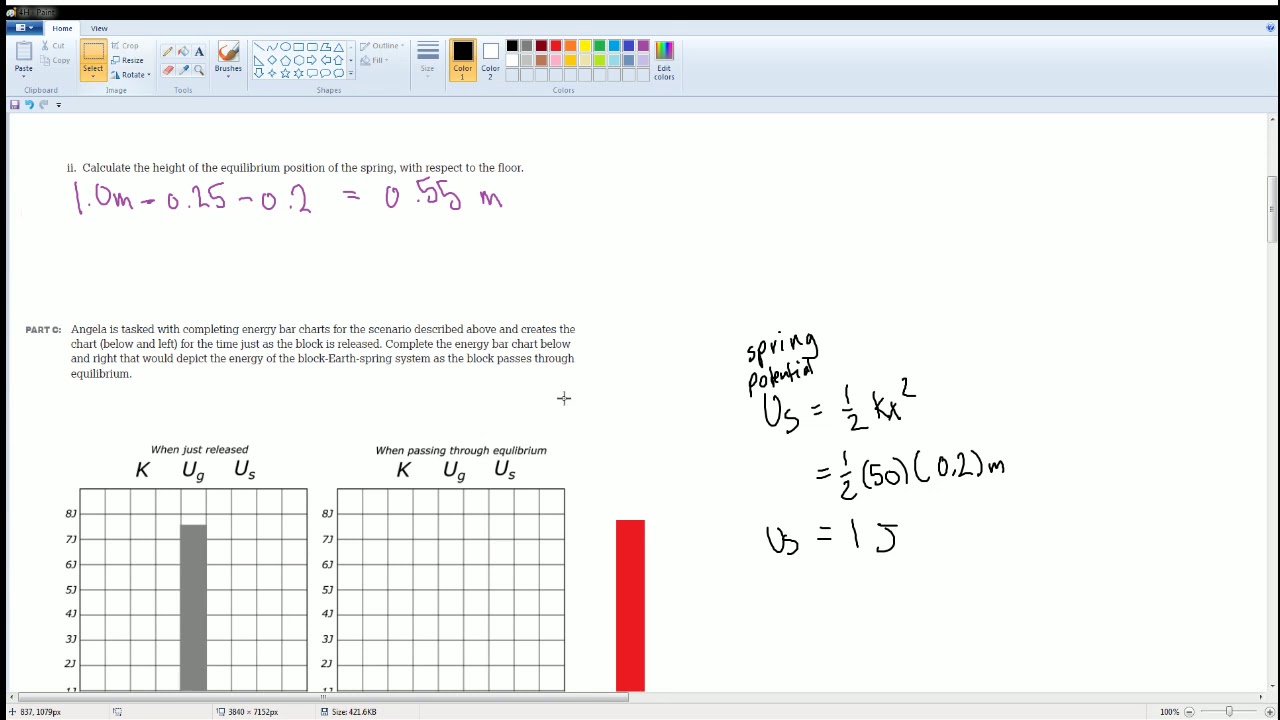
AP Physics Workbook 4.H Potential Energy and Choice of Zero

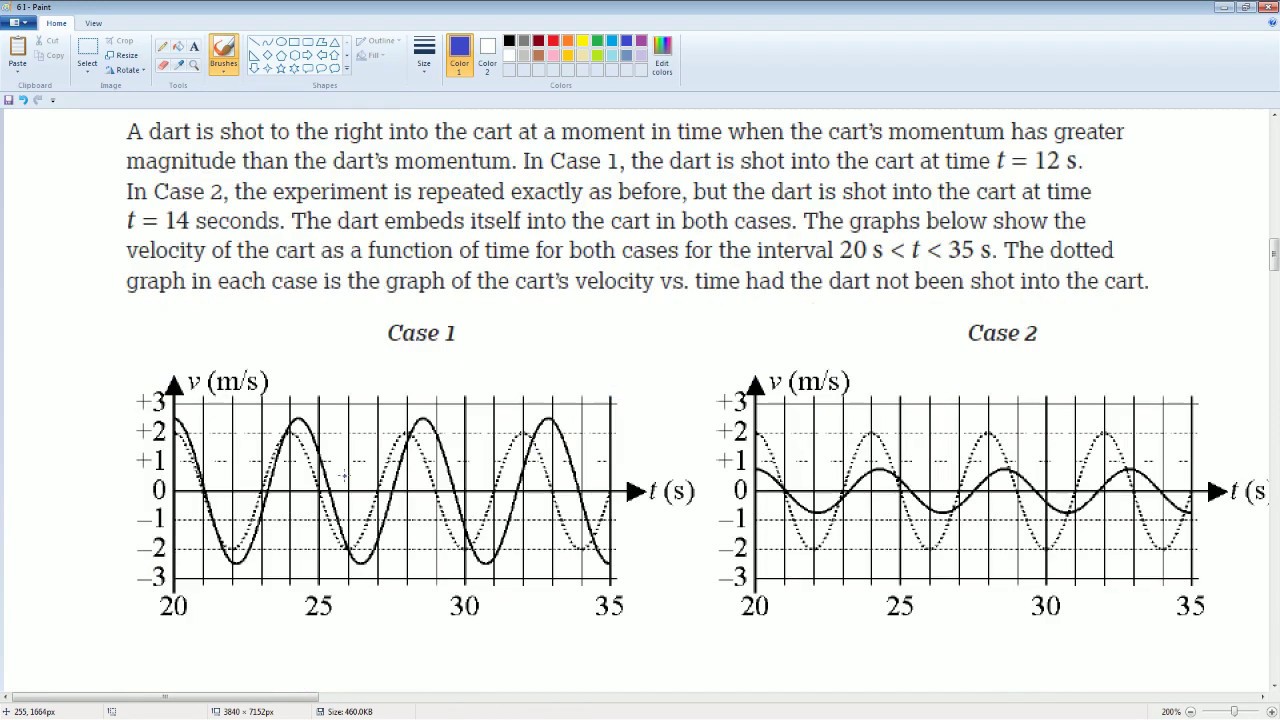
AP Physics Workbook 6.I Changing Mass and Period of a Mass Spring SYstem

AP Physics 1 - Horizontal Spring Block Oscillators

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
AP PhysicsExam AnalysisFree ResponseHarmonic MotionEnergy ConservationSpring SystemKinetic EnergyPotential EnergyPhysics PrinciplesEducational Content