Simple harmonic motion and angular frequency [IB Physics SL/HL]

OSC

11 Jan 202413:07

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video script delves into the concept of simple harmonic motion (SHM), a fundamental topic in physics. It explains SHM through examples like springs and pendulums, emphasizing the proportionality and opposite direction of acceleration to displacement. The script introduces angular frequency, measured in radians per second, and its relationship with SHM. It further explores the linearization of SHM's acceleration-displacement graph, the significance of the gradient, and equations relating frequency, period, and angular frequency. The video also covers deriving the spring constant and acceleration due to gravity using the period of oscillation, offering a practical approach to understanding these principles.

Takeaways

🔄 Simple harmonic motion (SHM) is not just repetitive motion; it has a specific definition.
🔧 Examples of SHM include a mass on a frictionless surface with springs and a pendulum.
⚖️ SHM features include acceleration proportional to displacement and opposite in direction.
📏 The key equation for SHM is acceleration = -ω²x, where ω is the angular frequency.
📐 Angular frequency (ω) is measured in radians per second.
📉 Linearization of equations helps in recognizing the linear form y = mx + c.
🧮 For SHM, the graph of acceleration vs. displacement is a straight line through the origin with a negative slope.
🔍 Angular frequency (ω) can be determined as the square root of the gradient from a linearized graph.
⏲️ The period (T) of oscillation is related to frequency (f) and angular frequency (ω) through the equations T = 1/f and ω = 2π/T.
📊 Linearizing the equation for the period of a mass on a spring or a pendulum can help determine constants like the spring constant (k) or gravitational acceleration (g).

Q & A

What is simple harmonic motion?
-Simple harmonic motion (SHM) is a type of periodic motion where an object oscillates back and forth through an equilibrium position, and the acceleration of the object is directly proportional to its displacement from the equilibrium position and is directed towards that position.
Can you give an example of simple harmonic motion?
-A common example of simple harmonic motion is a mass attached to a frictionless spring. When the mass is displaced and released, it oscillates back and forth around its equilibrium position. Another example is a simple pendulum that swings back and forth under the influence of gravity.
What is the relationship between acceleration and displacement in simple harmonic motion?
-In simple harmonic motion, acceleration is proportional to displacement but in the opposite direction. This relationship can be expressed as a = -ω²x, where a is the acceleration, ω (omega) is the angular frequency, and x is the displacement from the equilibrium position.
What does the equation a = -ω²x represent in simple harmonic motion?
-The equation a = -ω²x is the mathematical representation of simple harmonic motion, showing that the acceleration (a) is directly proportional to the negative of the displacement (x) from the equilibrium position. The constant ω² represents the angular frequency squared, which determines the rate of oscillation.
What are the units of angular frequency?
-Angular frequency (ω) is measured in radians per second (rad/s). It describes how quickly an object moves through its oscillatory cycle in terms of angular displacement.
How can we determine the angular frequency from a graph of acceleration versus displacement?
-When graphing acceleration versus displacement in simple harmonic motion, the slope (gradient) of the line is equal to -ω². By taking the square root of the absolute value of the gradient, we can determine the angular frequency (ω) of the motion.
What is the relationship between frequency and period in oscillatory motion?
-Frequency (f) and period (T) are inversely related in oscillatory motion. The period (T) is the time it takes to complete one full cycle, and the frequency (f) is the number of cycles completed per second. Mathematically, T = 1/f.
How is the angular frequency (ω) related to the period (T) of oscillation?
-The angular frequency (ω) is related to the period (T) by the formula ω = 2π/T. This equation shows that angular frequency is proportional to the reciprocal of the period and describes how many radians per second the system oscillates.
How can we use the period of a mass-spring system to find the spring constant (k)?
-The period (T) of a mass-spring system is given by the formula T = 2π√(m/k), where m is the mass and k is the spring constant. By rearranging the equation and using the period from experimental data, we can determine the spring constant k as k = 4π²/(slope), where slope is from a graph of T² versus mass.
How can the acceleration due to gravity (g) be determined from a pendulum experiment?
-In a pendulum experiment, the period (T) is related to the length (L) of the pendulum and the acceleration due to gravity (g) by the formula T = 2π√(L/g). By plotting T² against L and finding the slope, the acceleration due to gravity can be calculated using g = 4π²/(slope).

Outlines

00:00

🔄 Introduction to Simple Harmonic Motion

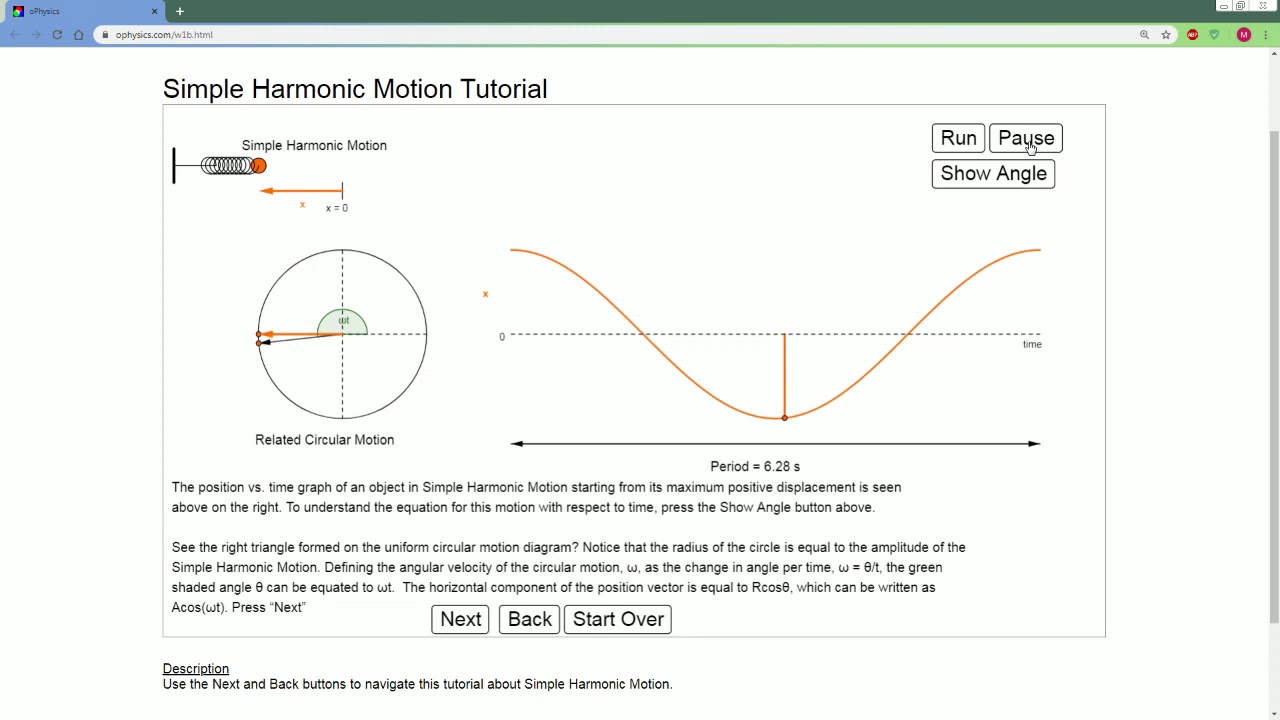
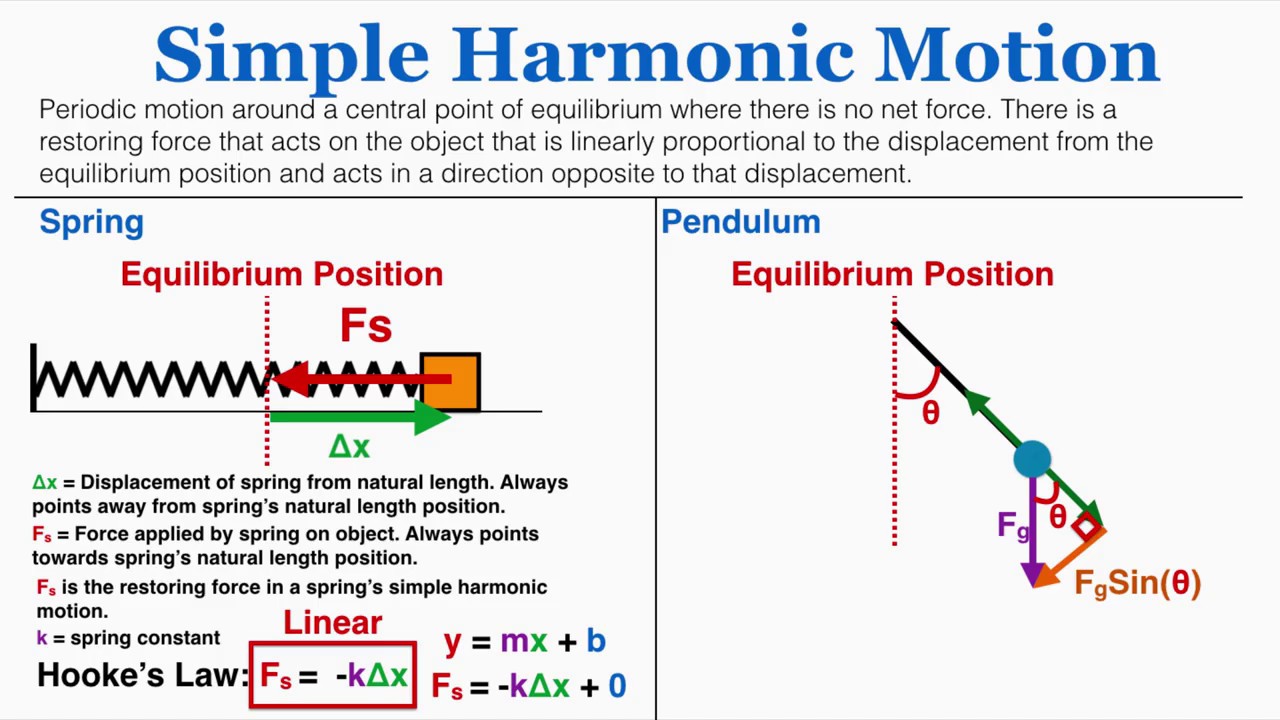
This paragraph introduces the topic of simple harmonic motion (SHM) and angular frequency. It emphasizes the need for a specific definition of SHM and provides examples such as a mass on a frictionless surface with springs and a pendulum. The key characteristic of SHM is that the acceleration is proportional to the displacement but in the opposite direction.

05:00

📉 Graphing and Linearization of SHM Equations

The second paragraph explains the concept of linearization in the context of SHM. It details how to graph acceleration versus displacement and identifies the importance of recognizing the equation in the form y = mx + C. The paragraph also discusses the significance of the gradient and Y-intercept in understanding the relationship between acceleration and displacement.

10:02

📊 Exploring the Relationship between Frequency and Period

This paragraph delves into the relationship between frequency and period. It introduces the formula for angular frequency (omega) and its relation to the period (T). The paragraph explains the units involved and how to derive various forms of the equation to find the period, frequency, or angular frequency based on given information.

🔍 Graphing T^2 vs. M for a Mass-Spring System

In this section, the script discusses how to linearize the equation for the period of a mass on a spring by graphing T^2 versus mass (M). It describes how the gradient of the resulting straight-line graph can be used to determine the spring constant (K). This method involves manipulating the equation to fit the linear form y = mx + C.

⏳ Pendulum Period and Length Relationship

The final paragraph explains the relationship between the period of a pendulum and its length. Similar to the mass-spring system, it involves linearizing the equation by graphing T^2 versus length (L). The gradient of this graph corresponds to a value that includes the acceleration due to gravity (g), allowing for its determination through experimentation.

Mindmap

Keywords

💡Simple Harmonic Motion (SHM)

Simple Harmonic Motion is a type of periodic motion where the restoring force is directly proportional to the displacement and acts in the direction opposite to that of displacement. In the video, examples such as a mass on a spring and a pendulum are used to illustrate SHM, highlighting that the acceleration is proportional and opposite to the displacement.

💡Angular Frequency

Angular frequency, denoted by the symbol ω (omega), measures how quickly an object undergoes circular motion or oscillation, expressed in radians per second. The video explains that angular frequency is an important concept in SHM and introduces the formula for angular frequency as ω = 2π/T, where T is the period.

💡Restoring Force

Restoring force is the force that brings a system back to its equilibrium position. In SHM, this force is directly proportional to the displacement and acts in the opposite direction. The video describes how the restoring force for a mass on a spring or a pendulum leads to oscillatory motion.

💡Displacement

Displacement in the context of SHM refers to how far the system is from its equilibrium position at any given point. The video uses the example of pulling a mass on a spring to a maximum displacement and observing how it oscillates back and forth through the equilibrium position.

💡Acceleration

Acceleration in SHM is proportional to the displacement but in the opposite direction, described by the equation a = -ω²x. The video emphasizes that understanding the relationship between acceleration and displacement is crucial for analyzing SHM.

💡Linearization

Linearization involves transforming a non-linear relationship into a linear one to simplify analysis. The video demonstrates this technique by squaring equations related to SHM to create straight-line graphs, facilitating the calculation of key parameters like angular frequency.

💡Period

The period (T) is the time it takes for one complete cycle of oscillation in SHM. The video explains the relationship between period and frequency, noting that T = 1/f and showing how the period can be derived from experimental data.

💡Frequency

Frequency (f) is the number of complete oscillations per unit time, measured in Hertz (Hz). The video details the inverse relationship between period and frequency, f = 1/T, and connects it to angular frequency through the formula ω = 2πf.

💡Hooke's Law

Hooke's Law states that the force exerted by a spring is proportional to its displacement, given by F = -kx, where k is the spring constant. The video references Hooke's Law when discussing the spring constant and how it influences the period of a mass-spring system.

💡Spring Constant

The spring constant (k) measures the stiffness of a spring, defined in Hooke's Law as the ratio of force to displacement. In the video, the spring constant is used to derive the period of oscillation for a mass-spring system, showing its importance in determining the system's behavior.

Highlights

Introduction to simple harmonic motion (SHM) and its definition.

Examples of SHM, including a mass on a frictionless surface with springs and a pendulum.

The key feature of SHM where acceleration is proportional and in the opposite direction to displacement.

The formal equation for SHM, relating acceleration to displacement with angular frequency squared.

Units of angular frequency are radians per second, denoted by the symbol Omega.

Exploring the concept of linearization in the context of SHM graphs.

The relationship between the gradient of the linearized graph and the angular frequency.

Key equations connecting frequency, period, and angular frequency.

The significance of the units for period, frequency, and angular frequency in SHM.

Equation for the period of oscillation of a mass on a spring.

Method to linearize the equation for the period of a mass on a spring by squaring the period.

The concept of using the gradient of a graph to determine the spring constant.

Equation for the period of a pendulum and its relation to the length of the pendulum.

Technique to linearize the pendulum's period equation by squaring the period.

The experimental application of graphing T^2 versus L to determine the acceleration due to gravity.

The importance of understanding SHM for practical applications in physics.

Transcripts

Browse More Related Video

AP Physics 1 - Simple Harmonic Motion

AP Physics Lecture on Simple Harmonic Motion. Watch this before 6.C

Rotational Motion: An Explanation, Angular Displacement, Velocity and Acceleration

Simple Harmonic Motion - Complete Review of the Mass-Spring System

01 - Oscillations And Simple Harmonic Motion, Part 1 (Physics Tutor)

Simple Harmonic Motion - IB Physics