AP Physics Workbook 6.G Period and Amplitude for SHM
TLDRThe video script explores the principles of simple harmonic motion (SHM) through a pendulum demonstration. It discusses the relationship between the pendulum's amplitude (aptitude) and its period, highlighting a debate between two students, Angelica and Carlos. Angelica argues that a larger amplitude increases the period due to the greater distance traveled, while Carlos contends that a higher amplitude results in a faster average speed and thus a shorter period. The script uses equations and physical concepts, such as mechanical energy and force, to explain the dynamics of SHM and ultimately reveals that for small angle oscillations, the period of a pendulum is independent of its amplitude and depends solely on the length of the string and gravitational force.
Takeaways
- 🎥 The video demonstrates the conservation of mechanical energy in a physical scenario involving the release of an object.
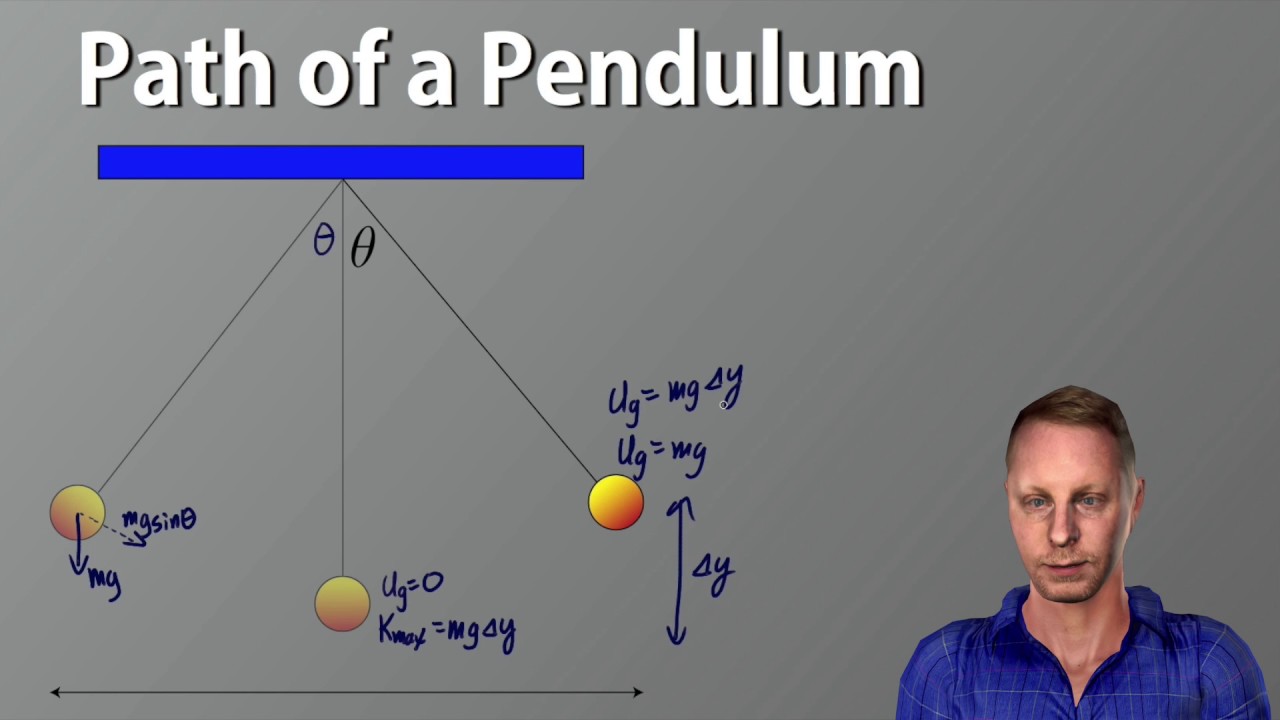
- 📐 The period of a pendulum is derived from the equation T = 2π√(L/g), highlighting that it depends on the length of the string and gravitational acceleration, not the mass.
- 🤔 Angelica argues that a greater amplitude leads to a longer period, as the amplitude is in the numerator of the period equation, directly affecting the outcome.
- 🚀 Carlos contends that a larger amplitude results in a greater average speed during the cycle, leading to a shorter period due to the increased velocity.
- 📊 The lab experiment shows that increasing the amplitude from 5 to 7 has a minimal effect on the period, supporting the idea that small changes in amplitude do not significantly alter the period.
- 🔄 The total distance traveled in one cycle of a sine wave is four times the amplitude, which is a fundamental concept in understanding the motion of a pendulum.
- 🌐 The force exerted on the ball increases with the amplitude, as the component of force tangent to the pendulum's path is proportional to the sine of the pendulum's angle.
- 🌐 The potential energy in the ball-Earth system increases with the amplitude, as more energy is converted into kinetic energy during the pendulum's motion.
- 🔄 The lab results confirm that the energy in the system oscillates between potential and kinetic, but the total energy remains constant.
- 🌟 For small angle oscillations, the period of a pendulum is independent of its initial angle displacement, meaning the amplitude does not affect the period in such cases.
- 📚 The key takeaway is that the period remains constant when the pendulum undergoes small angle oscillations, as it is determined by the length of the string and gravitational pull, not the amplitude.
Q & A
What is the main topic of the video?
-The main topic of the video is the concept of simple harmonic motion, specifically focusing on the period of a pendulum and how it relates to the pendulum's amplitude and other factors.
How does the scenario with the lecturer and the ball demonstrate the conservation of mechanical energy?
-The lecturer demonstrates the conservation of mechanical energy by releasing a ball at zero speed, expecting it to return to touch his chin due to the conservation of energy. The ball's potential energy at the highest point is converted to kinetic energy as it swings down, and this energy conversion continues throughout the pendulum's motion.
What is the equation for the period of a pendulum derived from?
-The equation for the period of a pendulum is derived from the relationship between the maximum velocity (V_max) and the amplitude (a) of the pendulum's motion, which is V_max = 2πaptitude/T. By solving for T (the period), we get T = 2πa/V_max.
How does the amplitude (aptitude) affect the period of a pendulum according to Angelica's argument?
-According to Angelica's argument, a greater amplitude (aptitude) means a larger period because the distance the ball travels in one cycle depends on the amplitude. As the amplitude increases, the period also increases to maintain the balance in the equation relating them.
What is Carlos's argument regarding the relationship between the amplitude and the period of a pendulum?
-Carlos argues that a greater amplitude should result in a shorter period because the ball will have a greater average speed during its cycle. A higher average speed implies less time is needed to complete the cycle.
How does the force exerted on the ball affect its speed in the context of a pendulum with a greater amplitude?
-A greater amplitude means the pendulum is lifted to a higher initial height. When the pendulum is released, the higher gravitational potential energy is converted into kinetic energy, resulting in a faster speed due to the increased potential energy being converted.
What is the relationship between the potential and kinetic energy in a pendulum system?
-In a pendulum system, the potential energy is converted into kinetic energy as the pendulum swings from the highest point to the lowest point. Conversely, as it swings back up, the kinetic energy is converted back into potential energy. The total mechanical energy in the system remains constant throughout these conversions.
How does the period of a pendulum change with the amplitude if the oscillations are small?
-With small angle oscillations, the period of a pendulum does not depend on the amplitude. Instead, it is independent of the initial angle displacement, meaning that the period remains the same regardless of the amplitude for small oscillations.
What factors determine the period of a pendulum?
-The period of a pendulum is determined by the length of the string and the gravitational pull (acceleration due to gravity). It is independent of the mass of the ball and the amplitude for small angle oscillations.
What was the experimental observation regarding the period of the pendulum at different amplitudes?
-The experimental observation showed that the period of the pendulum did not change significantly when the amplitude was increased from 5 to 7. This suggests that for small amplitudes, the period is relatively constant.
How does the concept of mechanical energy conservation apply to the pendulum's motion?
-The conservation of mechanical energy applies to the pendulum's motion as the total energy in the system (the sum of potential and kinetic energy) remains constant throughout the pendulum's swing. The potential energy at the highest point is maximum, and as the pendulum descends, this energy is converted into kinetic energy, which is maximum at the lowest point.
Outlines
📚 Introduction to Simple Harmonic Motion
The paragraph introduces the concept of simple harmonic motion (SHM) and the specific scenario of a pendulum. It sets the stage for the discussion by mentioning the conservation of mechanical energy and the potential consequences of releasing an object at zero speed. The video aims to visually demonstrate the principles of SHM using a YouTube video, emphasizing the importance of paying attention to the conservation of energy and the expected outcomes based on the initial conditions. The paragraph also introduces a debate between two students, Angelica and Carlos, about the relationship between the period of oscillation and the amplitude (aptitude) of the pendulum's swing, highlighting different perspectives on how the period might change with varying amplitudes.
📐 Derivation and Implications of the Period Equation
This paragraph delves into the mathematical derivation of the period equation for a pendulum undergoing SHM. It explains how the equation is derived using the maximum velocity (V Max) and the amplitude (aptitude) of the swing. The paragraph clarifies that the total distance traveled in one cycle of a sine wave is four times the amplitude, and how the average velocity is related to the amplitude and period. It then connects the equation to the students' arguments, showing how an increase in amplitude leads to an increase in the period, and how a greater average speed would theoretically result in a shorter period. The paragraph also discusses the relationship between the pendulum's height, gravitational potential energy, and the resulting kinetic energy, providing a deeper understanding of the forces and energy transformations at play.
🧪 Lab Experiments and Energy Analysis
The final paragraph focuses on practical lab experiments that validate the theoretical concepts discussed earlier. It describes the setup of a pendulum with a period timer to test the students' hypotheses about the period's relationship with amplitude. The results from varying the amplitude show that the period remains relatively consistent, challenging the initial assumptions made by the students. The paragraph also explores the forces and energy involved in the pendulum's motion, explaining how the force exerted on the ball changes with the amplitude and how this affects the speed and energy transformation within the system. The energy analysis is visualized through energy graphs, illustrating the oscillation between potential and kinetic energy. The paragraph concludes with a clarification that, for small angle oscillations, the period of a pendulum is independent of its amplitude, relying instead on the length of the string and the gravitational force.
Mindmap
Keywords
💡Conservation of Mechanical Energy
💡Simple Harmonic Motion (SHM)
💡Amplitude
💡Period
💡Average Speed
💡Velocity
💡Force
💡Acceleration
💡Gravitational Potential Energy
💡Kinetic Energy
💡Energy Conservation
Highlights
The demonstration of the conservation of mechanical energy with a released object and its potential to touch the chin without causing harm.
The importance of releasing the object at zero speed for the conservation of mechanical energy demonstration.
The argument between Angelica and Carlos on the relationship between the period of oscillation and the amplitude (aptitude) of the motion.
Derivation of the equation for the period of a pendulum using the maximum velocity (V Max) and amplitude (aptitude).
Explanation of how the total distance traveled in one cycle of a sine wave is four times the amplitude.
The relationship between average velocity and the maximum velocity in the context of a pendulum's cycle.
Support for Angelica's reasoning that a greater aptitude results in a larger period due to its position in the numerator of the equation.
Support for Carlos's reasoning that a greater velocity implies a smaller period, also based on its position in the equation.
The impact of a greater aptitude on the pendulum's angle and the resulting increase in the force exerted on the ball.
The explanation of how mechanical energy in the ball-earth system is converted from potential to kinetic energy due to an increase in height and potential energy.
The experimental verification of the period's independence from the amplitude when the pendulum undergoes small angle oscillations.
The demonstration that the period of a pendulum is dependent on the length of the string and gravitational pull, not the mass of the ball.
The conclusion that the period remains the same for small angle oscillations regardless of the initial angle displacement.
The practical application of the concepts in a lab setting, showing the effect of changing the amplitude on the period and the forces involved.
The visual representation of energy conservation in a pendulum system, with potential and kinetic energy oscillating between each other while the total remains constant.
The final answer and explanation that the period of a pendulum remains unchanged with an increase in aptitude under the assumption of small angle oscillations.
Transcripts
Browse More Related Video
AP Physics 1 - Pendulums

AP Physics 1 review of Waves and Harmonic motion | Physics | Khan Academy
Amplitude, Time period, Frequency and the Wavelength: Understand these terms in Hindi

8.01x - Lect 10 - Hooke's Law, Springs, Pendulums, Simple Harmonic Motion

The Conical Pendulum

Pendulums | Oscillations and mechanical waves | Physics | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: