AP Physics 1 - Pendulums

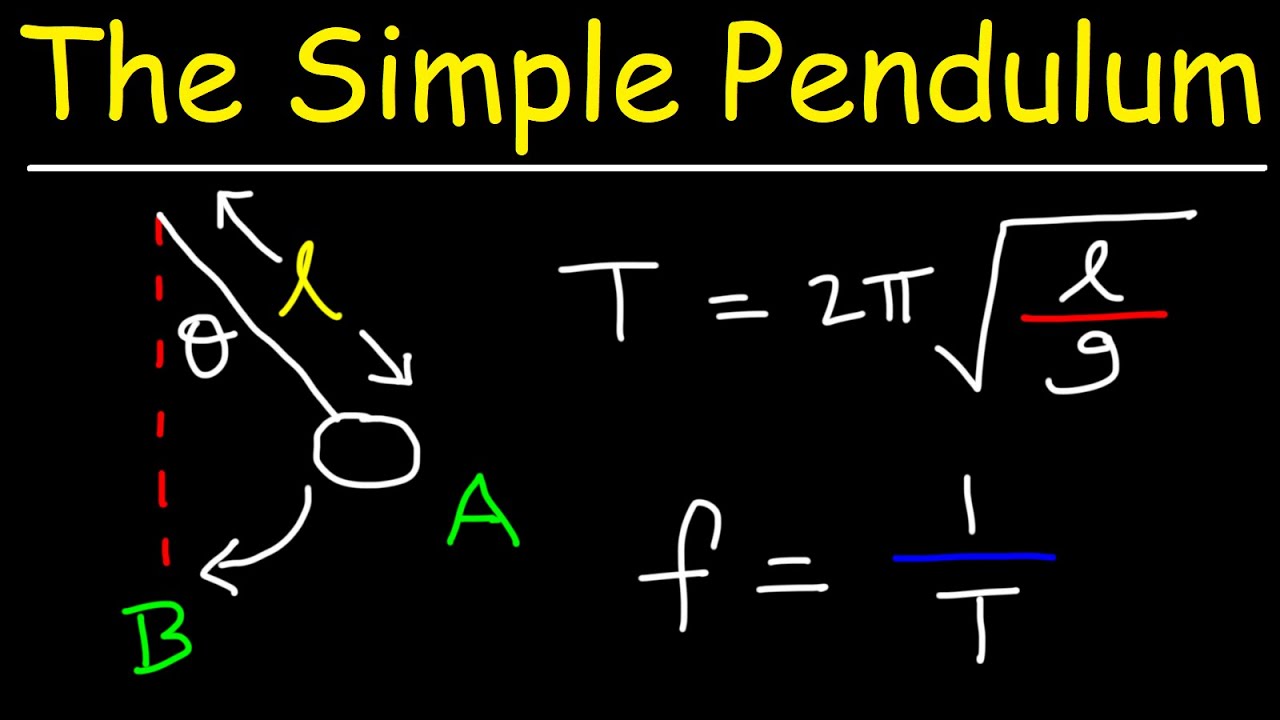
This paragraph introduces the concept of an ideal pendulum, which is a model for simple harmonic motion. It explains that an ideal pendulum consists of a mass M attached to a light string that swings without friction around a vertical equilibrium position. The energy of the pendulum continuously transfers between gravitational potential energy at higher points and kinetic energy at lower points. The restoring force is provided by gravity. The angular frequency for small angles of theta is given by the formula Omega = sqrt(G/L), where G is the acceleration due to gravity and L is the length of the pendulum. The period of the pendulum is derived from the angular frequency, which is 2π sqrt(L/G). It is noted that the period depends only on the length of the string and the acceleration due to gravity, and not on the mass at the end of the string.

This paragraph delves into the specifics of a grandfather clock, which is designed such that each swing or half-period of the pendulum takes one second. Using the formula for the period of a pendulum, the length of the pendulum is calculated to be approximately one meter, given that the period is two seconds (one second for each half-period). The discussion then moves to the scenario of placing a grandfather clock on the moon, where the acceleration due to gravity is 1/6 that of Earth's. The period of the pendulum on the moon is calculated to be 4.9 seconds, highlighting how the period changes due to variations in gravitational acceleration.

This paragraph addresses the task of ranking pendulums of uniform mass density by frequency, from highest to lowest. It is explained that since mass does not affect the period of a pendulum, the only factor to consider is the length of the pendulum. Longer pendulums have longer periods, and shorter pendulums have shorter periods. Thus, the ranking would be from shortest to longest pendulum based on their lengths.

This paragraph explores the energy transformation and velocity of a pendulum at its lowest point. At the lowest point, all the gravitational potential energy has been converted into kinetic energy, which is at its maximum. The energy conservation law is used to calculate the maximum velocity of the pendulum at the lowest point using the formula V = sqrt(2GL(1 - cos(theta))). The relationship between the change in height (Delta Y) and the maximum velocity is also discussed, emphasizing the conservation of mechanical energy throughout the pendulum's swing.

This paragraph examines the energy graph of a pendulum, illustrating the relationship between kinetic energy, gravitational potential energy, and the position of the mass along its path. The total mechanical energy remains constant throughout the pendulum's motion. The graph shows total energy as a constant line, with kinetic and potential energy changing positions based on the pendulum's location. The sum of gravitational potential energy and kinetic energy at any point equals the total mechanical energy, reinforcing the principle of conservation of energy in the ideal pendulum's motion.

This paragraph discusses the effects of changing the mass and length of a pendulum on its period. It is emphasized that the mass does not affect the period, but the length does. Using the formula for the period of an ideal pendulum, it is shown that if the mass is tripled and the length is quadrupled, the new period will be twice the original period. This is because the period is proportional to the square root of the length and independent of the mass.

This paragraph calculates the maximum speed of a pendulum of length 20 centimeters with a mass of one kilogram, displaced at an angle of 10 degrees from the vertical. Using the conservation of energy principle and the formula for maximum velocity at the lowest point of a pendulum's swing, the speed is determined to be approximately 0.24 meters per second. The calculation takes into account the acceleration due to gravity and the cosine of the angle, highlighting the practical application of the concepts discussed.