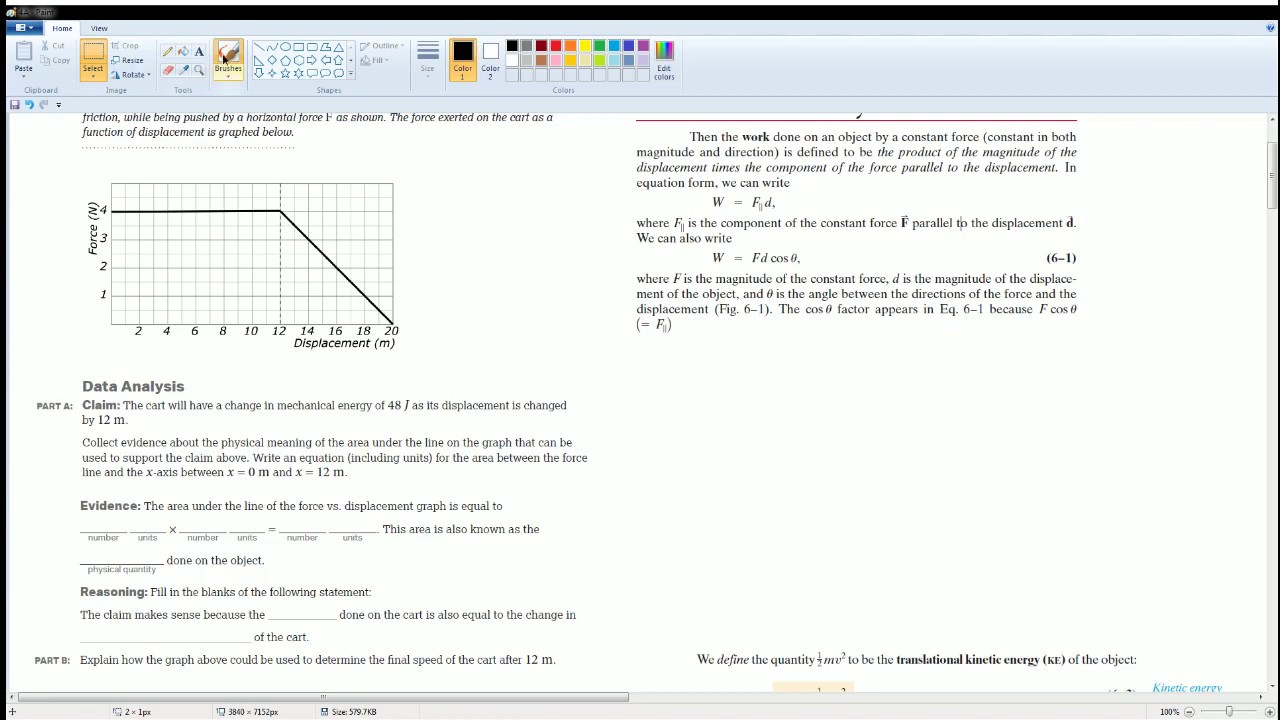
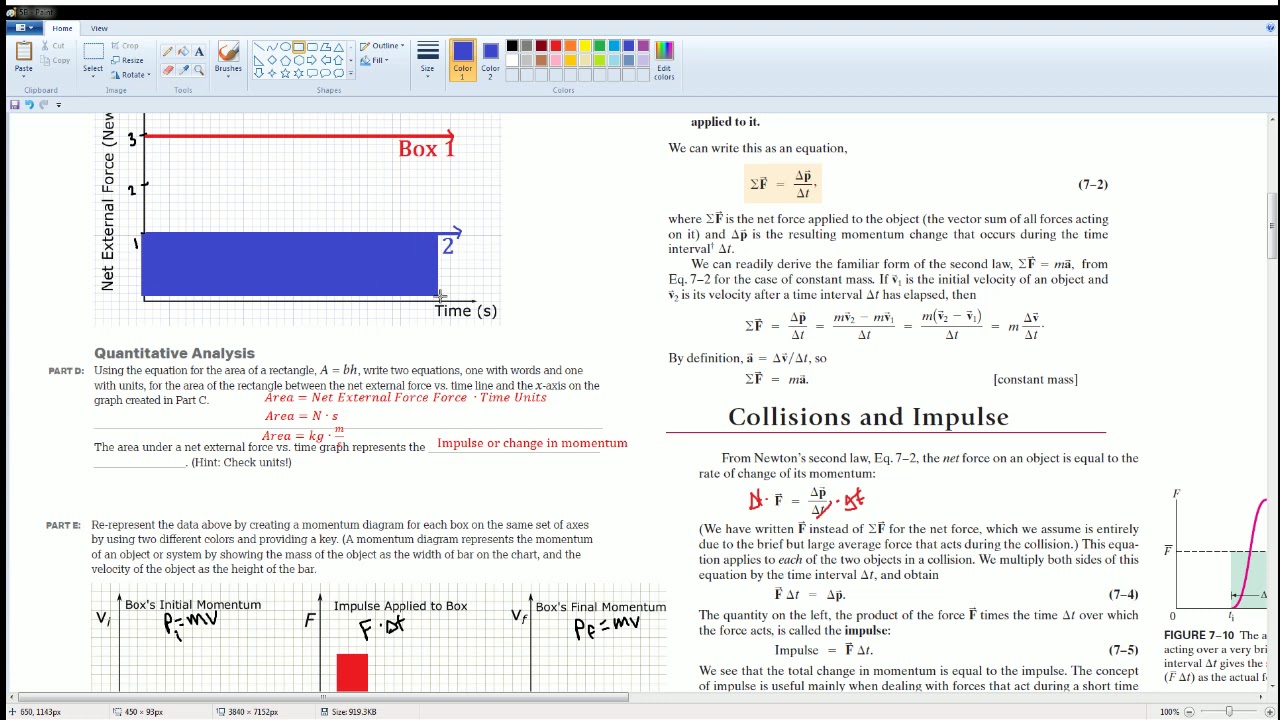
AP Physics Workbook 4.E Comparisons of Work by Identical Forces
TLDRThis video script delves into the concept of work and energy in the context of physics, specifically focusing on the comparison of work done by identical forces under different conditions. It presents a scenario where a car is pushed up a smooth incline, examining two cases where the force is applied either parallel to the incline or horizontally. The script explains why the final velocity of the car is greater in the first case using the principles of work and energy, highlighting the impact of the force's component along the incline and the cosine theta factor. The explanation is supplemented with detailed mathematical derivations and a clear breakdown of the forces involved, ultimately reinforcing the understanding of work, energy, and their relationship in physical systems.
Takeaways
- 📚 The concept of work in physics is defined as the product of the force applied and the displacement in the direction of the force.
- 🔄 When the force is not parallel to the displacement (as in the case of an incline), the work done is calculated using the formula W = F * cos(theta) * D, where theta is the angle between the force and the displacement.
- 🚗 In the given scenario, a car is pushed up an incline in two different cases, with the force F either applied parallel to the incline or horizontally.
- 📈 The velocity of the car is greater in case A (force applied parallel to the incline) than in case B (force applied horizontally) due to the component of the force being more effective in case A.
- 🎯 Newton's second law (F = ma) is used to determine that the acceleration in case B is less than in case A, as the effective force (F * cos(theta)) is smaller.
- 🌟 The final velocity of the car depends on the acceleration, which in turn depends on the effective force applied, leading to a higher final velocity in case A.
- 🔋 The work done on the car can also be described in terms of energy transfer, where work equals the change in kinetic energy.
- 📊 The work-energy principle is used to derive the equations for final velocities in both cases, with the work done (W) being equal to the change in kinetic energy (1/2 * m * v^2).
- 🔧 The components of the gravitational force (mg) on the incline are considered, with mg * sin(theta) being opposite to the direction of motion, and mg * cos(theta) being perpendicular to the motion.
- 📐 Trigonometric relationships are crucial in understanding the force components on an incline, with the angles and the cosine function playing a key role in the calculations.
- 📝 The script provides a detailed explanation of the physics concepts involved in comparing the work done and the resulting velocities in two different scenarios of force application on an incline.
Q & A
What is the main topic of the AP Physics workbook section discussed in the transcript?
-The main topic is the comparison of work done by identical forces in two different scenarios involving a car on a smooth incline.
What are the two cases presented in the scenario?
-Case A involves pushing the car up the incline with a force F applied parallel to the incline, while in Case B, the force F is applied horizontally.
How does the smooth incline's angle, theta, affect the work done in both cases?
-The angle theta introduces a cosine theta component when the force is not applied parallel to the incline, affecting the work calculation as W = F_parallel * D * cos(theta).
Why is the final velocity in Case A greater than in Case B?
-The final velocity in Case A is greater because the force F is applied more effectively along the incline, resulting in greater acceleration and more work done compared to Case B where the force is applied horizontally.
What is the definition of work given in the transcript?
-Work is defined as the product of the magnitude of the displacement and the force parallel to the displacement, which is given by W = F_parallel * D.
How does Newton's second law relate to the acceleration in both cases?
-According to Newton's second law, the acceleration is calculated by the net force divided by the mass (a = F_net / M). In Case B, the net force is less due to the cosine theta component, resulting in less acceleration compared to Case A.
What is the relationship between the work done and the change in energy?
-The work done on an object is equal to the change in its energy. This can be expressed as W = ΔE, where W is the work and ΔE is the change in energy.
How is the work equation expressed in terms of force and distance?
-The work equation can be expressed as W = F_parallel * D, where F_parallel is the force component parallel to the direction of displacement.
What is the significance of the trigonometric function cosine in the work calculation?
-The cosine function is used to determine the component of the force that is parallel to the incline. When the force is not applied directly along the incline, the cosine of the angle theta is used to calculate the effective force component.
How does the force component F cosine theta affect the work done in Case B?
-In Case B, the force is applied horizontally, so only a component of the force, F cosine theta, contributes to pushing the car up the incline. This results in less work done compared to Case A where the force is applied directly along the incline.
What is the mathematical relationship between the final velocities in Case A and Case B?
-The final velocity in Case A (Vf_a) is greater than in Case B (Vf_b) because the net force acting on the car in Case B is less due to the F cosine theta component, leading to a smaller change in kinetic energy and thus a lower final velocity.
Outlines
📚 Introduction to Work and Energy in AP Physics
This paragraph introduces the concept of work and energy in the context of AP Physics, focusing on the work done by forces on an object, specifically a car, in different scenarios. It explains the difference in the final velocities of the car when the force is applied parallel to the incline versus when it's applied horizontally. The explanation involves the definition of work as the product of the force's magnitude and the displacement in the direction of the force, introducing the cosine theta factor when the force is not parallel to the displacement. The paragraph also touches on the use of Newton's second law to determine acceleration and the subsequent final velocity, emphasizing that the greater acceleration in case A (force applied along the incline) leads to a higher final velocity compared to case B (force applied horizontally).
🔢 Numerical Calculation and Energy Analysis
The second paragraph delves into the numerical calculation of work and energy, using the work-energy principle to explain the difference in the car's final velocities in the two cases. It introduces the concept of net work (work done by the resultant force) and its relationship with the change in kinetic energy. The explanation includes the breakdown of gravitational force into components (mg sine-theta and mg cosine-theta) and how these components affect the net force acting on the car. The paragraph further clarifies the mathematical relationship between the force applied, the cosine of the incline angle, and the resulting velocities, reinforcing the idea that the cosine theta factor plays a crucial role in determining the car's final velocity.
📈 Understanding Component Forces and Trigonometry
In the final paragraph, the focus is on understanding the component forces and the application of trigonometry in analyzing the problem. It emphasizes the importance of recognizing the angles and the direction of forces involved. The paragraph explains how the force applied to the car can be resolved into components parallel and perpendicular to the incline, and how these components affect the net force and the car's motion. It also provides a geometrical perspective to justify the use of cosine theta in the force equations. The paragraph concludes by encouraging the viewer to practice labeling component forces to better understand and solve such physics problems.
Mindmap
Keywords
💡Work
💡Energy
💡Force
💡Acceleration
💡Incline
💡Velocity
💡Cosine Theta
💡Kinetic Energy
💡Newton's Second Law
💡Components of Force
💡Trigonometry
Highlights
The scenario involves a car being pushed up a smooth incline with different force applications.
In Case A, the force F is applied parallel to the incline, while in Case B, the force is applied horizontally.
The car is pushed from rest up a length L of the incline in both cases.
The velocity of the car in Case A is greater than in Case B due to the force application.
Work is defined as the product of the magnitude of displacement and the force parallel to the displacement.
When the force is not parallel to the ramp, a cosine theta term is introduced to account for the angle.
The work done in Case A is equal to F parallel times D, which is the full force magnitude.
In Case B, the work done is less due to the force being only a component of F (F cosine theta).
Newton's second law is used to determine acceleration, which is less in Case B than in Case A.
The final velocity depends on the acceleration, hence Case A has a greater final velocity.
The energy transferred in the car can be monitored by the work equation, which equates work to the change in energy.
The change in energy is greater in Case A, leading to a higher final velocity due to the greater work done.
The net force in Case B is less due to the force being a fraction of F (F cosine theta).
Cosine theta is between 0 and 1, making the force component in Case B less than the full force in Case A.
The final velocities for Cases A and B are derived from the work and net force equations.
The difference in final velocities is attributed to the cosine theta term, which affects the force component.
Understanding the geometry of the incline and the force components is crucial for solving the problem.
The key takeaway is to label and understand the component forces when dealing with angled surfaces.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: