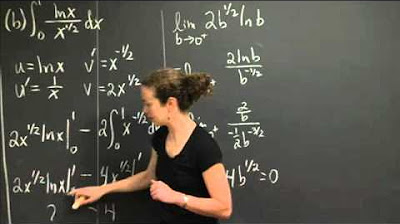Indefinite Integral of 1/x^2
TLDRThis video tutorial explains how to find the indefinite integral of 1/x^2 using the power rule and the importance of rearranging the function to fit the rule's format. It then demonstrates the evaluation of a definite integral of the same function from 1 to 4, highlighting the absence of the constant of integration. The video also addresses the concept of improper integrals, specifically when the function is undefined at points within the integration range, using limits to evaluate such integrals and showing that the improper integral diverges to infinity in this case.
Takeaways
- 📚 The indefinite integral of 1/x^2 is found using the power rule and is expressed as -1/x + C, where C is the constant of integration.
- 🔄 To adapt the power rule for functions in the form of 1/(x^n), rewrite the function to match the rule by flipping the sign of the exponent when moving the variable from the denominator to the numerator.
- 🌟 When evaluating a definite integral, the constant of integration (C) is not included in the calculation.
- 📈 The definite integral of 1/x^2 from 1 to 4 is calculated as [−1/x] evaluated from 1 to 4, resulting in 3/4.
- ⚠️ An improper integral occurs when the range of integration includes a value that makes the function undefined, such as 0 in the case of 1/x^2 from -3 to 3.
- 🎶 To evaluate an improper integral, express it as a limit involving separate integrals from the endpoints to the undefined point, effectively breaking it into two parts.
- 🌐 The graph of 1/x^2 has a vertical asymptote at x=0, which is crucial for understanding the behavior of the function near the undefined point.
- 💥 The improper integral from -3 to 3 of 1/x^2 diverges to infinity because the function approaches infinity as x approaches 0 from both the left and right.
- 📝 When working with improper integrals, it is essential to evaluate the limits carefully and understand that the result can be infinite, indicating a divergence.
- 🔗 Additional resources for learning about indefinite integrals, definite integrals, and improper integrals are available in the description section of the video.
- 🚀 To improve in calculus, practicing various integral problems and watching related educational videos can be beneficial.
Q & A
What is the main topic of the video?
-The main topic of the video is how to find the indefinite integral of 1/x squared and how to evaluate certain types of definite and improper integrals.
What formula is used to find the indefinite integral of x raised to a constant power?
-The formula used is the power rule: ∫(x^n)^c = x^(n*c)/(n*c + 1) + C, where n is a variable, c is a constant, and C is the constant of integration.
How does the process of finding the indefinite integral of 1/x squared differ from the usual power rule?
-The process differs because the function is a rational function and not in the x^n format. The variable x must be moved from the denominator to the numerator, which changes the exponent from positive to negative.
What is the antiderivative of 1/x squared?
-The antiderivative of 1/x squared is -1/x.
How is the definite integral of 1/x squared from 1 to 4 evaluated?
-The definite integral is evaluated by substituting the upper and lower limits of integration into the antiderivative, and then taking the difference: -1/4 - (-1) = 3/4.
Why is the integral of 1/x squared from -3 to 3 considered an improper integral?
-It is considered an improper integral because the function 1/x squared has a vertical asymptote at x=0, which means the function is undefined at that point and within the range of integration.
How is the improper integral of 1/x squared from -3 to 3 evaluated?
-The improper integral is evaluated by breaking it into two parts: the limit as 'a' approaches 0 from the left from -3 to 'a', and the limit as 'b' approaches 0 from the right from 'b' to 3. The result is infinity, indicating that the integral diverges.
What is the significance of the vertical asymptote in the context of improper integrals?
-The vertical asymptote indicates a point where the function is undefined, which can cause the improper integral to diverge to infinity, as was the case with the integral from -3 to 3.
How can one avoid mistakes when dealing with improper integrals?
-One should carefully check if the range of integration includes values that make the function undefined and use the correct method for evaluating improper integrals, which involves taking limits as the integration approaches the points of discontinuity.
What additional resources are provided in the video for further learning?
-The video provides links in the description section for more example problems on finding indefinite integrals, evaluating definite integrals, integrating by u-substitution, and working with other improper integrals.
What is the advice given at the end of the video for those interested in learning more about calculus?
-The advice given is to check out the provided links in the description for more example problems and topics related to calculus, and to subscribe to the channel and turn on notifications for updates on future videos.
Outlines
📚 Finding the Indefinite Integral of 1/x^2
This paragraph introduces the topic of finding the indefinite integral of 1 over x squared. The video explains the process of using the power rule to integrate functions of the form x^n, where n is a variable. It emphasizes the need to rearrange the rational function into a format where x is in the numerator and then apply the power rule. The result is the indefinite integral of 1/x^2, which is -1/x + C. The paragraph also touches on the concept of definite integrals and their evaluation, using the specific example of the integral of 1/x^2 from 1 to 4, highlighting the absence of the constant of integration in definite integrals.
📊 Evaluating Definite Integrals and Improper Integrals
The second paragraph delves into the evaluation of definite integrals and the concept of improper integrals. It discusses the process of evaluating the definite integral of 1/x^2 from -3 to 3, which involves breaking the integral into two parts due to the vertical asymptote at x=0. The paragraph explains that as x approaches zero from the left, the function approaches positive infinity, and as x approaches zero from the right, it also approaches positive infinity. The improper integral diverges to infinity, emphasizing the importance of understanding the domain and asymptotic behavior of functions when integrating.
🎓 Additional Resources and Conclusion
In the final paragraph, the video offers additional resources for viewers interested in further exploring topics such as indefinite integrals, definite integrals, area under curves, integration by u-substitution, and improper integrals. Links to these resources will be provided in the video description for those who wish to enhance their understanding and improve their calculus skills. The video concludes with a reminder to subscribe to the channel and turn on notifications for updates on future videos.
Mindmap
Keywords
💡indefinite integral
💡power rule
💡rational function
💡definite integral
💡constant of integration
💡vertical asymptote
💡improper integral
💡limits
💡antiderivative
💡domain
Highlights
The video discusses finding the indefinite integral of 1/x^2 using the power rule.
The power rule formula for integration is ∫x^n = x^(n+1)/(n+1) + C, where n is a variable and C is the constant of integration.
To apply the power rule, the function must be in the form of x raised to a power; thus, the video demonstrates moving the variable from the denominator to the numerator.
When moving the variable x from the denominator, the exponent's sign changes from positive to negative.
The indefinite integral of 1/x^2 is -1/x + C after applying the power rule and adjusting the exponent.
The video also covers evaluating a definite integral of 1/x^2 from 1 to 4, which is a different process than finding an indefinite integral.
For definite integrals, the constant of integration C is not used.
The antiderivative of 1/x^2 is -1/x, and the definite integral from 1 to 4 is calculated as -1/4 + 1, which equals 3/4.
The video addresses another integral involving 1/x^2 but with different limits of integration from -3 to 3, highlighting the issue of x being undefined at 0.
This improper integral requires a specific evaluation method, involving breaking the integral into two parts and using limits as a and b approach 0 from the left and right, respectively.
The improper integral diverges to infinity because as x approaches 0, 1/x^2 approaches infinity from both the left and right.
The video emphasizes the importance of being cautious when integrating rational functions over ranges that include values making the function undefined.
The video concludes with suggestions for further learning resources, including links in the description for additional example problems and topics in calculus.
The speaker encourages viewers to subscribe to the channel and turn on notifications for updates on future videos.
The video serves as a comprehensive guide for understanding indefinite and definite integrals, power rule application, and the evaluation of improper integrals.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: