Rotational Kinetic Energy | Rolling Without Slipping (AP Physics 1)
TLDRThe video script delves into the concept of 'rolling without slipping,' a fundamental topic in physics that explores the interplay between translational and rotational motion. When an object rolls without slipping, there is no frictional work, thus conserving energy. The script uses examples of an object rolling down an incline and a spinning object falling towards the ground to illustrate this principle. It emphasizes that at the point of contact, the velocity is zero, which is counterintuitive but crucial for understanding the conservation of mechanical energy in these scenarios. The educational content further explains how different objects, such as a solid disc or a block, will have varying speeds at the bottom of a fall due to their distinct moments of inertia. The video also clarifies common misconceptions regarding the forces acting on a rolling object, highlighting the importance of understanding where forces originate for accurate problem-solving. Overall, the script provides a clear explanation of a complex physical phenomenon, making it accessible to students studying for AP physics.
Takeaways
- 📚 The concept of 'rolling without slipping' in physics is important for understanding how objects with both translational and rotational motion behave when there's no friction between the surfaces.
- 🌀 When an object rolls without slipping, the velocity at the point of contact with the ground is zero, which means no work is done by friction, and thus, mechanical energy is conserved.
- 🔄 The special case of rolling without slipping involves both linear and rotational motion, but the sum of velocities at the contact point equals zero due to no slipping.
- ⚙️ An object spinning around its center of mass has a tangential velocity that is zero at the center of mass, which contrasts with the tangential velocity during rotation.
- 📉 The absence of slipping implies that the tangential speed and rotational tangential speed are equal, which is a key factor in energy conservation.
- 🧵 In the example of a string attached to a pulley, the tension in the string (similar to friction on the ground) applies a constant torque, leading to a calculable linear speed of the object after falling a certain distance.
- ⏳ The linear speed of an object rolling down an incline or in freefall can be determined by the conservation of energy principle, splitting the potential energy into linear and rotational kinetic energy components.
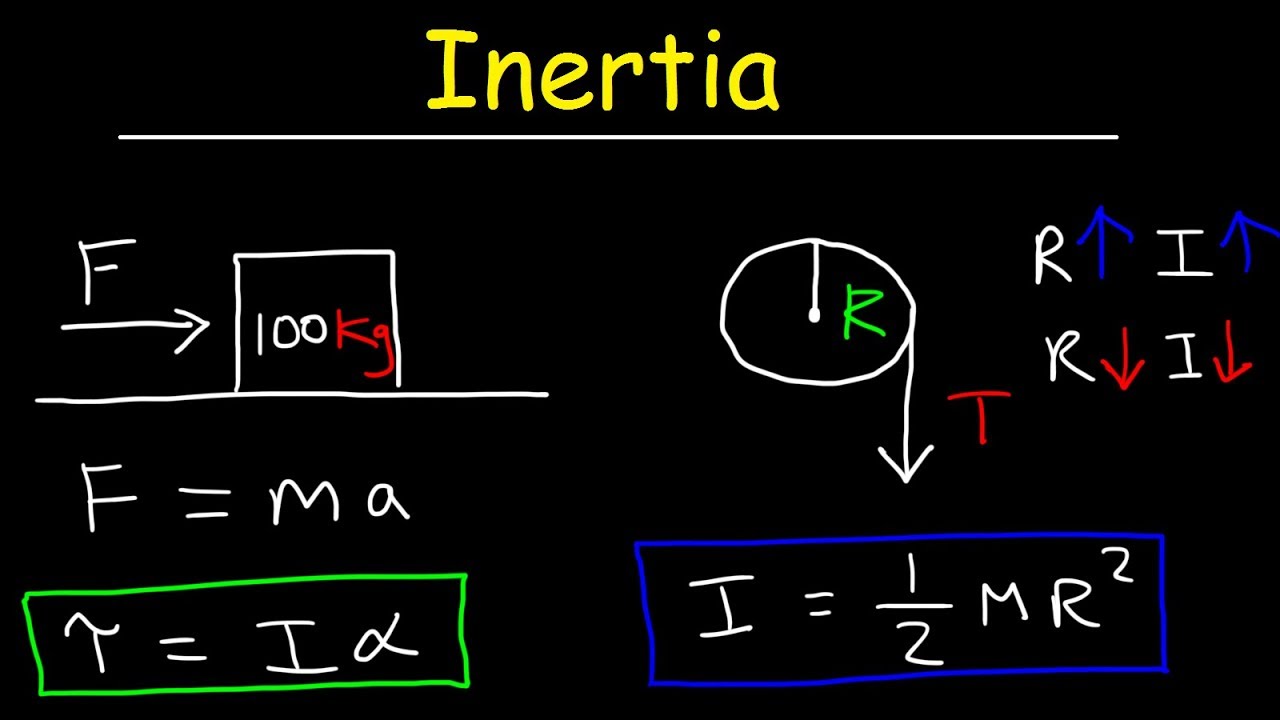
- 🔢 For a solid disk, the moment of inertia (I) is calculated as one-half the mass times the radius squared (1/2 M R^2), which is crucial for determining the object's speed after falling a certain height.
- ⚖️ The force of friction acts at the contact point and is responsible for the object's spin, but it does not do work if there's no slipping, thus no energy is lost to friction.
- 📋 When drawing forces acting on an object, it's important to note that the normal force and friction both act at the contact point, not from the center of mass.
- 🏗️ The speed of different rolling objects at the bottom of an incline depends on their individual moments of inertia; for example, a block will move faster than a disk of the same mass because it doesn't need to expend energy on rotational kinetic energy.
Q & A
What is the concept of 'rolling without slipping' in physics?
-Rolling without slipping is a special case in physics where an object rolls such that there is no relative motion between the object and the surface it is rolling on. This means there is no work done by friction, and thus, the mechanical energy is conserved.
How does the translational velocity and rotational velocity relate when an object is rolling without slipping?
-When an object is rolling without slipping, every point on the object has the same tangential velocity. The velocity of the center of mass is the same as the velocity of any point on the circle, and this combined motion results in the object's overall motion.
Why is there no work done by friction at the contact point when an object rolls without slipping?
-At the contact point, the instantaneous velocity of the object is zero because there is no slipping. Since work is defined as the force applied over a distance (W = F × d), and the distance (d) is zero when there is no slipping, no work is done by the frictional force.
How does the conservation of energy principle apply to an object rolling down an incline without slipping?
-The initial gravitational potential energy (MGH) of the object is converted into kinetic energy, which is split into linear kinetic energy (1/2 MV^2) and rotational kinetic energy (1/2 IΩ^2). Since there is no slipping, the total mechanical energy is conserved.
What is the relationship between linear speed and rotational speed for an object rolling without slipping?
-The linear speed (V) at the edge of the object is related to the rotational speed (Ω) by the equation V = RΩ, where R is the radius of the object. This relationship is key to understanding the combined motion of translation and rotation.
Why would an object with only translational motion (like a block sliding) move faster than an object that is also rotating when falling from the same height?
-An object with only translational motion does not need to use any of its gravitational potential energy for rotation. Therefore, all the potential energy (MGH) is converted into linear speed, making it move faster than an object that is also rotating, which has to use some of the energy for rotational kinetic energy.
What is the significance of the moment of inertia (I) in the context of an object rolling down an incline without slipping?
-The moment of inertia (I) determines the amount of rotational kinetic energy an object has. For a solid disk, I = 1/2 MR^2, and this value is used to calculate the rotational kinetic energy. Different objects with different moments of inertia will have different rotational speeds when rolling down an incline without slipping.
How does the force of friction contribute to the rotation of an object rolling without slipping?
-The force of friction acts to keep the object spinning as it rolls. However, since there is no slipping, this force does not do any work on the object, and thus, the mechanical energy of the system is conserved.
What is the difference between the forces acting on an object rolling down an incline and those acting on a freely falling object?
-In the case of an object rolling down an incline without slipping, there is an additional force of friction acting at the contact point, which contributes to the object's rotation. In contrast, a freely falling object is only subject to the force of gravity and does not experience this frictional force.
Why is it important to understand the direction and point of application of forces when analyzing an object rolling down an incline?
-Understanding the direction and point of application of forces is crucial for accurately analyzing the motion and energy transfer of the object. Forces such as the normal force and friction act at the contact point, not at the center of mass, and their correct representation affects the outcome of the problem.
How does the shape of an object affect its speed when rolling down an incline without slipping?
-The shape of an object affects its moment of inertia, which in turn influences the rotational kinetic energy. Objects with different shapes (e.g., a solid disk, a hoop, or a sphere) have different moments of inertia and thus will have different speeds when rolling down an incline without slipping from the same height.
Outlines
🎓 Understanding Rolling Without Slipping in Physics
The first paragraph introduces the concept of rolling without slipping, a fundamental topic in physics related to rotation. It explains that when an object rolls without slipping, it has both translational and rotational velocity, and there is no frictional work done, leading to the conservation of energy. The paragraph uses the example of an object rolling down an incline and spinning as it falls to illustrate the principles involved. It emphasizes that at the point of contact, the velocity is zero, which is a counterintuitive but crucial aspect of the no-slipping condition. The importance of this condition in conserving mechanical energy is highlighted.
📐 Conservation of Energy in a Falling Object with Rotation
The second paragraph delves into a specific example involving a string attached to a pulley, similar to a yo-yo, to demonstrate the conservation of energy. It outlines a scenario where the object falls a certain distance, and the tension in the string applies a constant torque without slipping. The paragraph explains the process of calculating the linear speed of the object after falling by using the conservation of energy principle, splitting the initial gravitational potential energy into linear and rotational kinetic energy components. It concludes with a comparison to freefall, noting that the object will move slower if it is spinning due to the energy required for rotation.
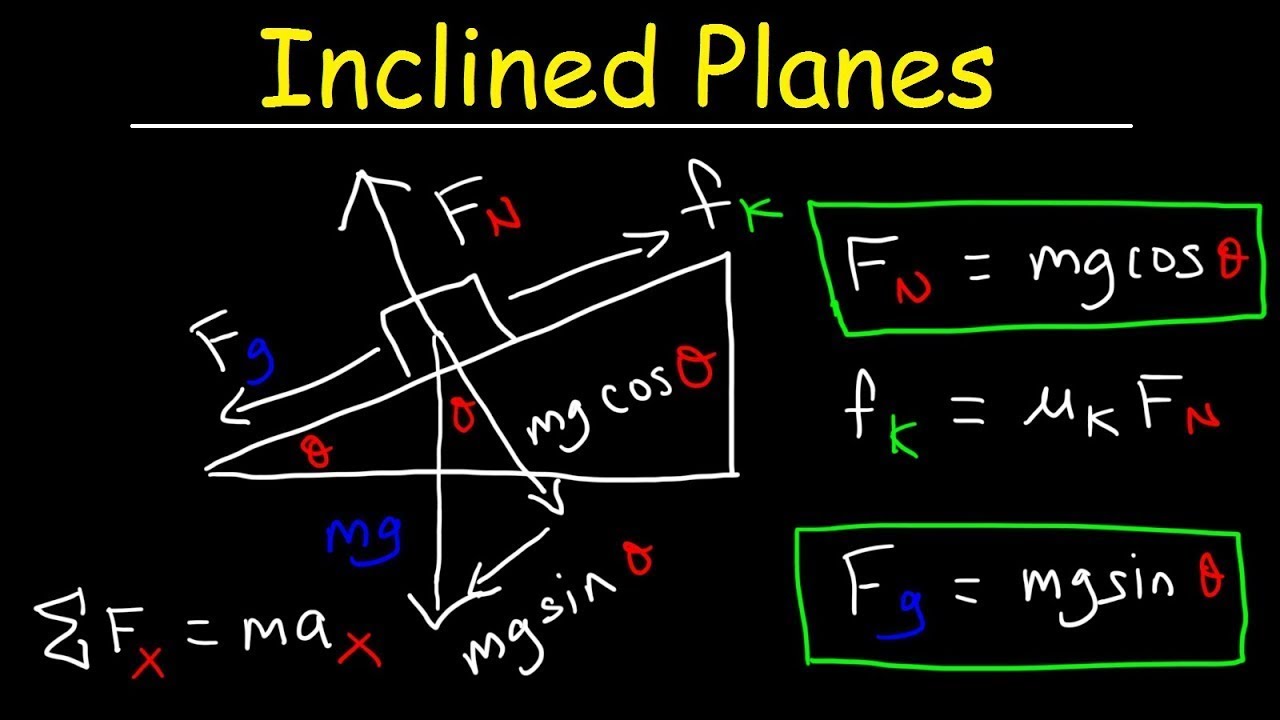
🧮 Analyzing Forces and Energy on an Inclined Plane
The third paragraph continues the discussion on energy conservation but introduces an inclined plane into the scenario. It emphasizes the importance of understanding the forces acting on an object, particularly the normal force and friction, which act at the contact point. The paragraph clarifies common mistakes made when students draw these forces and stresses the correct origin points of these forces. It then proceeds to solve for the speed of the object's center of mass at the bottom of the incline using energy conservation, noting that the presence of friction does not affect the work done as there is no displacement at the contact point. The paragraph concludes by discussing the impact of an object's moment of inertia on its speed at the bottom of the incline and comparing it to a block sliding down with negligible friction.
Mindmap
Keywords
💡Rolling without slipping
💡Translational velocity
💡Rotational velocity
💡Conservation of energy
💡Friction
💡Center of mass
💡Tangential velocity
💡Incline
💡Torque
💡Moment of inertia (I)
💡Free fall
Highlights
The concept of 'rolling without slipping' is a special case in physics where there is no work done by friction, leading to energy conservation.
Objects that roll without slipping have both translational and rotational velocity, and the velocity at the contact point is zero.
The tangential velocity of points on a rolling object is equal, and the object's velocity is centered around its center of mass.
When an object rolls, the particles on the top move translationally and also with some rotation, resulting in a combined velocity.
The force of friction in rolling without slipping acts to keep the object spinning but does not change displacement, thus no energy is lost due to friction.
Conservation of mechanical energy is key in rolling without slipping scenarios as there is no energy loss due to friction.
An example given is a string attached to a round object (like a yo-yo) which unwinds as it falls, maintaining no slipping between the string and the object.
The linear speed of an object after falling a certain distance can be calculated using conservation of energy principles.
The potential energy of an object is converted into linear and rotational kinetic energy, with the latter dependent on the object's moment of inertia.
Different objects (sphere, hoop, disc) rolling down an incline without slipping will have different speeds due to their varying moments of inertia.
A block sliding down an incline with negligible friction will move faster than a rolling object as it does not need to expend energy on rotational kinetic energy.
The force of normal originates at the contact point with the surface, not from the center of mass, which is a common mistake in force diagramming.
When solving for the speed of an object at the bottom of an incline, friction is not considered as it does no work in a no-slipping scenario.
The speed of the center of mass at the bottom of an incline is identical to the speed in free fall, given no slipping occurs.
Understanding the impact of an object's moment of inertia on its speed when rolling without slipping is crucial for AP Physics.
A qualitative question might ask whether a block in freefall or a rolling object without slipping would move faster, with the block being faster due to no rotational energy expenditure.
The lecture emphasizes the importance of understanding the nuances of rolling motion, energy conservation, and the role of friction in physics problems.
Transcripts
Browse More Related Video

Rotational Motion: Crash Course Physics #11
Inertia - Basic Introduction, Torque, Angular Acceleration, Newton's Second Law, Rotational Motion

AP Physics Lecture on Moment of Inertia. Watch this before 7.E

Rotational Equilibrium Introduction (and Static Equilibrium too!!)

8.01x - Lect 24 - Rolling Motion, Gyroscopes, VERY NON-INTUITIVE
Introduction to Inclined Planes
5.0 / 5 (0 votes)
Thanks for rating: