Second Derivative Test

The Organic Chemistry Tutor
4 Mar 201812:47
EducationalLearning
32 Likes 10 Comments

TLDRThis video script offers a comprehensive guide on utilizing the second derivative test to identify relative extrema in a function. It explains the process of finding critical numbers by setting the first derivative equal to zero and then using the second derivative to determine concavity. The script walks through two example functions, demonstrating how to calculate first and second derivatives, set up sign charts, and confirm extrema with both the second derivative test and the first derivative test. The clear explanation and step-by-step process make it an informative resource for understanding this mathematical concept.

Takeaways
  • 📈 The second derivative test is used to determine the presence of relative extrema in a function.
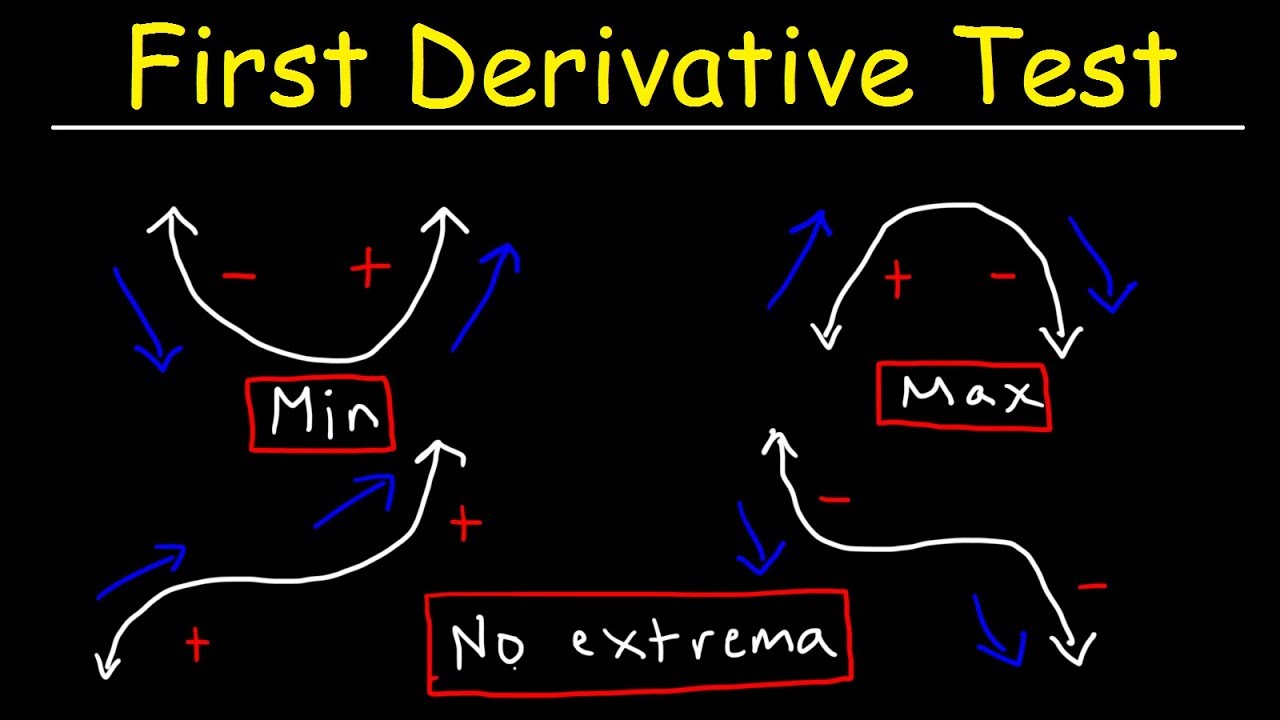
  • 🔍 To find a local maximum, the first derivative must equal zero at a critical point.
  • 🔧 For a local maximum, the second derivative at the critical point should be negative or less than zero, indicating a concave down shape.
  • 🔍 To find a local minimum, the first derivative must also equal zero at a critical point.
  • 🔧 For a local minimum, the second derivative at the critical point should be positive, indicating a concave up shape.
  • 📚 Example function: f(x) = 2x^3 - 12x^2. Find critical points by setting the first derivative equal to zero and factoring.
  • 📈 The second derivative test confirms a maximum at x=0 and a minimum at x=4 for the given example function.
  • 🔄 Use a sign chart to evaluate the second derivative for intervals around critical points to determine concavity.
  • 🔄 The first derivative test can be used to confirm the results of the second derivative test by examining the sign changes.
  • 📈 Another example function: f(x) = 4x^3 - 6x^2 - 24x + 1. Identify critical points at x=-1 and x=2.
  • 🔧 Applying the second derivative test to the second example function confirms a maximum at x=-1 and a minimum at x=2.
Q & A

  • What is the purpose of the second derivative test in the context of the given video?

    -The purpose of the second derivative test is to determine if there are any relative extrema, such as local maxima or minima, in a function.

  • What is a critical number in the context of finding local maxima or minima?

    -A critical number is a value of the independent variable (x) at which the first derivative of the function equals zero. This is the point where a local maximum or minimum can occur on the x-axis.

  • What is the condition for a critical point to be a local maximum according to the second derivative test?

    -For a critical point to be a local maximum, the second derivative at that point must be negative or less than zero, indicating that the function is concave down at that point.

  • How does the second derivative test help in identifying a local minimum in a function?

    -The second derivative test helps in identifying a local minimum by checking if the second derivative at a critical point is positive or greater than zero, indicating the function is concave up at that point.

  • What is the first step in applying the second derivative test to a function?

    -The first step in applying the second derivative test is to find the first derivative of the function and then set it equal to zero to identify the critical numbers.

  • What is the relationship between the first and second derivatives in determining the concavity of a function?

    -The first derivative can help identify critical numbers where the function might have extrema. The second derivative, when evaluated at these critical numbers, can then determine the concavity (concave up for minima, concave down for maxima) and thus confirm the nature of the extrema.

  • How does the sign of the second derivative relate to the concavity of a graph?

    -A positive second derivative indicates that the graph is concave up, while a negative second derivative indicates that the graph is concave down.

  • What is the first derivative of the function f(x) = 2x^3 - 12x^2?

    -The first derivative of the function f(x) = 2x^3 - 12x^2 is f'(x) = 6x^2 - 24x.

  • What are the critical numbers for the function f(x) = 2x^3 - 12x^2?

    -The critical numbers for the function f(x) = 2x^3 - 12x^2 are x = 0 and x = 4, found by setting the first derivative equal to zero and solving for x.

  • How can the first derivative test confirm the results of the second derivative test?

    -The first derivative test can confirm the results of the second derivative test by using the sign of the first derivative around the critical numbers to determine whether the function is increasing or decreasing, which in turn indicates a maximum or minimum at those points.

  • What is the second derivative of the function f(x) = 4x^3 - 6x^2 - 24x + 1?

    -The second derivative of the function f(x) = 4x^3 - 6x^2 - 24x + 1 is f''(x) = 24x - 12 - 12, which simplifies to f''(x) = 24x - 24.

  • What are the critical numbers for the function f(x) = 4x^3 - 6x^2 - 24x + 1?

    -The critical numbers for the function f(x) = 4x^3 - 6x^2 - 24x + 1 are x = -1 and x = 2, found by setting the first derivative equal to zero and solving for x.

Outlines
00:00
📚 Introduction to the Second Derivative Test

This paragraph introduces the concept of the second derivative test, a method used to identify relative extrema in a function. It explains that to find a local maximum or minimum, one must first determine the critical numbers where the first derivative equals zero. The paragraph then describes how the second derivative indicates the concavity of the function at these critical points, with a negative second derivative suggesting a local maximum (concave down) and a positive second derivative indicating a local minimum (concave up). An example function is provided to illustrate the process.

05:01
🧐 Applying the Second Derivative Test

In this paragraph, the script walks through the application of the second derivative test on a given function. It demonstrates how to calculate the first and second derivatives and use them to identify critical numbers and determine the nature of the extrema (maximum or minimum) at these points. The explanation includes the creation of a sign chart to understand the concavity and how to evaluate the second derivative at specific critical numbers. This process helps confirm whether the function has a local minimum or maximum at the critical points.

10:04
🔍 Confirming Results with the First Derivative Test

The final paragraph focuses on confirming the results obtained from the second derivative test using the first derivative test. It reiterates the process of identifying critical numbers and analyzing the function's behavior around these points using the first derivative. The paragraph emphasizes the importance of understanding the function's increasing and decreasing intervals to confirm the presence of a maximum or minimum. The explanation concludes with a summary of how the second derivative test can be used to determine relative extrema and how the first derivative test can be used to confirm these findings.

Mindmap
Keywords
💡Second Derivative Test
The Second Derivative Test is a method used in calculus to determine the nature of a critical point - whether it is a local maximum, local minimum, or neither. In the video, it is explained that if the second derivative at a critical point is negative, the function has a local maximum at that point, and if the second derivative is positive, the function has a local minimum. This concept is central to the video's theme of identifying relative extrema in a function.
💡Relative Extrema
Relative extrema refer to the local maximum or minimum values of a function within a certain interval. In the context of the video, relative extrema are the points where the graph of the function changes from increasing to decreasing (local maximum) or from decreasing to increasing (local minimum). The video focuses on using the second derivative test to identify these points within a function.
💡Critical Numbers
Critical numbers are the values of the independent variable (usually x) at which the first derivative of a function is either zero or undefined. These points are potential locations for the function to have a local maximum, local minimum, or neither. In the video, finding critical numbers is the first step in using the second derivative test to identify relative extrema.
💡First Derivative
The first derivative of a function represents the slope of the tangent line to the graph of the function at any given point. It is used to determine the rate of change of a function and to identify critical numbers where the function may have a local maximum or minimum. In the video, calculating the first derivative is essential to find the points where the function could potentially have relative extrema.
💡Concavity
Concavity refers to the curvature of a graph of a function. A function is said to be concave up when the graph curves in a way that the curve lies above its tangent line, and concave down when it curves below its tangent line. In the video, the concavity of a function at a critical number, as determined by the sign of the second derivative, is crucial in identifying whether the point is a local maximum or minimum.
💡First Derivative Test
The First Derivative Test is another method used to confirm the nature of critical points found in a function. It involves examining the sign changes of the first derivative on either side of a critical number to determine if there is a local maximum, local minimum, or neither. In the video, the First Derivative Test is used to confirm the results obtained from the Second Derivative Test.
💡Factoring
Factoring is the process of breaking down a polynomial into its factors, which are simpler expressions that when multiplied together, give the original polynomial. In the context of the video, factoring is used to simplify the first and second derivatives of the given functions, making it easier to set them equal to zero and find the critical numbers.
💡Graph
In mathematics, a graph is a visual representation of the relationship between variables, in this case, the function and its derivatives. The graph of a function helps visualize its behavior, including extrema, concavity, and critical points. The video uses the concept of a graph to illustrate how the First and Second Derivative Tests relate to the shape and features of a function's graph.
💡Sign Chart
A sign chart is a tool used in calculus to determine the intervals where a function is increasing or decreasing based on the sign of its derivative. In the video, a sign chart is used to visually represent how the sign of the first derivative changes around the critical numbers, further confirming the nature of the extrema.
💡Derivative
A derivative in calculus is a measure of how a function changes as its input changes. It is the foundation for analyzing the behavior of functions, including finding rates of change, critical points, and extrema. The video focuses on using both the first and second derivatives to analyze and determine the nature of extrema in a function.
💡Local Maximum/Minimum
A local maximum or minimum is a point on the graph of a function where the function reaches a highest or lowest value in its immediate vicinity. These are temporary peaks or valleys before the function continues to increase or decrease. The video's main theme is to teach how to find and confirm the locations of local maxima and minima using the first and second derivatives of a function.
Highlights

Introduction to the second derivative test for determining relative extrema in a function.

A local maximum requires the first derivative to equal zero at a critical point.

The second derivative at a critical point must be negative for a local maximum.

For a local minimum, the second derivative at the critical point must be positive.

Example function given as f(x) = 2x^3 - 12x^2 to apply the second derivative test.

Derivative calculation for the given example function.

Determination of critical numbers by setting the first derivative equal to zero.

Factoring out the greatest common factor to find critical numbers.

Second derivative calculation for the given example function.

Identification of an inflection point at x=2 through second derivative analysis.

Use of a sign chart to determine concavity and extrema.

Confirmation of relative extrema using the first derivative test.

Second example function provided as f(x) = 4x^3 - 6x^2 - 24x + 1.

Critical numbers found for the second example function using the first derivative.

Second derivative analysis for the second example function's critical numbers.

Confirmation of extrema for the second example function using the first derivative test.

Summary of how to use the second derivative test to find relative extrema.

Emphasis on the importance of identifying critical numbers and the sign of the second derivative.

Conclusion of the video, highlighting the process and the practical application of the second derivative test.

Transcripts

Browse More Related Video

Calculus AB Homework 4.4: Relative Extrema

First Derivative Test

3.2 - Using Second Derivatives to Classify Max and Min Values

Second Derivative Test

Use the Second Derivative Test to Find Any Extrema and Saddle Points: f(x,y) = -4x^2 + 8y^2 - 3

Second Derivative Test Multivariable (Calculus 3)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsCalculusDerivative TestExtremaCritical NumbersLocal MaximumLocal MinimumFirst DerivativeSecond DerivativeFactoringSign Chart