Marginal Cost, Marginal Revenue, and Marginal Profit

The Organic Chemistry Tutor
6 Mar 201818:56
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses cost, demand, and profit functions in the context of a company's production decisions. It explains how to calculate the average selling price, revenue, total cost, and profit at a specific production level. The script then demonstrates how to find the production level that maximizes profit by setting the first derivative of the profit function to zero. It also introduces the concepts of marginal profit, marginal revenue, and marginal cost, and their roles in determining the optimal production level for maximizing profit. The video concludes with a practical example of calculating the maximum profit and the associated production level.

Takeaways
  • 📉 The average selling price at a production level of 500 units is $45 per unit, calculated by taking the given price function ($50 - $0.01 * quantity) and plugging in 500 units.
  • 💰 The total revenue at a production level of 500 units is $22,500, which is found by multiplying the production level (500 units) by the average price per unit ($45).
  • 📈 The total cost at a production level of 500 units is $7,000, as provided by the total cost function.
  • 🚀 The profit at a production level of 500 units is $15,500, which is calculated by subtracting the total cost ($7,000) from the total revenue ($22,500).
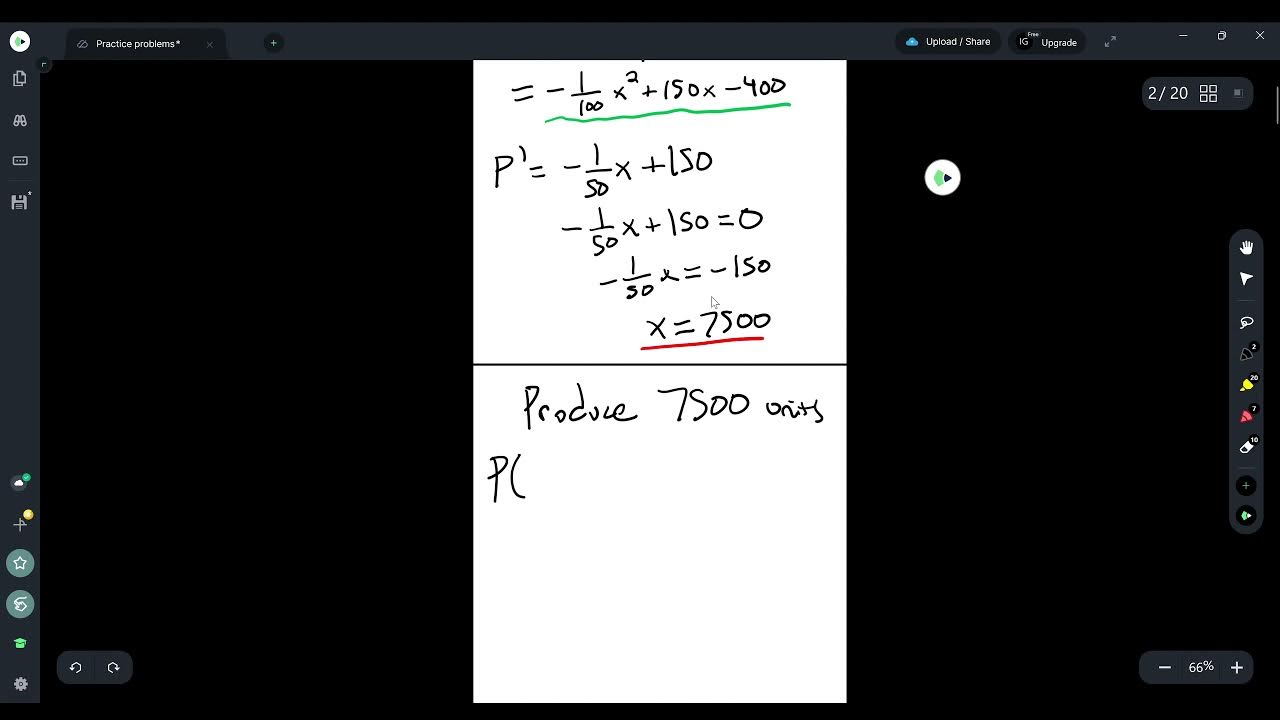
  • 🔍 To find the production level that maximizes profit, we set the first derivative of the profit function (marginal profit) equal to zero and solve for the production level (x).
  • 🏆 The production level that maximizes profit is 1,150 units, as determined by setting the marginal revenue equal to the marginal cost and solving for x.
  • 🌟 The maximum profit the company can achieve is $23,950 by selling 1,150 units, calculated using the profit function at the optimal production level.
  • 📊 The marginal profit at a production level of 500 units is $26 per unit, indicating the approximate change in profit if an additional unit is sold.
  • 🔄 The marginal profit, marginal revenue, and marginal cost are all important concepts for understanding how changes in production levels affect a company's financial outcomes.
  • 📝 The profit, revenue, and cost functions are essential tools for businesses to make informed decisions about production levels and pricing strategies.
Q & A

  • What is the average selling price at a production level of 500 units?

    -The average selling price at a production level of 500 units is $45 per unit.

  • How is the revenue calculated for 500 units?

    -The revenue for 500 units is calculated by multiplying the production level (500) by the selling price ($45), which results in a total revenue of $22,500.

  • What is the total cost at a production level of 500 units?

    -The total cost at a production level of 500 units is $7,000.

  • What is the profit at a production level of 500 units?

    -The profit at a production level of 500 units is $15,500, which is the difference between the revenue ($22,500) and the total cost ($7,000).

  • How can you find the production level that maximizes profit?

    -To find the production level that maximizes profit, you set the first derivative of the profit function (marginal profit) equal to zero and solve for x. Alternatively, you set the marginal revenue equal to the marginal cost.

  • What production level results in the maximum profit?

    -A production level of 1,150 units results in the maximum profit.

  • What is the maximum profit the company can make?

    -The maximum profit the company can make is $23,950 by selling 1,150 units.

  • What does the marginal profit at a production level of 500 units indicate?

    -The marginal profit at a production level of 500 units is $26 per unit, which represents the approximate increase in profit when selling one additional unit.

  • How do you calculate the marginal profit at a production level of 500 units?

    -The marginal profit at a production level of 500 units is calculated by evaluating the derivative of the profit function at x=500, which is 46 - 0.04(500), resulting in $26.

  • What do marginal revenue and marginal cost represent?

    -Marginal revenue represents the change in revenue when selling one more unit, and marginal cost represents the change in total cost when producing and selling one additional unit.

  • How can you verify that the calculated production level indeed results in the maximum profit?

    -You can verify this by calculating the profit at various production levels around the calculated maximum (1,150 units), such as 1,000, 1,300, and 1,500 units, and comparing the profits to ensure that the calculated maximum is indeed the highest value.

Outlines
00:00
📈 Price Function and Revenue Calculation

This paragraph explains the concept of the price function, which is also known as the demand function, and how it differs from the profit function. It provides a specific example where the average selling price is calculated for 500 units of production. The paragraph then moves on to explain the revenue function, showing how to calculate total revenue at a production level of 500 units. The explanation includes a breakdown of the revenue equation and a clear demonstration of how the total revenue of $22,500 is derived from selling 500 units at $45 per unit.

05:07
💰 Total Cost, Profit Calculation, and Profit Maximization

The second paragraph delves into the total cost and profit of the company at a production level of 500 units. It begins by calculating the total cost and then moves on to determine the profit by subtracting the cost from the revenue. The paragraph also introduces the concept of profit maximization, explaining how to find the production level that yields the maximum profit. This is done by setting the first derivative of the profit function (marginal profit) equal to zero, which results in the optimal production level of 1150 units. The paragraph concludes with a calculation of the maximum profit, which is $23,950, and verifies this by comparing profits at different production levels.

10:08
📊 Marginal Profit Calculation and Analysis

This paragraph focuses on the calculation and interpretation of marginal profit. It defines marginal profit as the change in profit for selling an additional unit and provides the formula for calculating it. The paragraph calculates the marginal profit at a production level of 500 units and explains its significance. It also compares the marginal profit at 500 units with the profit change when producing one more unit. Furthermore, the paragraph explains the concepts of marginal revenue and marginal cost, highlighting their importance in understanding the financial impact of changes in production levels.

Mindmap
Keywords
💡Cost and Demand Functions
The cost and demand functions are mathematical equations that represent the relationship between the cost of production and the quantity produced, as well as the relationship between the selling price and the quantity demanded by consumers. In the video, these functions are essential for determining the average selling price at a specific production level, which is a critical factor in understanding profitability. The script uses these functions to calculate the price at a production level of 500 units, highlighting the importance of these functions in business decision-making.
💡Average Selling Price
The average selling price refers to the price at which a company sells its goods or services over a certain period, taking into account the total quantity sold. In the context of the video, the average selling price is calculated using the demand function, which is a key component in determining the revenue and profit for the company. Understanding the average selling price is crucial for businesses as it helps in setting pricing strategies and estimating revenue.
💡Revenue Function
The revenue function, also known as the sales function, represents the total income generated from selling a product or service. It is calculated by multiplying the production level (quantity sold) by the selling price per unit. In the video, the revenue function is used to determine the total revenue at a production level of 500 units, which is an essential metric for assessing a company's financial performance.
💡Total Cost
Total cost refers to the sum of all expenses incurred by a company in the production process, including fixed costs (which do not change with the level of production) and variable costs (which change with the level of production). Understanding the total cost is vital for businesses as it helps in determining profitability and making decisions about production levels. In the video, the total cost is calculated using a given function, which is then used to find the profit at different production levels.
💡Profit Function
The profit function represents the difference between the total revenue a company generates and the total costs it incurs. It is a key indicator of a company's financial health and profitability. In the video, the profit function is derived from the revenue and cost functions and is used to calculate the profit at various production levels, as well as to determine the optimal production level that maximizes profit.
💡Marginal Profit
Marginal profit refers to the additional profit generated from selling one more unit of a product. It is the first derivative of the profit function and indicates the change in profit with respect to changes in the number of units sold. Understanding marginal profit is important for businesses as it helps in making decisions about production levels and pricing strategies to maximize overall profit.
💡Maximum Profit
Maximum profit is the highest level of profit that a company can achieve at a particular production level. It is the point at which the profit function reaches its peak value. Businesses aim to identify this production level to optimize their financial performance. In the video, the maximum profit is determined by setting the first derivative of the profit function (marginal profit) equal to zero and solving for the production level.
💡Marginal Revenue
Marginal revenue is the additional revenue generated from selling one more unit of a product. It is the first derivative of the revenue function and represents the change in revenue with respect to changes in the number of units sold. Understanding marginal revenue helps businesses to assess the impact of selling additional units on their total revenue and to make informed decisions about production and pricing.
💡Marginal Cost
Marginal cost is the additional cost incurred from producing one more unit of a product. It is the first derivative of the cost function and represents the change in total cost with respect to changes in the production level. Knowing the marginal cost is crucial for businesses as it aids in determining the most cost-effective production levels and pricing strategies.
💡First Derivative
The first derivative of a function represents the rate of change or the slope of the function at any given point. In the context of the video, the first derivative is used to find the marginal profit, marginal revenue, and marginal cost, which are essential for determining the optimal production level and maximizing profit. The first derivative is set to zero to find the maximum or minimum values of a function.
💡Optimal Production Level
The optimal production level is the quantity of goods or services that a company should produce to achieve the best possible financial outcome, such as maximizing profit or minimizing cost. It is determined by analyzing the cost, revenue, and profit functions, and is often found by setting the first derivative of the profit function to zero. In the video, the optimal production level is identified as the point where the company can make the most profit.
Highlights

The average selling price at a production level of 500 units is $45 per unit.

The revenue function is defined as the production level times the selling price, represented as x times (50 - 0.01x).

At a production level of 500 units, the total revenue is $22,500.

The total cost at a production level of 500 units is $7,000.

The profit function is the difference between the revenue function and the cost function.

The profit at a production level of 500 units is $15,500.

To maximize profit, the production level should be set where the marginal profit is equal to zero.

The production level that maximizes profit is 1150 units.

The maximum profit the company can make is $23,950 by selling 1150 units.

The marginal profit at a production level of 500 units is $26 per unit.

Marginal profit represents the change in profit if an additional unit is sold.

Marginal revenue and marginal cost help in understanding the change in revenue and cost for selling an additional unit.

The maximum profit is confirmed by comparing profits at different production levels around the maximum point.

The profit decreases as production levels move away from the optimal level of 1150 units.

The concepts of marginal profit, revenue, and cost are crucial for business decision-making.

The video provides a comprehensive understanding of cost, demand, revenue, and profit functions in a business context.

Transcripts

Browse More Related Video

Marginal Revenue, Average Cost, Profit, Price & Demand Function - Calculus

Math 1325 Lecture 12 4

Math 1325 Lecture 9 9 - Applications

BusCalc 10 Marginal Profit

Optimization Problem Examples

Marginal cost & differential calculus | Applications of derivatives | AP Calculus AB | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Economic AnalysisProfit MaximizationCost-Demand-ProfitBusiness StrategyProduction OptimizationMarginal AnalysisMathematical ModelingFinancial PlanningEconomic ConceptsBusiness Education