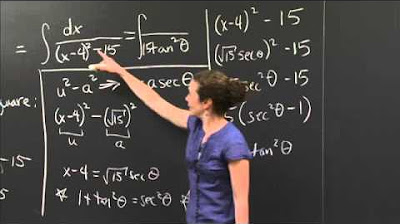Integrals: Trig Substitution 1

Khan Academy

14 Oct 200907:38

EducationalLearning

32 Likes 10 Comments

TLDRThe video script presents a method for finding the indefinite integral of a function involving a square root and an x term. The approach involves recognizing a trigonometric identity within the function, performing algebraic manipulations, and substituting with trigonometric functions. The process includes solving for x and theta, finding the derivative dx/dtheta, and substituting these into the integral. The result is simplified to an integral in terms of theta, which is then evaluated and expressed back in terms of x, completing the antiderivative process.

Takeaways

🌟 The problem involves finding the indefinite integral of a function that does not lend itself to traditional integration methods.
🔍 The approach taken is to recognize a similarity between the given function and a trigonometric identity, specifically the Pythagorean identity for sine and cosine.
📐 The script suggests factoring out a 3 from the denominator to make the given expression resemble the trigonometric identity more closely.
🌐 A substitution is made where 2/3x^2 is equated to sine squared theta, allowing the use of the trigonometric identity to simplify the integral.
🔄 The process involves solving for both x and theta in terms of the trigonometric substitution.
📚 The derivative of x with respect to theta is found, which is crucial for the substitution process in the integral.
📈 The integral is then rewritten with the trigonometric expressions, and the terms are simplified and canceled out.
🎓 The antiderivative is initially found in terms of theta, which is then substituted back with the original x variable to find the final result.
🎉 The final result of the indefinite integral is expressed as 1 over the square root of 2 times the arcsine of (square root of 2 over square root of 3x) plus an arbitrary constant.
📝 The method demonstrated is a creative application of trigonometric identities and substitution to solve a non-standard integral problem.

Q & A

What is the integral expression given in the script?
-The integral expression is 1 over the square root of 3 minus 2x squared with respect to x (dx).
Why is the traditional u-substitution method not applicable here?
-The traditional u-substitution method is not directly applicable because there is no obvious derivative of the integrand that can be easily isolated and replaced with u.
What trigonometric identity does the script suggest using for integration?
-The script suggests using the trigonometric identity sine squared theta plus cosine squared theta equals 1, and then rearranges it to cosine squared theta equals 1 minus sine squared theta for comparison with the integrand.
How does the script relate the given integral to a trigonometric function?
-By factoring out a 3 from the denominator and setting 2/3x squared equal to sine squared theta, the integral is related to a trigonometric function, allowing the use of trigonometric identities for integration.
What substitution is made to transform the integral?
-The substitution made is setting 2/3x squared equal to sine squared theta, and then taking the square root of both sides of the equation to relate x and theta.
How is dx with respect to d theta derived in the process?
-The derivative of x with respect to theta is found by taking the derivative of the equation relating x and theta, resulting in dx being equal to the square root of 3 over the square root of 2 cosine of theta d theta.
What is the simplified form of the integral after substitution and simplification?
-The simplified form of the integral is 1 over the square root of 2 d theta, which represents the antiderivative with respect to theta.
How is the constant of integration (c) represented in the final answer?
-The constant of integration is represented as an arbitrary constant plus the integral of 1 over the square root of 2 times d theta.
What is the final form of the antiderivative in terms of x?
-The final form of the antiderivative in terms of x is 1 over the square root of 2 times the arcsine of square root of 2 over square root of 3 x, plus an arbitrary constant.
Why is the reverse substitution necessary in this process?
-Reverse substitution is necessary to express the antiderivative in terms of the original variable x, rather than the substitution variable theta.
What is the main strategy used in this script for solving the integral?
-The main strategy used in this script is recognizing the similarity between the integrand and trigonometric identities, and then performing a suitable substitution and simplification to find the antiderivative.

Outlines

00:00

📚 Trigonometric Substitution in Indefinite Integrals

The paragraph discusses the process of solving an indefinite integral using trigonometric substitution. The integral in question is 1 over the square root of 3 minus 2x squared dx. The speaker explains that traditional methods like u-substitution are not applicable here, and instead, a trigonometric identity is used. The identity used is the Pythagorean identity for sine and cosine, which is modified to resemble the given integral. The speaker then sets 2/3x squared equal to sine squared theta and proceeds to solve for x and theta, eventually expressing dx in terms of d theta. This allows for the substitution into the integral, which simplifies to 1 over the square root of 2 d theta. The speaker emphasizes the importance of reversing the substitution to express the antiderivative in terms of x, resulting in the final answer of 1 over the square root of 2 times the arcsine of square root of 2 over square root of 3 x, plus an arbitrary constant.

05:05

🔍 Simplification and Reverse Substitution in Trigonometric Integrals

The second paragraph continues from the previous one, focusing on the simplification of the indefinite integral obtained through trigonometric substitution. The speaker simplifies the integral by canceling out terms and taking the square root of the denominator, resulting in an expression involving cosine of theta. The integral is then further simplified to 1 over the square root of 2 times theta plus a constant. The speaker highlights the need to reverse substitute to express the antiderivative in terms of x, using the previously found relationship between x and theta. The final result is the antiderivative of the original function in terms of x, demonstrating the effectiveness of the trigonometric substitution method.

Mindmap

Keywords

💡Indefinite Integral

An indefinite integral represents a family of functions that differ by a constant, known as the constant of integration, which is denoted by 'c'. In the context of the video, the indefinite integral is the antiderivative of the given function, which is the mathematical operation of finding a function whose derivative is the function we're integrating. The video focuses on finding the indefinite integral of 1 over the square root of 3 minus 2x squared, which is a non-standard integral requiring a creative approach.

💡Trigonometric Identity

A trigonometric identity is an equation that holds true for all values of the variables involved, relating different trigonometric functions of the same angle. In the video, the identity sin^2(θ) + cos^2(θ) = 1 is used as a starting point for the substitution method. The identity is manipulated to resemble the integrand's form, which allows the substitution of trigonometric functions into the integral.

💡Substitution

Substitution is a technique used in calculus to simplify integrals by replacing the variable of integration with another variable or an expression involving the original variable. In the video, the substitution method is employed by setting 2/3x^2 equal to sin^2(θ), which transforms the integrand into a form that can be integrated using basic trigonometric identities. This method is crucial for solving non-standard integrals that do not have a straightforward antiderivative.

💡Factoring

Factoring is the process of breaking down a polynomial into a product of its factors, which are simpler expressions. In the video, factoring is used to isolate the constant 3 in the denominator, which simplifies the integrand and makes it easier to apply the trigonometric substitution. This step is essential for creating a form that resembles a known trigonometric identity.

💡Derivative

The derivative of a function is a measure of the rate at which the function changes with respect to its independent variable. In the context of the video, the derivative is used to find the relationship between x and θ, which is necessary for the reverse substitution after the integration with respect to θ. Understanding derivatives is crucial for the substitution method, as it helps to convert back to the original variable after the integration is complete.

💡Reverse Substitution

Reverse substitution is the process of replacing the substituted variable back into the solution to obtain the original variable's form. After performing the integration with respect to the substituted variable (θ in this case), the final step is to express the result in terms of the original variable (x). This is necessary to provide the solution in a form that is directly applicable to the original problem.

💡Arbitrary Constant

The arbitrary constant, denoted by 'c', is an additional term that is added to the antiderivative of a function to account for the infinite number of functions that can have the same derivative. In the context of the video, after finding the indefinite integral with respect to θ, an arbitrary constant 'c' is added to account for the family of functions that satisfy the original differential equation.

💡Trigonometric Functions

Trigonometric functions, such as sine and cosine, are mathematical functions that relate the angles and sides of a right triangle or periodic phenomena. In the video, these functions are used to perform a trigonometric substitution, which simplifies the integral of a function that resembles a trigonometric identity. The sine and cosine functions are key to transforming the integrand into a more manageable form.

💡Integration

Integration is the process of finding the antiderivative, or the reverse process of differentiation, of a given function. It is a fundamental operation in calculus that helps in solving problems involving accumulation of quantities and areas under curves. The video demonstrates the integration process for a non-standard integral using trigonometric substitution, which is a technique for integrating functions that do not have a simple antiderivative.

💡Algebraic Manipulation

Algebraic manipulation refers to the process of transforming and rearranging mathematical expressions using the rules of algebra. In the video, algebraic manipulation is used to change the form of the integrand to match a known trigonometric identity, which allows for the application of substitution. This technique is essential for solving complex integrals that do not have obvious antiderivatives.

💡Unit Circle

The unit circle is a circle with a radius of 1 centered at the origin of a coordinate system. It is a fundamental concept in trigonometry, as it provides a geometric interpretation of the sine and cosine functions for angles measured in radians. In the video, the unit circle is implicitly used as the basis for the trigonometric identity that is key to the substitution method.

Highlights

The indefinite integral of 1 over the square root of 3 minus 2x squared is discussed.

Traditional methods of taking this antiderivative are not immediately apparent.

A trigonometric identity from the unit circle definition is used for comparison.

The identity sine squared theta plus cosine squared theta equals 1 is utilized.

Algebraic manipulation is performed to make the integral expression resemble a trigonometric form.

The expression 3 times 1 minus 2/3x squared is factored out of the denominator.

A substitution is made setting 2/3x squared equal to sine squared theta.

The relationship between x and theta is derived through square root relationships.

The derivative of x with respect to theta is calculated as square root of 3 over square root of 2 cosine of theta.

The integral is rewritten with respect to d theta, replacing dx with its equivalent expression.

The integral simplifies to the form of 1 over the square root of 2 d theta.

The antiderivative is expressed as 1 over the square root of 2 times theta plus a constant.

The final step involves reversing the substitution to express the antiderivative in terms of x.

The antiderivative is found to be 1 over the square root of 2 times the arcsine of square root of 2 over square root of 3 x, plus a constant.

The video aims to familiarize viewers with solving complex integrals using trigonometric identities and substitution.

Transcripts

Browse More Related Video

Integrals: Trig Substitution 2

Integration by completing the square | MIT 18.01SC Single Variable Calculus, Fall 2010

Definite Integral With U-Substitution

Integrals: Trig Substitution 3 (long problem)

Back Substitution - When a u-sub doesn't match cleanly!

Optimisation Grade 12

Integrals: Trig Substitution 1

Takeaways

Q & A

What is the integral expression given in the script?

Why is the traditional u-substitution method not applicable here?

What trigonometric identity does the script suggest using for integration?

How does the script relate the given integral to a trigonometric function?

What substitution is made to transform the integral?

How is dx with respect to d theta derived in the process?

What is the simplified form of the integral after substitution and simplification?

How is the constant of integration (c) represented in the final answer?

What is the final form of the antiderivative in terms of x?

Why is the reverse substitution necessary in this process?

What is the main strategy used in this script for solving the integral?