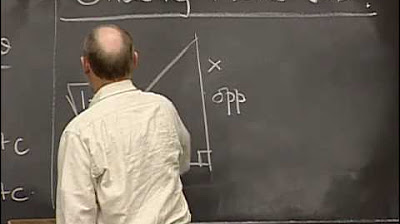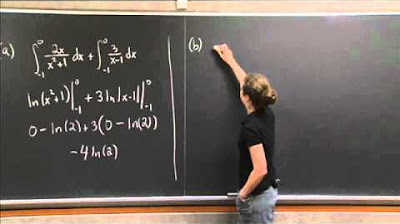Integration by completing the square | MIT 18.01SC Single Variable Calculus, Fall 2010

MIT OpenCourseWare

7 Jan 201114:04

EducationalLearning

32 Likes 10 Comments

TLDRIn this video, the instructor demonstrates how to find an antiderivative of the function 1/(x² - 8x + 1) using the technique of completing the square. After completing the square, the problem is transformed for a trigonometric substitution. The process involves detailed algebraic manipulation and the use of trigonometric identities to simplify the integral. The final steps include finding the antiderivative in terms of trigonometric functions and converting back to the original variable using a right triangle. This comprehensive example highlights a strategic approach to solving integrals involving quadratic expressions.

Takeaways

📚 The video is a math tutorial focusing on finding the antiderivative of a given function using a specific technique.
🔍 The function to integrate is \( \frac{1}{x^2 - 8x + 1} \), and the method used is completing the square to simplify the expression.
📐 The process involves transforming the quadratic expression into a perfect square to facilitate integration.
🔢 The step-by-step algebraic manipulation includes adding and subtracting 15 to complete the square, resulting in \( x - 4 \) squared.
📉 The technique of trigonometric substitution is introduced to further simplify the integral into a form involving secant and tangent functions.
📝 The substitution involves setting \( x - 4 = \sqrt{15} \sec(\theta) \), which allows rewriting the integral in terms of trigonometric identities.
📈 The identity \( 1 + \tan^2(\theta) = \sec^2(\theta) \) is used to simplify the denominator of the integral.
📌 The derivative of secant, which involves tangent, is used to express \( dx \) in terms of \( d\theta \), connecting the integral back to the original variable x.
📚 The integral is then simplified to involve \( \csc(\theta) \), which is the antiderivative needed to solve the problem.
📝 The final step involves substituting back to the original variable x using a triangle representation and the relationships between x, theta, and the sides of the triangle.
📈 The video concludes with a summary of the steps taken and a visual representation of the triangle used for the final substitution.

Q & A

What is the main objective of the video script?
-The main objective is to find the antiderivative of the function \( \frac{1}{x^2 - 8x + 1} \) using the technique of completing the square and trigonometric substitution.
Why is the technique of completing the square used in this video?
-Completing the square is used because the function cannot be easily integrated using partial fractions, and it sets up the function for a trigonometric substitution.
What is the first step in the process of completing the square for the given function?
-The first step is to rewrite the quadratic expression in the denominator to form a perfect square, which involves identifying the correct term to complete the square and adjusting the constant term accordingly.
How does the video script suggest checking the correctness of the antiderivative found?
-The correctness of the antiderivative can be checked by differentiating the antiderivative and verifying if it results in the original function \( \frac{1}{x^2 - 8x + 1} \).
What trigonometric identity is used in the script to simplify the denominator after the trigonometric substitution?
-The trigonometric identity used is \( 1 + \tan^2(\theta) = \sec^2(\theta) \), which helps to express the denominator in terms of \( \tan^2(\theta) \).
What is the role of the substitution \( x - 4 = \sqrt{15} \sec(\theta) \) in the process?
-This substitution is used to transform the integral into a form that can be solved using trigonometric functions, specifically by expressing the denominator in terms of \( \tan^2(\theta) \) and finding \( dx \) in terms of \( d\theta \).
How does the script simplify the expression \( \sqrt{15} \sec(\theta) \tan(\theta) \) in the integral?
-The expression is simplified by dividing out common factors and recognizing that \( \sec(\theta) = \frac{1}{\cos(\theta)} \) and \( \tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)} \), which leads to the integral of \( \csc(\theta) \).
What is the final step in finding the antiderivative according to the script?
-The final step is to find the antiderivative of \( \csc(\theta) \) and then substitute back for \( \theta \) using the triangle relationship between \( x \) and \( \theta \).
Why is it necessary to draw a triangle to solve the problem?
-Drawing a triangle helps to visualize the trigonometric relationships and to find the necessary substitutions to express the final answer in terms of \( x \), using the Pythagorean theorem to relate the sides of the triangle to \( x \).
What is the significance of the Pythagorean theorem in the context of this problem?
-The Pythagorean theorem is used to find the third side of the triangle, which is necessary for the substitution back to \( x \) in the final antiderivative expression.

Outlines

00:00

📝 Introduction to Antiderivatives and Completing the Square

In this introductory section, the instructor welcomes viewers back and sets the stage for finding an antiderivative of the function 1/(x^2 - 8x + 1). The method of completing the square is introduced as the primary technique to tackle this problem. Key steps include understanding the necessity of a perfect square and adjusting constants accordingly.

05:01

🔍 Detailed Process of Completing the Square

This paragraph delves into the specific steps of completing the square for the given quadratic function. It explains how to transform the expression x^2 - 8x + 1 into a perfect square form, x - 4)^2 - 15, by adding and subtracting the necessary constant. The importance of maintaining equality through these transformations is emphasized.

10:01

📐 Introduction to Trigonometric Substitution

The instructor transitions to using trigonometric substitution to solve the integral with the transformed quadratic in the denominator. The form u^2 - a^2 is identified, leading to the substitution of u = sqrt(15) sec(theta). The rationale behind this substitution is discussed, highlighting its potential to simplify the integral.

🔄 Substitution and Simplification Steps

This section covers the substitution steps, where x - 4 is replaced by sqrt(15) sec(theta), leading to simplifications involving trigonometric identities. The process includes expressing dx in terms of d(theta) and transforming the integral into one involving secant and tangent functions.

📊 Solving the Integral with Trigonometric Functions

The integral is further simplified by using trigonometric identities and properties of secant and tangent functions. The instructor explains how to break down the expression and find the antiderivative of cosecant(theta). Key trigonometric identities and their applications are highlighted.

🖼️ Using a Triangle for Substitution

The instructor demonstrates how to convert the result back to the variable x using a right triangle based on the substitution x - 4 = sqrt(15) sec(theta). This involves determining the sides of the triangle and using the Pythagorean theorem to find the relationship between x and theta.

🔙 Recap and Final Steps

The final paragraph summarizes the entire process, reiterating the steps of completing the square, making the trigonometric substitution, and using a triangle to revert to the original variable. The importance of each step and the reasoning behind the approach are reviewed to reinforce understanding.

Mindmap

Keywords

💡Antiderivative

An antiderivative is a function that reverses the process of differentiation. In the video, the goal is to find an antiderivative of the function 1/(x^2 - 8x + 1), meaning a function whose derivative is 1/(x^2 - 8x + 1). This concept is central to the video's theme of integral calculus.

💡Completing the square

Completing the square is a technique used to convert a quadratic expression into a perfect square trinomial. In the video, this method is used to transform the denominator x^2 - 8x + 1 into (x - 4)^2 - 15, making it easier to apply further calculus techniques.

💡Trig substitution

Trig substitution is a method used in calculus to simplify integrals by substituting a trigonometric function for a variable. In the video, it involves substituting x - 4 with √15 sec(θ) to transform the integral into one involving trigonometric functions, which are easier to integrate.

💡Secant

Secant (sec) is a trigonometric function defined as the reciprocal of cosine. In the video, the substitution x - 4 = √15 sec(θ) is used, connecting the algebraic expression to trigonometric functions to facilitate integration.

💡Tangent

Tangent (tan) is a trigonometric function defined as the ratio of sine to cosine. The video mentions the identity sec^2(θ) - 1 = tan^2(θ), which helps simplify the integral after the trig substitution is made.

💡Derivative

A derivative represents the rate at which a function is changing at any given point. In the video, the antiderivative found is checked by taking its derivative to see if it returns the original function 1/(x^2 - 8x + 1).

💡Integral

An integral is a fundamental concept in calculus representing the area under a curve. The video focuses on finding the integral (antiderivative) of 1/(x^2 - 8x + 1), which involves several techniques like completing the square and trig substitution.

💡Pythagorean identity

The Pythagorean identity in trigonometry states that 1 + tan^2(θ) = sec^2(θ). This identity is used in the video to simplify the denominator after the trig substitution, turning sec^2(θ) - 1 into tan^2(θ).

💡Theta

Theta (θ) is a variable commonly used to represent an angle in trigonometry. In the video, θ is introduced through the trig substitution x - 4 = √15 sec(θ), linking the problem to trigonometric identities and functions.

💡Trigonometric functions

Trigonometric functions (sine, cosine, tangent, etc.) are used to relate the angles of a triangle to its side lengths. The video applies these functions in the trig substitution method to simplify and solve the integral.

Highlights

Introduction to the task of finding an antiderivative of a given function using the technique of completing the square.

Explanation of the method to verify the antiderivative by differentiating it back to the original function.

Demonstration of completing the square on a quadratic function.

Step-by-step guide to finding the perfect square and adjusting the equation accordingly.

Clarification on the process of adding and subtracting constants to complete the square.

Introduction to the trig substitution method for solving integrals.

Explanation of the trigonometric substitution formula and its application.

Transformation of the integral into a form that allows for trigonometric substitution.

Derivation of the relationship between secant and tangent for the purpose of integration.

Use of trigonometric identities to simplify the integral's denominator.

Substitution of trigonometric functions into the integral and simplification.

Finding the differential dx in terms of trigonometric functions.

Rewriting the integral with trigonometric functions and simplifying the expression.

Integration of trigonometric functions and the use of cosecant for the antiderivative.

Strategy for finding the antiderivative of cosecant theta and relating it to the original function.

Final step of substituting back in terms of x using a triangle representation.

Summary of the entire process from completing the square to trig substitution and final substitution.

Transcripts

Browse More Related Video

Integrals: Trig Substitution 1

Integrals: Trig Substitution 3 (long problem)

Lec 28 | MIT 18.01 Single Variable Calculus, Fall 2007

Unit VI: Lec 1 | MIT Calculus Revisited: Single Variable Calculus

Trigonometric Substitution

Integration Practice I | MIT 18.01SC Single Variable Calculus, Fall 2010