Fundamental Theorem of Calculus 1 | Geometric Idea + Chain Rule Example
TLDRThe video script delves into the Fundamental Theorem of Calculus, which connects derivatives and integrals, two core concepts in calculus. It explains how the theorem relates the rate of change of an area under a curve (integral) to the slope of the curve (derivative), demonstrating that the derivative of an integral is the integrand itself. The video also illustrates this with an example involving the function e to the square root of x, showcasing the application of the theorem and chain rule.
Takeaways
- 📌 The Fundamental Theorem of Calculus (FTC) is divided into two parts, with Part 1 discussed in the video and Part 2 in the subsequent one.
- 📈 FTC connects the concepts of derivatives and integrals, two core components of calculus, by relating the rate of change (derivatives) to accumulation (integrals).
- 🔍 Derivatives are associated with the slope of a tangent line at a point, while integrals deal with the area under a curve over a certain interval.
- 🌀 The accumulation function, G(x), is a dynamic concept where the integral varies with the value of x, representing the area under the curve from 'a' to 'x'.
- 📂 The derivative of the accumulation function G(x) is found to be the original function F(x), demonstrating that the derivative of the integral from 'a' to 'x' of F(t) dt is simply F(x).
- 🔢 The process of finding G'(x) involves the limit as h approaches 0, and the subtraction of two accumulation functions, leading to the integral from 'x' to 'x+h'.
- 📐 The fundamental theorem of calculus requires that the function F(x) be continuous on the interval from 'a' to 'B'.
- 🔄 The video provides an example of using FTC with a composite function, G(x^3), by applying the chain rule to find the derivative of the composite function.
- 🧩 The example illustrates the process of breaking down complex derivatives into manageable parts using the FTC and chain rule.
- 🎓 Understanding the FTC is crucial for grasping the relationship between differentiation and integration, which are fundamental to calculus.
Q & A
What is the main idea behind the Fundamental Theorem of Calculus?
-The main idea behind the Fundamental Theorem of Calculus is to relate derivatives and integrals, two key concepts in calculus, by showing how the derivative of an integral from a to x is equal to the integrand evaluated at x.
What do derivatives and integrals represent in terms of geometry?
-Derivatives represent the slope of a tangent line at a point, while integrals, specifically definite integrals, represent the area under a curve over a specified interval.
How does the Fundamental Theorem of Calculus connect the concepts of derivatives and integrals?
-The Fundamental Theorem of Calculus connects derivatives and integrals by stating that the derivative of an integral from a to x, which is a function G(x), is equal to the integrand F(t) evaluated at x, represented as f(x).
What is the geometric interpretation of the accumulation function G(x)?
-The accumulation function G(x) represents the area under the curve from a to x, which changes dynamically as x varies.
How does the area calculated by the accumulation function G(x) change as x increases?
-As x increases, the area calculated by the accumulation function G(x) also increases, assuming the integrand F(t) is positive. If F(t) is negative, the function G(x) would start decreasing as it accumulates negative areas from beneath the x-axis.
What is the significance of the variables a, x, and t in the context of the Fundamental Theorem of Calculus?
-In the context of the Fundamental Theorem of Calculus, 'a' is a fixed lower limit of integration, 'x' is the variable upper limit, and 't' is a dummy variable representing the integration variable in the integral.
How does the Fundamental Theorem of Calculus relate to the concept of limits in calculus?
-The Fundamental Theorem of Calculus uses the concept of limits to define the derivative of the accumulation function G(x), which is the limit as h approaches 0 of the difference quotient [G(x+h) - G(x)]/h.
What is the process to find the derivative of the accumulation function G(x)?
-To find the derivative of G(x), one calculates the limit as h approaches 0 of [G(x+h) - G(x)]/h, which, through the process of approximation and simplification, results in f(x), the integrand evaluated at x.
What is the assumption made by the Fundamental Theorem of Calculus about the function f?
-The assumption made by the Fundamental Theorem of Calculus is that the function f must be continuous on the interval from a to B, where B is greater than a and x is any value within that interval.
How can the Fundamental Theorem of Calculus be applied to find the derivative of a composite function?
-The Fundamental Theorem of Calculus can be applied to find the derivative of a composite function by using the chain rule, which involves taking the derivative of the outer function evaluated at the inner function, and then multiplying by the derivative of the inner function.
Can you provide an example of applying the Fundamental Theorem of Calculus to a non-standard integral?
-Yes, for example, to find the derivative with respect to x of the integral from 7 to x cubed of e to the square root t dt, one would use the chain rule to treat the integral as a composite function of G(x) and x cubed, apply the Fundamental Theorem of Calculus to find G'(x), and then compose it with x cubed to get the final result, which is 3x squared times e to the square root of x cubed.
Outlines
📚 Introduction to the Fundamental Theorem of Calculus
This paragraph introduces the concept of the Fundamental Theorem of Calculus (FTC) and sets the stage for its explanation. It highlights the importance of the theorem by emphasizing its role in connecting the two main components of calculus: derivatives and integrals. The explanation begins with a discussion of geometric concepts such as the slope of a tangent line (derivatives) and the area under a curve (integrals). The paragraph also introduces the idea of an accumulation function, G(x), which represents the area under the curve from a fixed point 'a' to a variable point 'x'. The dynamic nature of G(x) as a function is explored, and the distinction between the fixed value 'a' and the variable 'x' is clarified. The paragraph concludes by setting up the context for the next part of the explanation, which will delve into the relationship between G(x) and its derivative, G'(x).
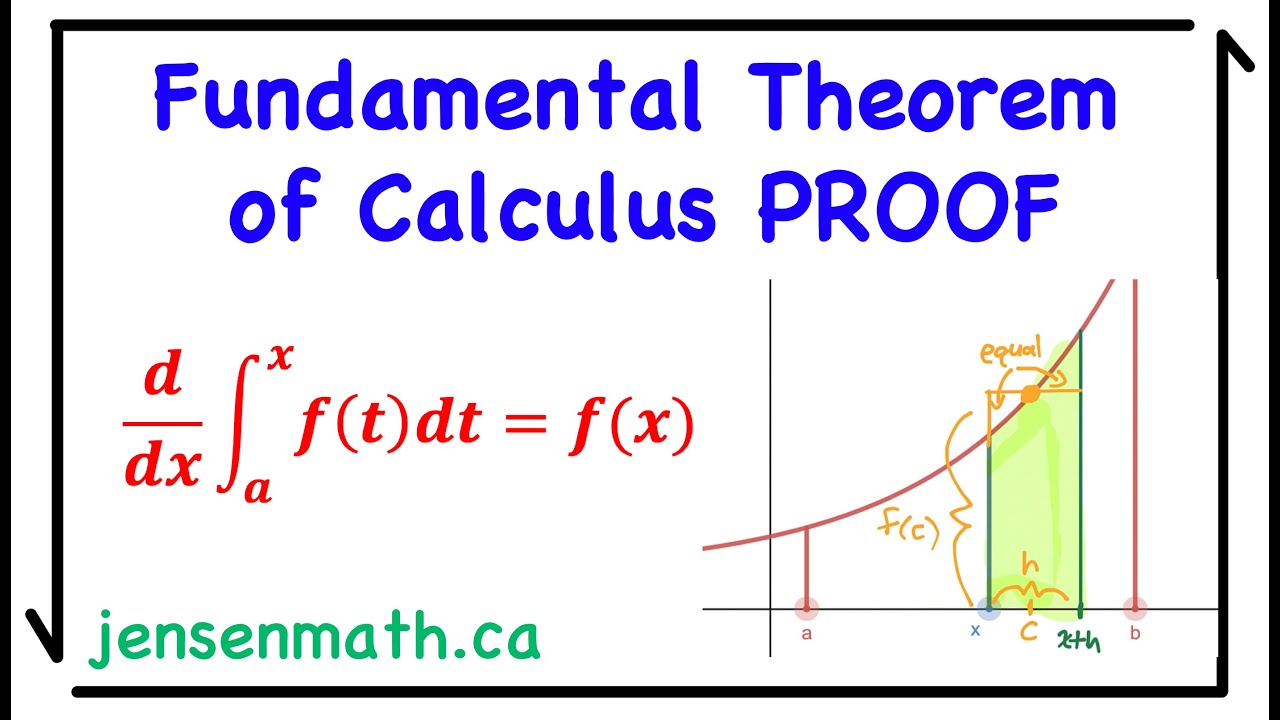
📈 Derivation of the Fundamental Theorem of Calculus
This paragraph delves into the mathematical derivation of the first part of the Fundamental Theorem of Calculus. It begins by visually representing the difference between two accumulation functions and approximating this difference as a rectangle with a fixed height, which is the integral from X to X+h of F(x)dx. The paragraph then connects this approximation to the definition of the derivative, leading to the conclusion that the derivative of the accumulation function G(x) is equal to the integrand F(x). This establishes the first part of the FTC, which states that the derivative of the integral from 'a' to 'x' of F(x)dx is simply F(x). The theorem's assumption of the continuity of the function F(x) on the interval 'a' to 'B' is also mentioned. The paragraph concludes by applying the theorem to a specific example, demonstrating how the FTC can be used to find the derivative of a function.
🔄 Application of the Fundamental Theorem of Calculus with Chain Rule
The final paragraph discusses the application of the Fundamental Theorem of Calculus in a more complex scenario involving the chain rule. It explains how to handle a situation where the theorem's direct application is not immediately possible due to the presence of an additional function, such as X cubed, in the integral. The paragraph outlines the process of using the chain rule to differentiate the composite function G(X cubed), which involves taking the derivative of the outer function G at the inner function X cubed and multiplying it by the derivative of the inner function. The paragraph then applies the FTC to find the derivative of G(X cubed), resulting in the expression e^(√x) multiplied by 3x^2. This example illustrates the flexibility and power of the FTC in combination with other calculus concepts.
Mindmap
Keywords
💡Calculus
💡Derivatives
💡Integrals
💡Fundamental Theorem of Calculus
💡Accumulation Function
💡Geometric Concepts
💡Chain Rule
💡Continuous Function
💡Limit
💡Approximation
Highlights
The Fundamental Theorem of Calculus is introduced, emphasizing its significance in relating derivatives and integrals.
Derivatives are discussed in terms of the slope of a tangent line at a point, while integrals are related to the area under a curve.
The theorem connects two different geometric concepts within calculus: derivatives and integrals.
The concept of an accumulation function, G(x), is introduced as a function that changes with variable x.
The accumulation function G(x) is described as increasing when the function F is positive and decreasing when F is negative.
The philosophical difference between the variables 'a' and 'x' in the accumulation function is explained.
The 't' variable is described as a dummy variable used in the computation of the integral's area.
The process of finding the derivative of the accumulation function G(x) is detailed.
A geometric interpretation of the difference between two accumulation functions is provided.
The approximation of the area between two accumulation functions as a rectangle is discussed.
The derivative of the accumulation function is shown to be equal to the original function F(x).
The Fundamental Theorem of Calculus Part 1 is stated as the derivative of the accumulation function being equal to the integrand F(x).
The theorem's assumption requiring the original function f to be continuous on the interval [a, B] is mentioned.
An example is provided to demonstrate the application of the Fundamental Theorem of Calculus.
The example involves the use of the chain rule to handle a composition of functions.
The final result of the example demonstrates the power of the theorem in simplifying complex derivatives.
Transcripts
Browse More Related Video

Fundamental theorem of calculus (Part 1) | AP Calculus AB | Khan Academy

Calculus 1 - Integration: Proof of the Fundamental Theorem of Calculus

Derivatives of Integrals (w/ Chain Rule)
1st Fundamental Theorem of Calculus PROOF | Calculus 1 | jensenmath.ca

Why Are Slope and Area Opposite: The Fundamental Theorem of Calculus

Calculus AB/BC – 6.7 The Fundamental Theorem of Calculus and Definite Integrals
5.0 / 5 (0 votes)
Thanks for rating: