GCSE Physics Revision "Forces and Elasticity"

Freesciencelessons
13 Feb 201804:12
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, viewers learn the distinction between elastic and inelastic deformation, and how to calculate the force necessary to stretch or compress an object. Elastic materials, such as a slinky or rubber bands, return to their original shape after the force is removed, while inelastic materials do not. The video introduces the formula for calculating the force on an elastic object and explains the concept of elastic potential energy. It encourages viewers to practice these concepts and consult the accompanying workbook for further understanding.

Takeaways
  • 📚 The difference between elastic and inelastic deformation is a key concept.
  • 🏗️ Elastic materials return to their original length or shape after forces are removed, while inelastic materials do not.
  • 🔍 Examples of elastic materials include slinky, rubber bands, rubber gloves, and clay.
  • 🤔 Elastic deformation involves stretching, compressing, or bending with forces that are balanced and opposite in direction.
  • 🚫 Inelastic materials, such as certain polymers, do not return to their original shape after deformation.
  • 📐 To calculate the force needed to stretch or compress an elastic object, use Hooke's Law: Force (N) = Spring Constant (N/m) × Extension/Compression (m).
  • 📝 The equation for Hooke's Law is essential to learn for exams and practical applications.
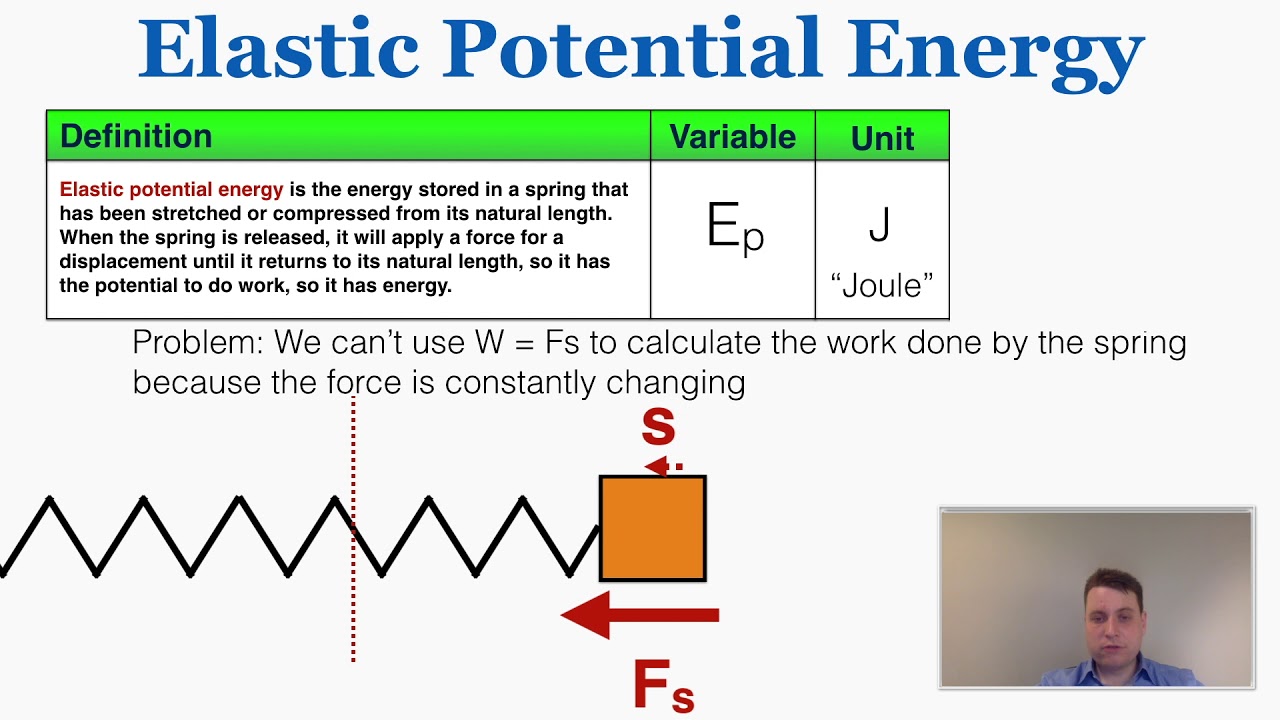
  • 🔄 When an elastic object is stretched or compressed, elastic potential energy is stored in the object.
  • 🌟 The work done in stretching or compressing an elastic object is equal to the elastic potential energy stored.
  • 📚 Further exploration of elastic potential energy and its applications is recommended through additional resources.
  • 🔗 Access to practice questions and a workbook on forces and elasticity is available through provided links.
Q & A

  • What are the two types of deformation discussed in the video?

    -The two types of deformation discussed are elastic deformation and inelastic deformation.

  • What is the defining characteristic of elastic materials?

    -Elastic materials return to their original length or shape when the forces acting on them are removed.

  • How many forces are typically required to change an object's length or shape?

    -More than one force is required to change an object's length or shape to ensure the forces are balanced.

  • What happens when an inelastic material is stretched?

    -An inelastic material does not return to its original length when the forces are removed after stretching.

  • What is the formula used to calculate the force needed to stretch an elastic object?

    -The formula is F = k * x, where F is the force in Newtons, k is the spring constant in Newtons per meter, and x is the extension in meters.

  • What is the term for deformation that involves a change in shape but not length?

    -The term for such deformation is bending.

  • What type of energy is stored in an elastic object when it is stretched or compressed?

    -Elastic potential energy is stored in the object when it is stretched or compressed.

  • How can you calculate the compression force on an elastic object?

    -The compression force can be calculated using the same formula as for stretching, but the term e represents compression instead of extension.

  • What is the relationship between the work done and the elastic potential energy stored?

    -The work done is equal to the elastic potential energy stored in the object, provided the object is not in an elastically deformed state.

  • What is the spring constant mentioned in the video, and what is its unit?

    -The spring constant mentioned is 200 Newtons per meter (N/m).

  • How can you find additional practice questions on forces and elasticity?

    -You can find additional practice questions on forces and elasticity in the presenter's workbook, accessible via the provided link.

Outlines
00:00
🎓 Introduction to Elastic and Inelastic Deformation

This paragraph introduces the concepts of elastic and inelastic deformation, setting the stage for the lesson. It explains that by the end of the video, viewers should understand the difference between the two types of deformation and be able to calculate the force required to stretch or compress an object. It also mentions the energy transfers involved when an elastic object undergoes stretching, compression, or bending. The paragraph presents various examples of elastic materials such as a slinky, rubber bands, rubber gloves, an eraser, a clay ground surface, and a tennis ball, and explains that elastic materials return to their original length or shape once the forces acting on them are removed.

Mindmap
Keywords
💡Elastic Deformation
Elastic deformation refers to the change in shape or length of a material under stress that is reversible when the stress is removed. In the video, this concept is illustrated by objects such as a slinky, rubber bands, and rubber gloves, which return to their original shape after being stretched or compressed. The key fact highlighted is that elastic materials always return to their original length or shape when the forces are removed, which is a fundamental characteristic of elastic materials and a central theme of the video.
💡Inelastic Deformation
Inelastic deformation is the permanent change in shape or size of a material when a force is applied, and the material does not return to its original state once the force is removed. The video contrasts this with elastic deformation, using certain polymers as an example of inelastic materials. This concept is crucial for understanding the difference between materials that can return to their original form and those that cannot, which is a key point in the discussion of material properties and deformation in the video.
💡Force
In the context of the video, force is the push or pull applied to an object that can cause it to change its shape, size, or motion. It is a fundamental concept in physics and is used to explain how objects like rubber bands or springs respond to stress. The video specifically discusses how to calculate the force needed to stretch or compress an elastic object, using the formula F = k * x, where F is the force in Newtons, k is the spring constant, and x is the extension or compression in meters. This formula is essential for understanding the relationship between force and deformation in elastic materials.
💡Spring Constant
The spring constant, often denoted as k, is a measure of the stiffness of a spring. It is defined as the force needed to extend or compress the spring by a unit length, typically in Newtons per meter (N/m). In the video, the spring constant is used in the formula to calculate the force required to stretch or compress an elastic object. A higher spring constant indicates a stiffer spring, which requires more force to achieve the same extension or compression. This concept is central to understanding how springs and other elastic materials respond to different forces.
💡Energy Transfers
Energy transfers refer to the movement of energy from one form to another or from one object to another. In the context of the video, when an elastic object is stretched, compressed, or bent, it undergoes elastic deformation, and during this process, energy is transferred in the form of work done on the object. This energy is stored as elastic potential energy within the object. The video emphasizes that the work done is equal to the elastic potential energy, which is a critical concept for understanding how energy is conserved and transformed in elastic deformation scenarios.
💡Elastic Potential Energy
Elastic potential energy is the energy stored in an elastic object when it is stretched, compressed, or deformed in any way. In the video, it is explained that when an elastic object is deformed, work is done on the object, and this work is stored as elastic potential energy. The concept is central to understanding the energy dynamics involved in the deformation of materials. The video also mentions that this energy is only conserved if the object is not in an elastically deformed state, which is an important nuance in the study of energy transformations.
💡Extension
Extension, as used in the video, refers to the increase in length of an elastic object when a force is applied to it, causing it to stretch. The video provides a formula to calculate the force needed to cause this extension, which is a fundamental concept in understanding how much force is required to achieve a certain degree of deformation in elastic materials. The term is used in the context of the spring constant formula, where the extension (x) is a necessary value to determine the force (F) needed to stretch the spring or other elastic objects.
💡Compression
Compression in the video refers to the decrease in volume or length of an elastic object when a force is applied, causing it to squeeze or contract. This concept is used to describe the behavior of elastic materials when subjected to inward forces, as opposed to extension, which involves stretching. The video explains that the same formula used for calculating the force needed to stretch an object (F = k * x) can also be applied to calculate the force needed for compression, with 'e' standing for compression instead of extension. This understanding is crucial for analyzing the behavior of materials under different types of stress.
💡Bending
Bending, as discussed in the video, is a type of deformation where an elastic object is subjected to forces that cause it to curve or change its shape without stretching or compressing uniformly. The video uses the example of applying three forces to an elastic material, causing it to bend. Bending is one of the ways in which elastic materials can undergo deformation, and it is important to understand because it is one of the scenarios where energy transfer and storage as elastic potential energy occur, as long as the object returns to its original shape after the forces are removed.
💡Balanced Forces
Balanced forces are forces that are equal in magnitude but opposite in direction, resulting in no net force and therefore no change in the motion or shape of an object. In the video, this concept is used to explain that when elastic materials are stretched or compressed, the forces applied at either end are balanced, which means they cancel each other out. This balance is crucial for the object to return to its original shape after the forces are removed, which is a characteristic of elastic deformation.
💡Work Done
In the context of the video, work done refers to the energy transferred to or from an object when a force is applied over a distance. Specifically, when an elastic object is stretched or compressed, the work done on the object is equal to the change in elastic potential energy. This concept is important for understanding the energy dynamics involved in deformation, as it highlights the conservation of energy principle, where the work done on the object is stored as potential energy within the object until it is released or the object returns to its original shape.
Highlights

The video introduces the concepts of elastic and inelastic deformation.

Elastic materials return to their original length or shape after the forces are removed.

Inelastic materials do not return to their original length when the forces are removed.

An elastic material requires more than one force to change its length or shape.

The stretching forces on an elastic material are equal in magnitude and opposite in direction.

Compression forces on an elastic material cause it to compress and return to its original length when removed.

Elastic deformation occurs when an object bends and returns to its original shape and length after force removal.

The formula to calculate the force needed to stretch an elastic object is F = k * x, where F is the force in Newtons, k is the spring constant in Newtons per meter, and x is the extension in meters.

An example calculation is provided to extend a spring by 0.04 meters with a spring constant of 200 Newtons per meter, resulting in a force of 8 Newtons.

The same formula can be used to calculate compression forces on an elastic object.

Elastic potential energy is stored in an object when it is stretched, compressed, or bent.

The work done in stretching or compressing an elastic object is equal to the elastic potential energy stored.

A practical on stretching a spring is mentioned as part of the content for further study.

The video encourages viewers to practice with the provided example and seek additional resources in the workbook.

Elastic potential energy was previously introduced in the energy topic, and the video suggests revisiting that content.

The video concludes with a teaser for the next topic, which will delve into the practical aspects of stretching a spring.

Transcripts

Browse More Related Video

(previous version) Introduction to Elastic Potential Energy with Examples

GCSE Physics - Elasticity, spring constant, and Hooke's Law #44

Introduction to Elastic and Inelastic Collisions

Introduction to Elastic Potential Energy with Examples

Differentiating Between Elastic and Inelastic Collisions | Physics in Motion

Elastic Potential Energy - IB Physics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsEducationElasticityDeformationForceCalculationMaterialScienceSpringConstantEnergyTransferPracticalApplicationEducationalContentScientificConcepts