(previous version) Introduction to Elastic Potential Energy with Examples

Flipping Physics
7 Dec 201507:17
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the concept of elastic potential energy, a type of energy stored in an object due to its temporary deformation. It uses examples like springs, rubber bands, and a Slinky to illustrate how this energy is stored and converted to kinetic and gravitational potential energy. The script also explains the equation for calculating elastic potential energy, which involves the spring constant (k) and displacement (x), and emphasizes the linear relationship between the force exerted by a spring and its displacement, as described by Hooke's Law. The video concludes with a practical example of determining the spring constant of a rubber band and calculating the energy stored when it is stretched.

Takeaways
  • 📌 Elastic potential energy (PE) is represented as PE_e or U_e, denoting its association with elastic deformation.
  • 🔄 Elastic potential energy is the energy stored in an object due to its temporary deformation, such as in a spring when compressed or elongated.
  • 🌐 Examples of elastic potential energy include springs, rubber bands, and toys like Slinkies and Pogo sticks.
  • ⚖️ The equation for elastic potential energy is PE = (1/2)kx^2, where k is the spring constant and x is the displacement from the equilibrium position.
  • 📈 The spring constant (k) measures the amount of force needed to displace a spring per meter, with higher values indicating stiffer springs.
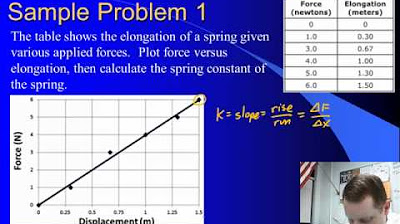
  • 🔢 Spring constants can be determined experimentally by measuring the force and displacement, as demonstrated with a rubber band having a spring constant of 241 N/m.
  • 🔄 Displacement from the equilibrium position can be negative, but since it is squared in the formula, elastic potential energy cannot be negative.
  • 💡 Elastic potential energy can be converted into kinetic and gravitational potential energy, as seen when a compressed object is released.
  • 📚 Like kinetic and gravitational potential energy, elastic potential energy is a scalar quantity.
  • 🤓 The concepts discussed are based on principles of physics, such as Hooke's Law, which relates the force exerted by a spring to its displacement.
Q & A

  • What is the symbol for elastic potential energy?

    -The symbol for elastic potential energy is PE with a subscript of 'e', sometimes denoted as U with a subscript of 'e'.

  • What is elastic potential energy?

    -Elastic potential energy is the energy stored in an object due to its temporary deformation, such as when a spring is compressed or elongated.

  • How can elastic potential energy be converted?

    -Elastic potential energy can be converted to kinetic energy and gravitational potential energy, as seen when a compressed spring is released or a ball regains its shape after striking the ground.

  • What are some examples of objects that store elastic potential energy?

    -Examples include springs, rubber bands, and rubber balls. These objects store elastic potential energy when they are temporarily deformed, such as being stretched, compressed, or bent.

  • What is the equation for elastic potential energy?

    -The equation for elastic potential energy is PE = (1/2)kx^2, where 'k' is the spring constant and 'x' is the displacement from the equilibrium position.

  • What are the dimensions of the spring constant 'k'?

    -The spring constant 'k' typically has dimensions of newtons per meter (N/m), indicating the force required to displace the spring by a meter.

  • How does the spring constant relate to the force and displacement of a spring?

    -The spring constant is a measure of the force needed to compress or expand the spring per meter of displacement. A higher spring constant means more force is required for the same displacement.

  • How can you determine the spring constant of a rubber band?

    -The spring constant of a rubber band can be determined by measuring the force and displacement during an experiment, and then calculating the slope of the resulting force-displacement graph.

  • What is the unit for elastic potential energy?

    -The unit for elastic potential energy is joules (J), which is derived from the units of the spring constant (newtons per meter) and displacement (meters).

  • Is it possible to have negative elastic potential energy?

    -No, elastic potential energy cannot be negative because the displacement from the rest position, although it can be negative, is squared in the formula, resulting in a positive value.

  • What is the significance of the spring constant in the context of Hooke's Law?

    -Hooke's Law states that the force exerted by a spring is proportional to the displacement from its equilibrium position, with the spring constant 'k' being the constant of proportionality. It describes the stiffness of the spring.

  • How does the scalar nature of elastic potential energy affect its calculation?

    -As a scalar, elastic potential energy only has magnitude and no direction, which means that its calculation is straightforward and does not involve vector components, simplifying the process.

Outlines
00:00
🌟 Elastic Potential Energy Basics

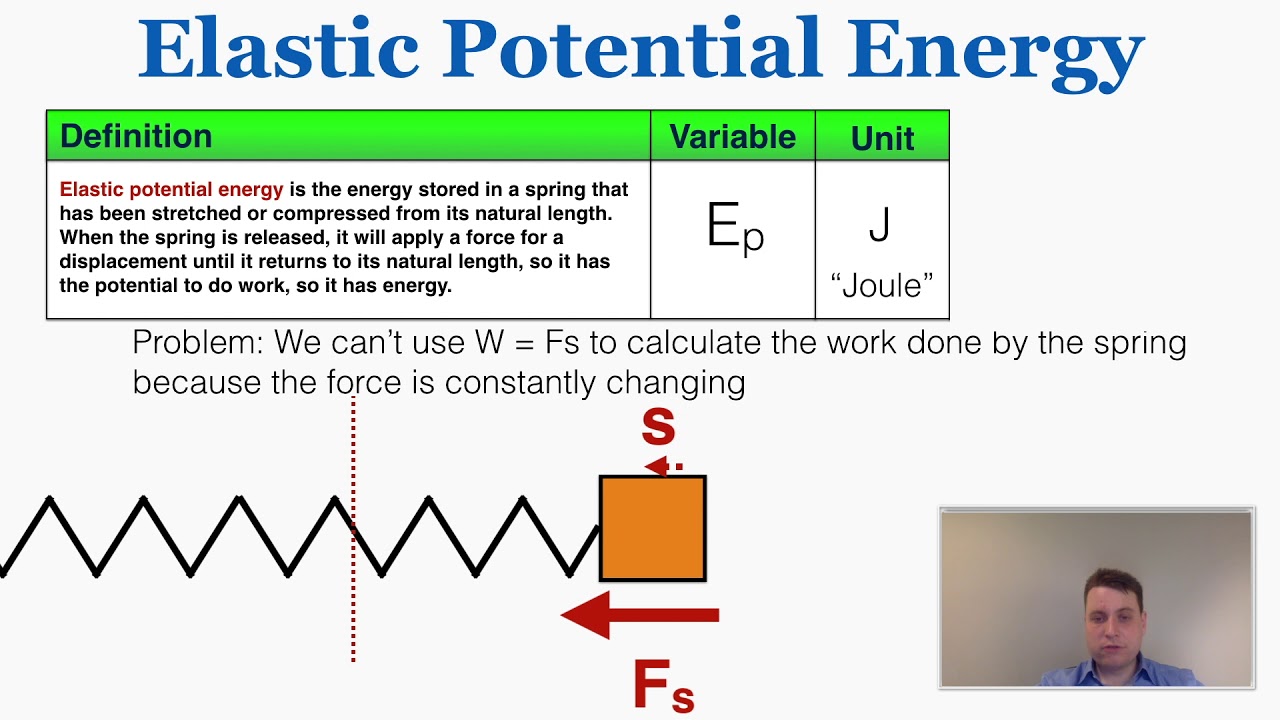
This paragraph introduces the concept of elastic potential energy, denoted as PE with a subscript 'e', and its alternative representation as U with a subscript 'e'. It explains that elastic potential energy is the energy stored in an object due to its temporary deformation, with springs being a common example. The paragraph also mentions other objects like toys and rubber bands that store this type of energy. The equation for elastic potential energy is given as (1/2)kx^2, where 'k' is the spring constant with units of newtons per meter, and 'x' is the displacement from the equilibrium position. The importance of the spring constant in determining the force required to compress or expand a spring is discussed, along with examples of springs with different spring constants. The Slinky and Pogo stick are used to illustrate the concept of spring constant, and an example is provided to calculate the elastic potential energy stored in a rubber band.

05:01
📚 Calculation of Elastic Potential Energy

This paragraph focuses on the calculation of elastic potential energy using the formula (1/2)kx^2. It involves a practical example where a rubber band is stretched to determine its spring constant and the energy stored when it is elongated by 12 centimeters or 0.12 meters. The calculation results in an energy value of 1.7 joules, highlighting the units of newtons per meter and meters squared leading to joules. The paragraph also touches on the nature of elastic potential energy as a scalar quantity, and the impossibility of having negative elastic potential energy due to the squaring of the displacement from the rest position. The contribution of Mr. Fullerton from APlusPhysics in explaining the concept is acknowledged.

Mindmap
Keywords
💡Elastic Potential Energy
Elastic potential energy refers to the stored energy in an object due to its temporary deformation, such as stretching or compressing. In the video, this concept is exemplified by the deformation of a spring or a rubber band, which stores energy that can be converted into kinetic or gravitational potential energy. The formula for calculating elastic potential energy is also discussed, which is one half k times x-squared, where k is the spring constant and x is the displacement from the equilibrium position.
💡Spring Constant (k)
The spring constant, denoted as k, is a measure of the stiffness of a spring. It quantifies the amount of force required to displace the spring by a certain distance. In the video, it is explained that a larger spring constant indicates a stiffer spring, requiring more force to achieve the same displacement. The units for the spring constant are newtons per meter.
💡Hooke's Law
Although not explicitly defined in the video, Hooke's Law is implied as the principle that describes the linear relationship between the force exerted by a spring and its displacement from the equilibrium position. The law is mathematically expressed as F = -kx, where F is the force exerted by the spring, k is the spring constant, and x is the displacement.
💡Displacement
Displacement, in the context of the video, refers to the change in position of an object from its equilibrium or rest position. It is a vector quantity that can be positive or negative, indicating the direction of movement from the equilibrium position. However, since displacement is squared in the formula for elastic potential energy, the value cannot be negative, ensuring that elastic potential energy is always a positive quantity.
💡Kinetic Energy
Kinetic energy is the energy possessed by an object due to its motion. In the video, it is mentioned that the energy stored as elastic potential energy can be converted into kinetic energy. This conversion is demonstrated by the spring or rubber band when they release their stored energy, allowing an object to move.
💡Gravitational Potential Energy
Gravitational potential energy is the energy an object possesses due to its position in a gravitational field, typically as a result of its height above a reference point. In the video, it is mentioned that elastic potential energy can be converted into gravitational potential energy, and vice versa.
💡Equilibrium Position
The equilibrium position, also referred to as the rest position in the video, is the position where the net force on an object is zero, and it is in a state of rest or unstrained. For a spring, this is the position where no external forces are acting upon it, and it is not stretched or compressed.
💡Scalar
A scalar is a quantity that has magnitude but no direction. In the context of the video, elastic potential energy is mentioned as being a scalar, meaning it only has a size or amount, but does not have a directional component.
💡Force Sensor
A force sensor is a device used to measure the force applied to it. In the video, a force sensor is used to demonstrate the relationship between the force exerted by a rubber band and its displacement from the equilibrium position.
💡Joules
Joules are the unit of measurement for energy in the International System of Units (SI). They are used to quantify the amount of energy stored or transferred in various forms, such as work, heat, or potential energy. In the video, the unit joules is used to express the calculated elastic potential energy stored in the rubber band.
💡APlusPhysics.com
APlusPhysics.com is a website mentioned in the video that provides educational content related to physics. In the context of the video, Mr. Fullerton, who appears in the video, is associated with this website, suggesting that it is a resource for learning physics concepts.
Highlights

The symbol for elastic potential energy is PE with a subscript of 'e', or sometimes U with a subscript of 'e'.

Elastic potential energy is the energy stored in an object due to its temporary deformation.

Common examples of elastic potential energy include springs and toys like rubber bands and rubber balls.

When a spring is compressed or elongated, elastic potential energy is stored and can be converted to kinetic and gravitational potential energy.

The equation for elastic potential energy is PE_e = (1/2)kx^2, where k is the spring constant and x is the displacement from the equilibrium position.

The spring constant measures how much a spring resists displacement and is expressed in newtons per meter.

Different springs have different spring constants; a weak spring has a small spring constant, while a strong spring has a large one.

The Slinky and Pogo stick are examples of objects that can be analyzed for their spring constant.

The rubber band's spring constant was determined to be 241 newtons per meter through experimentation.

Elastic potential energy stored in a rubber band can be calculated using the formula, with the rubber band's elongation providing the displacement value.

The units for elastic potential energy are joules, derived from the units of the spring constant and displacement.

Elastic potential energy, like kinetic and gravitational potential energy, is a scalar quantity.

Negative displacement from the rest position is possible, but since it is squared in the formula, elastic potential energy cannot be negative.

The concept of elastic potential energy and its relation to other forms of energy is a fundamental topic in physics.

Understanding the relationship between force, displacement, and energy is crucial for analyzing systems involving elastic potential energy.

Experimental methods, such as using a force sensor, can be employed to measure the spring constant and calculate elastic potential energy.

Transcripts

Browse More Related Video

Introduction to Elastic Potential Energy with Examples

High School Physics - Springs and Hooke's Law

Elastic Potential Energy - IB Physics

Potential energy stored in a spring | Work and energy | Physics | Khan Academy

Simple Harmonic Motion, Mass Spring System - Physics Full Topic

GCSE Physics - Elastic Potential Energy and F = ke Equations #45

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsEducationElasticEnergySpringConstantHookesLawMechanicalEnergySTEMLearningInteractiveExamplesAPlusPhysicsEnergyConversionScalarQuantities