Confidence Interval Concept Explained | Statistics Tutorial #7 | MarinStatsLectures

MarinStatsLectures-R Programming & Statistics
3 Jul 201808:15
EducationalLearning
32 Likes 10 Comments

TLDRThis video delves into the concept of sampling distribution and its role in constructing confidence intervals, particularly for a single mean. It explains how, under certain conditions, the sample mean follows an approximately normal distribution centered around the true population mean. The video uses the example of systolic blood pressure to illustrate how a sample mean is likely to fall within two standard deviations of the true mean with a 95% confidence interval. It emphasizes the practical application of these concepts when the true population parameters are unknown, and we rely on sample data to make inferences about the population. The video also touches on the transition from using Z-scores to t-values when the population standard deviation is unknown, setting the stage for a deeper discussion on confidence intervals in subsequent videos.

Takeaways
  • ๐Ÿ“Š The concept of a sampling distribution is crucial for building confidence intervals, particularly for a single mean.
  • ๐Ÿง  Understanding sample estimates' behavior in relation to the true population parameters is fundamental when the population parameters are known.
  • ๐Ÿ’ก The sampling distribution of sample means is approximately normally distributed when certain conditions are met, with the sample mean expected to equal the population mean.
  • ๐Ÿ“ˆ The standard error of the mean (SEM) measures the average distance the sample mean estimate moves away from the true mean and is calculated to be 4 in the given example.
  • ๐Ÿ”ข The 68-95-99.7 rule (empirical rule) states that approximately 95% of sample means fall within two standard deviations of the mean in a normal distribution.
  • ๐Ÿ”ฎ This rule implies that roughly 95% of the time, the true population mean will be within two standard deviations of the sample mean estimate.
  • ๐Ÿค” In practice, we often do not know the true population parameters, so we use sample data to make inferences about the population.
  • ๐Ÿ”„ The idea of 'confidence' in a confidence interval means that if we were to repeat the sampling process, 95% of the time our interval will contain the true population mean.
  • ๐ŸŒ When constructing a confidence interval, we replace the population standard deviation with the sample standard deviation and use a t-value instead of a z-score.
  • ๐Ÿ“ The statement of a confidence interval (e.g., 95% confidence) does not equate to a probability but rather an expression of confidence that the interval overlaps with the true population mean.
Q & A

  • What is the main concept discussed in the video?

    -The main concept discussed in the video is the construction of a confidence interval for a single mean using the idea of a sampling distribution.

  • What is a sampling distribution?

    -A sampling distribution describes all the possible estimates (sample means) that could be obtained from a population by taking random samples under certain conditions.

  • What are the conditions for the sample mean to be approximately normally distributed?

    -The sample mean is approximately normally distributed when the population is large, and the sample size is sufficiently large, typically n โ‰ฅ 30.

  • What is the standard error of the mean?

    -The standard error of the mean is a measure that gives an idea of how much the sample mean is expected to vary from the true population mean, on average.

  • What is the 68-95-99.7 rule?

    -The 68-95-99.7 rule, also known as the empirical rule, states that in a normal distribution, approximately 68% of the data falls within one standard deviation of the mean, 95% within two standard deviations, and 99.7% within three standard deviations.

  • How does the video illustrate the relationship between the sample mean and the population mean?

    -The video illustrates that approximately 95% of the time, the sample mean will be within two standard deviations of the population mean, suggesting that we can estimate the population mean with a certain level of confidence based on the sample mean.

  • Why can't we always know the true mean or standard deviation of a population?

    -In the real world, we often don't have access to the entire population data. Instead, we collect a sample of data and use that to make inferences about the population parameters.

  • What is the significance of the t-value in the context of confidence intervals?

    -The t-value is used in place of the Z-score when the population standard deviation is unknown and is estimated by the sample standard deviation. It accounts for the additional uncertainty in the estimate of the population mean.

  • How does the video explain the concept of confidence in relation to confidence intervals?

    -The video explains that when we construct a confidence interval, we are stating that we are 'x% confident' that the interval contains the true population mean, not that there is an 'x% chance' the true mean is in the interval. This reflects the fact that we can only estimate the population parameters based on our sample data.

  • What is the role of the sample size in determining the precision of the confidence interval?

    -The larger the sample size, the more precise the confidence interval becomes. This is because a larger sample size provides a more accurate estimate of the population parameters and reduces the variability of the sample mean.

  • How does the video relate the concept of confidence intervals to real-world applications?

    -The video emphasizes that in real-world applications, we use sample data to make statements about the population. Confidence intervals provide a range within which we can estimate the population mean with a certain level of confidence, based on our sample data.

Outlines
00:00
๐Ÿ“Š Understanding Sampling Distribution and Confidence Intervals

This paragraph introduces the concept of a sampling distribution and its role in constructing a confidence interval for a single mean. It explains how sample estimates behave when the true population parameters are known, using an example of systolic blood pressure. The discussion focuses on the sampling distribution's approximate normality under certain conditions and introduces the standard error of the mean. The paragraph also delves into the 68-95-99.7 rule, illustrating that 95% of sample means fall within two standard deviations of the population mean. The idea is extended to infer that the population mean is likely within two standard deviations of the sample mean in 95% of the cases.

05:08
๐Ÿ” Generalizing Confidence Intervals and Addressing Real-World Scenarios

The second paragraph discusses the practical application of confidence intervals in situations where the true population mean and standard deviation are unknown. It emphasizes the shift from using the Z-score to the t-score when the population standard deviation is replaced with the sample standard deviation. The paragraph clarifies that confidence intervals do not quantify the probability of the true population mean being within the interval but rather express a level of confidence that the interval contains the population mean. It sets the stage for a deeper exploration of confidence intervals and the T distribution in subsequent content.

Mindmap
Keywords
๐Ÿ’กSampling Distribution
The sampling distribution is a theoretical distribution that describes all possible sample estimates we could obtain from a population. In the video, it is used to illustrate how the sample mean behaves when drawn from a population with a known mean and standard deviation. The concept is crucial for understanding confidence intervals, as it shows the range of possible outcomes when estimating population parameters from samples.
๐Ÿ’กConfidence Interval
A confidence interval is a range within which we expect the true population parameter, such as the mean, to lie with a certain level of confidence. It is based on the sample data and provides an estimate that accounts for the uncertainty of not knowing the true value. The video focuses on building a confidence interval for a single mean, emphasizing the use of the sampling distribution and the standard error of the mean.
๐Ÿ’กStandard Error of the Mean
The standard error of the mean (SEM) is a measure that describes the average amount by which sample means are expected to deviate from the true population mean. It is the standard deviation of the sampling distribution of the sample mean. In the context of the video, the SEM is used to understand the precision of the sample mean as an estimate of the population mean and to calculate the width of the confidence interval.
๐Ÿ’กStandard Deviation
The standard deviation is a statistical measure that quantifies the amount of variation or dispersion in a set of values. In the video, it is used to describe the distribution of the population's systolic blood pressure and later, the distribution of all possible sample means. The standard deviation is a key component in understanding the spread of the sampling distribution and in calculating confidence intervals.
๐Ÿ’กPopulation Mean
The population mean is the average value of a characteristic for an entire population. In statistical analysis, the population mean is the true value that we seek to estimate using sample data. The video discusses how the concept of a confidence interval is used to make inferences about the population mean based on sample statistics.
๐Ÿ’กSample Mean
The sample mean is the average value of a characteristic calculated from a sample of observations drawn from a population. It is used as an estimate of the population mean. The video emphasizes the behavior of the sample mean in the context of the sampling distribution and how it forms the basis for constructing confidence intervals.
๐Ÿ’กEstimate
An estimate is a statistical value derived from sample data that is used to infer information about a population parameter. In the video, the concept of estimation is central to understanding how confidence intervals function, as they provide a range within which the population parameter, like the mean, is estimated to fall.
๐Ÿ’กTrue Distribution
The true distribution refers to the actual distribution of a variable in the entire population. It is the theoretical distribution that we cannot directly observe but can estimate through sampling and statistical analysis. The video uses the concept of the true distribution to contrast the sampling distribution and to illustrate the goal of statistical inference.
๐Ÿ’กTwo Standard Deviations
The term 'two standard deviations' refers to a rule of thumb in statistics that states approximately 95% of the data in a normal distribution falls within two standard deviations of the mean. This concept is used in the video to explain the construction of a 95% confidence interval, where we expect 95% of the sample means to fall within this range of the population mean.
๐Ÿ’กT-Value
The t-value is a statistical measure used in hypothesis testing and the construction of confidence intervals when the population standard deviation is unknown. It is used instead of the Z-score in such cases and is typically larger than two, which is the Z-score associated with the 95% confidence level in a standard normal distribution. The video mentions that the t-value will be discussed in more detail when formally introducing confidence intervals.
๐Ÿ’กConfidence Level
The confidence level, such as 95%, represents the degree of certainty or confidence that we have about a statistical estimate, such as a confidence interval. It indicates the proportion of all possible samples that can be expected to include the true population parameter. In the video, the confidence level is used to discuss the probability that the confidence interval contains the population mean.
Highlights

The video discusses the concept of a sampling distribution and its role in constructing a confidence interval for a single mean.

The example given involves the systolic blood pressure in a population with a known skewed distribution, mean, and standard deviation.

A sample of 25 is taken from the population, and the sample mean is calculated.

The theoretical sampling distribution of all possible sample means is approximately normally distributed when certain conditions are met.

The sample mean is expected to be equal to the true mean of the population, with the standard deviation of the mean referred to as the standard error of the mean.

The video introduces the 68-95-99.7 rule, explaining that approximately 95% of sample means fall within two standard deviations of the mean.

The concept is extended to the idea that 95% of the time, the true mean will be within two standard deviations of the sample mean estimate.

A visual representation is provided to illustrate how the sample means cluster around the true mean.

The video acknowledges the reality that we often do not know the true distribution, mean, or standard deviation of a population.

The usefulness of the sampling distribution is emphasized, even when the true values are unknown.

The video explains the concept of using the sample standard deviation instead of the population standard deviation when estimating the population mean.

The use of t-values instead of z-scores is introduced when the population standard deviation is unknown.

The video clarifies that confidence intervals do not state a probability that the true population mean is within the interval, but rather a level of confidence.

The distinction between probability and confidence in the context of confidence intervals is explained.

The video concludes by stating that more details on confidence intervals will be discussed in future videos.

Transcripts

Browse More Related Video

Introduction to the t Distribution (non-technical)

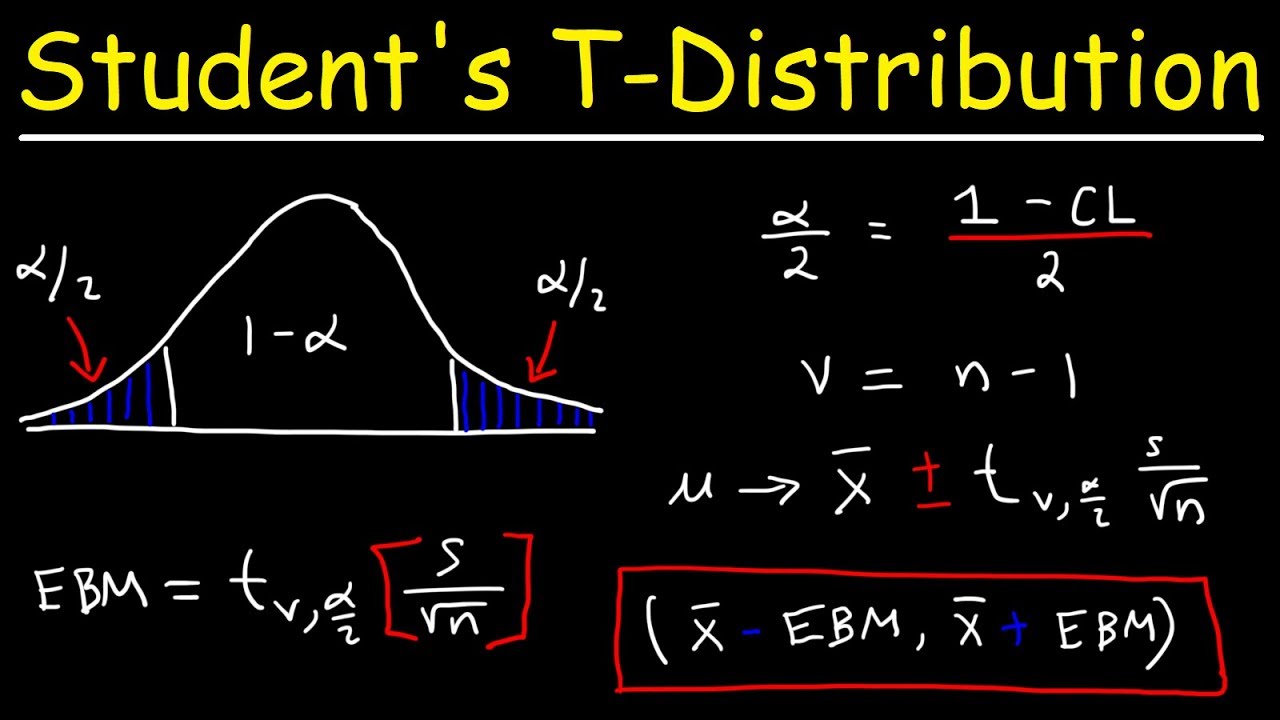
Student's T Distribution - Confidence Intervals & Margin of Error

Confidence Intervals | Population Mean: ฯƒ Unknown

Statistics 101: Confidence Interval Estimation, Sigma Known

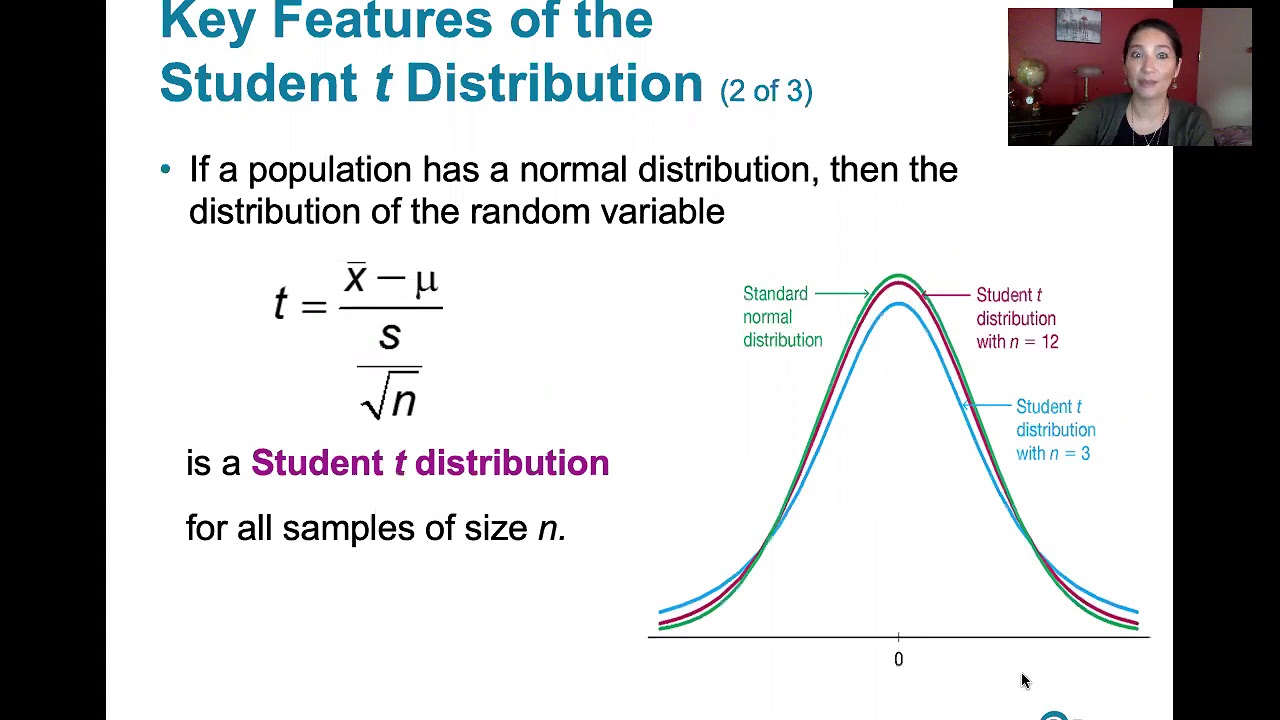
7.2.1 Estimating a Population Mean - Student t Distribution and Finding Critical t Values

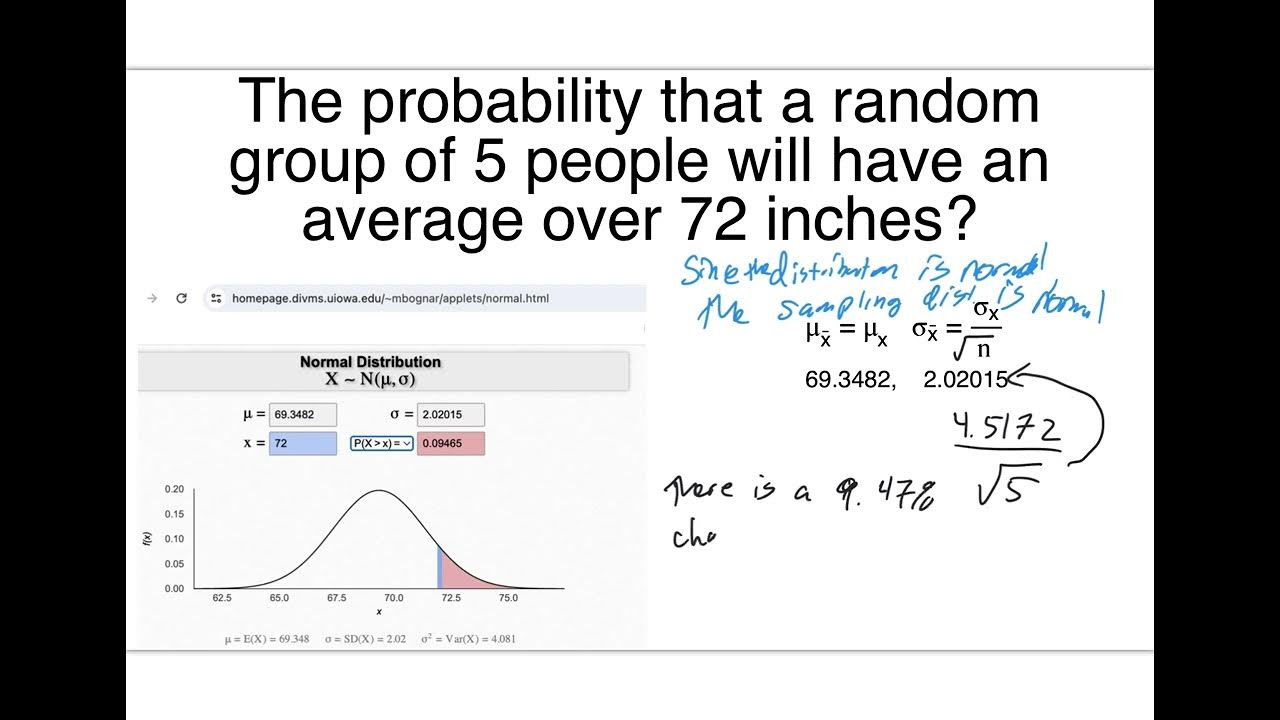
2610 Chapter 8 Day 1

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
StatisticsSampling DistributionConfidence IntervalStandard ErrorPopulation MeanEstimationData AnalysisStatistical ConceptsProbabilityT-Distribution