Understanding Vector Spaces

Professor Dave Explains
12 Mar 201908:41
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational episode, Professor Dave delves into the foundational concept of vector spaces, also known as linear spaces, building upon the previous discussions on vectors, matrices, and basic mathematical operations like addition and scalar multiplication. The video introduces the notation and key properties of vector spaces, including commutativity, associativity, and the existence of a zero vector. It emphasizes the crucial concept of closure, illustrating it through examples with real numbers, real vectors, matrices, and even linear polynomials, thereby demonstrating that vector spaces can encompass a variety of elements beyond just vectors. The episode concludes by exploring what happens when a set doesn't satisfy closure properties, making it clear that not all sets of vectors form a vector space.

Takeaways
  • 😀 A vector space is a set of elements that can be added and multiplied by scalars while satisfying certain properties
  • 😯 Closure is an important property - multiplying an element by a scalar and adding elements must give results still within the set
  • 📚 Examples of vector spaces include sets of vectors, matrices, and linear functions
  • 😮 The set of all real numbers forms a vector space
  • 🤔 A set is not a vector space if the closure properties are not satisfied
  • 👍 Vectors spaces have commutative and associative addition
  • 👍 They contain a zero vector and inverses for each element
  • 👍 Scalars distribute across vector addition and scalar multiplication
  • 🔢 Multiplying an element by the scalar 1 gives back that element
  • 🎓 Understanding vector spaces will be useful for upcoming topics
Q & A

  • What is a vector space?

    -A vector space, also called a linear space, is a collection of elements that can be added together in any combination and multiplied by scalars in any combination. The elements must follow certain rules like commutative and associative properties of vector addition.

  • What is the closure property of a vector space?

    -The closure property states that for any element a in the vector space V, multiplying a by any scalar will result in an element that is also in V. Also, adding any two elements in V will result in an element that is also contained within V.

  • What does the set of real numbers R represent?

    -R represents the set of all real numbers, including positive, negative, rational, and irrational numbers.

  • Can a vector space contain more than just vectors?

    -Yes, a vector space can also contain matrices, functions, or other mathematical objects as long as the two closure properties are satisfied.

  • What was an example of a vector space made up of functions?

    -The set of linear polynomials in the form ax+b was given as an example. When multiplied by scalars or added together, linear polynomials remain linear polynomials, satisfying closure.

  • When are closure properties not satisfied?

    -Closure fails when multiplying or adding two elements in the set results in something outside of the original set. An example was a set of 2x1 vectors that always had 2 in the second row.

  • What does the notation Rn represent?

    -Rn represents the set of all real-valued vectors with length n, where n is some integer.

  • What does Rmxn represent?

    -Rmxn represents the set of all real-valued m x n matrices.

  • Why are matrices with the same dimensions a vector space?

    -Because multiplying matrices by scalars or adding matrices together does not change their dimensions, satisfying closure.

  • What topics involve working with vector spaces?

    -Many linear algebra and advanced calculus topics like bases, spanning, linear transformations, and function spaces rely heavily on the vector space concept.

Outlines
00:00
📝 Defining Vector Spaces and Closure Properties

This paragraph introduces the concept of a vector space V, which is a collection of elements that can be added together and multiplied by scalars. It states the properties vectors in V must follow, like commutative/associative addition and distribution of scalars. It then explains the closure property, which requires that multiplying an element by a scalar and adding two elements always results in something still contained in V.

05:01
👉 Examples of Vector Spaces

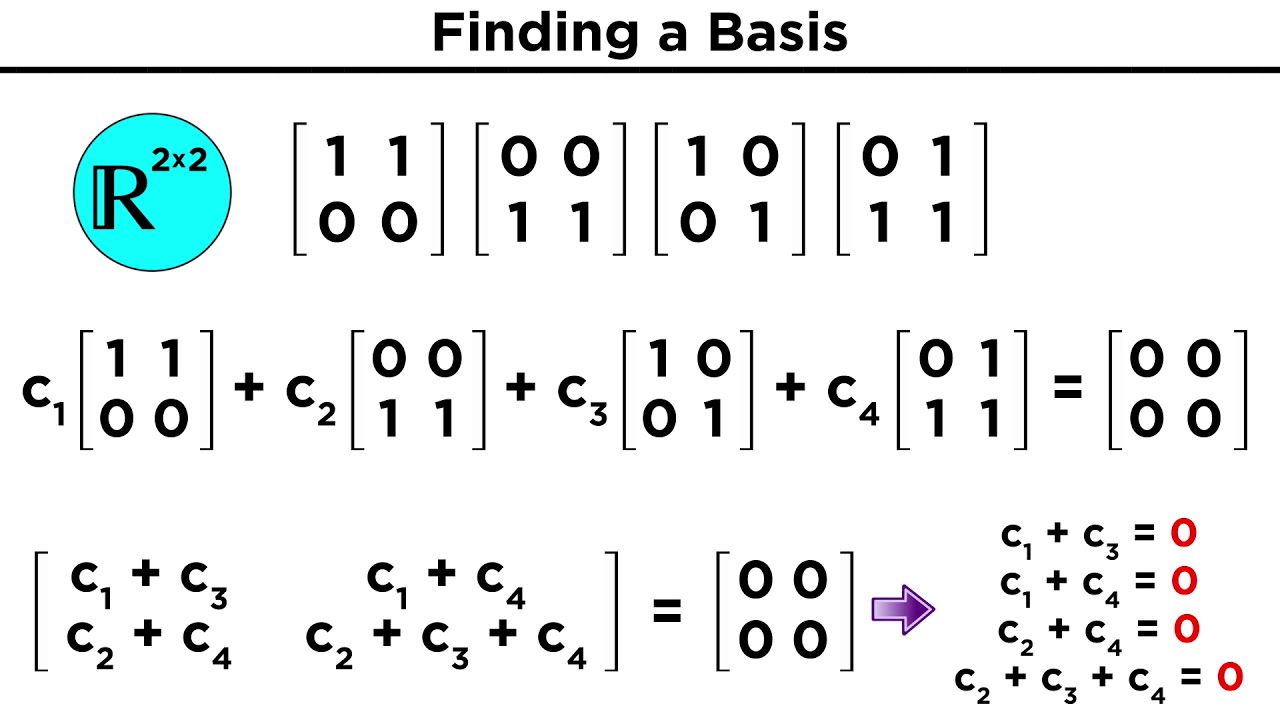
This paragraph provides examples of sets that satisfy the vector space properties, like the set of real numbers, the set of 3D vectors with real components, and the set of real matrices with fixed dimensions. It also gives an example of a vector space made of linear polynomial functions.

❌ Example of a Set Without Closure

This paragraph demonstrates a case where a set of 2D vectors does not form a vector space, because adding two elements results in a vector not contained in the original set due to a fixed second component. This violates the closure property.

Mindmap
Keywords
💡vector space
A vector space, also called a linear space, is a set of elements that can be added together and multiplied by scalars while satisfying certain properties. In the video, a vector space is denoted by V and its elements, such as vector A, are said to be members of V. The elements follow rules of vector addition and scalar multiplication. Importantly, a vector space must satisfy closure, meaning scalars multiplied by elements and sums of elements must result in outputs that are still members of the set V.
💡closure
Closure is a key property that a set must satisfy to be considered a vector space. There are two closure criteria: 1) Multiplying any element of the space by a scalar results in an output that is still an element of the space, and 2) Adding any two elements of the space results in a sum that is still an element of the space. The video shows how the set of real numbers and the set of 3-dimensional real vectors both satisfy closure and can be vector spaces.
💡real numbers
The set of all real numbers, denoted R, is shown to form a vector space. It includes positive and negative rational and irrational numbers. When any real number is multiplied by a scalar or two real numbers are added, the result is always another real number. So real numbers have closure and satisfy the vector space definition.
💡functions
The video demonstrates that even a set of functions can form a vector space. Specifically, the set of linear polynomial functions in the form ax+b is shown to be a vector space. Multiplying by scalars or adding two linear polynomials always outputs another valid linear polynomial.
💡matrices
For matrices of fixed dimensions, the set forms a vector space. Adding two matrices of the same dimensions or multiplying a matrix by a scalar cannot change its dimensions. So matrix sets of common dimensions satisfy closure and are vector spaces.
💡scalars
Scalars are numbers that vectors or other quantities can be multiplied by while retaining set membership or structure. Rules are shown for distributing scalars over vector sums or multiplying scalars together over a single vector. Scalars are key for defining vector spaces.
💡zero vector
The zero vector is a special element of a vector space that, when added to any other element, outputs that original element unchanged. This parallels the role of 0 for real numbers. The zero vector illustrates how vector addition has an inverse operation.
💡vector addition
As vectors are key components of vector spaces, rules of vector addition covered earlier still apply. These state vector sums are done component-wise and vector addition is commutative and associative.
💡vector length
While vector spaces can contain more than just vectors, the concept of vector length comes up for Rn vectors. Here, n denotes vectors of a fixed integer length that can multiply, add while maintaining that length to satisfy closure.
💡element
Elements or members are the components that make up a vector space, denoted V. The closure rules dictate that elements added or multiplied by scalars must remain in set V. Elements can be vectors, functions, etc.
Highlights

Researchers developed a new method to identify protein structures using cryogenic electron microscopy.

The new technique enabled determining protein structures at near atomic resolution, providing insights into their functions.

By flash freezing samples, the method overcame previous limitations in cryo-EM such as radiation damage and sample movement.

Researchers were able to visualize never before seen structural details critical to understanding protein mechanisms.

The findings could enable structure-based drug design and advance our understanding of disease pathways.

Combining cryo-EM with new computational analysis enabled 3D modeling of protein complexes in native states.

The research provides a new window into visualizing large, flexible, and transient protein assemblies at high resolutions.

By studying proteins in physiologically relevant environments, new insights can be gained into molecular interactions.

Technical innovations in microscope automation and direct electron detection were critical to the method's success.

The findings represent a major breakthrough in structural biology and hold promise for biomedical applications.

Challenges remain in applying the technique to smaller proteins and improving resolution limits.

Further development of computational tools will help analyze the vast complex datasets generated.

Overall the research demonstrates the power of cryo-EM for determining protein structures vital for biological understanding.

The new structural insights gained can guide protein engineering efforts and drug development.

This pioneering work opens the door to visualizing many previously hidden aspects of protein molecules in nature.

Transcripts

Browse More Related Video

Subspaces and Span

Linear Algebra: Introduction to Vectors

Basis and Dimension

Types of Matrices and Matrix Addition

Linear Independence

Linear combinations, span, and basis vectors | Chapter 2, Essence of linear algebra

Rate This

5.0 / 5 (0 votes)

Thanks for rating: