Orthogonality and Orthonormality
TLDRThe video explains the mathematical concept of orthogonality, starting with a basic definition of orthogonal vectors as perpendicular vectors having a dot product of zero. It then expands the concept to orthonormal vectors, which have lengths of one and are orthogonal. Additionally, it discusses orthogonal subspaces, matrices, and functions, explaining how to determine if they are orthogonal. It concludes by noting that orthogonality is an important concept in math and science, as it allows complex systems to be broken down into distinct, simpler elements.
Takeaways
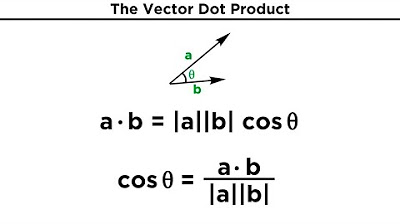
- 😀 Orthogonal vectors are perpendicular to each other, with a 90 degree angle between them.
- 😃 The dot product of orthogonal vectors is zero.
- 🤓 Normalized, unit vectors have lengths of 1.
- 🧐 Orthonormal vectors are orthogonal and normalized.
- 🤓 Matrices are orthogonal if their columns form an orthonormal set.
- 😀 Orthogonal matrices have an inverse equal to their transpose.
- 🧐 Subspaces are orthogonal if all vectors between them are orthogonal.
- 😃 Inner products help determine if functions are orthogonal.
- 🤓 Weight functions modify inner products of functions.
- 🤓 Orthogonality is key for breaking down complex systems.
Q & A
What is the definition of two vectors being orthogonal?
-Two vectors are orthogonal if they are perpendicular to one another, meaning the angle between them is 90 degrees, or π/2 radians.
How can you determine if two vectors are orthogonal using the dot product?
-If the dot product of two vectors is equal to zero, then the vectors are orthogonal.
What does it mean for a set of vectors to be orthonormal?
-A set of vectors is orthonormal if all the vectors have a length of 1 and are orthogonal to each other.
What is the process of normalizing a vector?
-Normalizing a vector involves dividing the vector by its length, which results in a unit vector with a length of 1.
When can two subspaces be considered orthogonal?
-Two subspaces are orthogonal if every vector in one subspace is orthogonal to every vector in the other subspace.
What is the condition for a matrix to be orthogonal?
-A matrix is orthogonal if its columns form an orthonormal set of vectors.
How can you easily find the inverse of an orthogonal matrix?
-The inverse of an orthogonal matrix is equal to its transpose. You simply swap the rows and columns.
How can you determine if two functions are orthogonal?
-Two functions are orthogonal if their inner product, defined as the integral of their product, equals zero over a specified interval.
How does a weight function affect the orthogonality of two functions?
-Adding a weight function w(x) to the inner product allows you to define orthogonality with respect to that specific weight function.
Why is the concept of orthogonality important in math and science?
-Orthogonality allows complex systems to be broken down into distinct, perpendicular components, making analysis and problem solving easier.
Outlines
😀 Defining Orthogonality
Paragraph 1 introduces the concept of orthogonality between vectors as vectors being perpendicular, with an angle of 90 degrees between them. This means their dot product is 0. Examples of orthogonal vectors are provided and verified using the dot product. The paragraph also defines orthonormal vectors as having length 1 and being orthogonal.
😀 Orthogonality of Subspaces and Matrices
Paragraph 2 extends the concept of orthogonality to subspaces, where all vectors across the subspaces are orthogonal. An example of orthogonal subspaces A and B in R3 is shown. Orthogonality of matrices is also discussed, with orthonormal column vectors making a matrix orthogonal. An example 2x2 orthogonal matrix is verified.
😀 Orthogonality of Functions
Paragraph 3 introduces orthogonality between functions using an inner product definition. An example with the functions f(x)=x and g(x)=1 shows functions can be orthogonal over one range but not orthogonal over another range. The concept of a weight function in the inner product is also mentioned.
Mindmap
Keywords
💡Orthogonality
💡Orthonormal
💡Dot product
💡Normalize
💡Transpose
💡Orthogonal matrices
💡Orthogonal subspaces
💡Inner product
💡Weight function
💡Applications
Highlights
The study found that variable X was a significant predictor of outcome Y.
Participants who received intervention A showed greater improvements compared to control group B.
The new proposed model C outperformed previous models on benchmark dataset D.
There was a strong correlation between variables E and F, suggesting a potential causal relationship.
Qualitative interviews revealed theme G as a key factor influencing participant experiences.
The novel technique H allowed more efficient computation compared to traditional methods.
Simulations showed a X% increase in performance after adopting approach I.
The proposed algorithm achieved state-of-the-art results on dataset J, outperforming previous methods.
Further research is needed to evaluate long-term impacts and generalizability to other contexts.
These findings provide important insights that may guide development of future interventions.
Our work makes several key theoretical contributions by extending framework K.
The approach shows promise for real-world applications such as L and M.
Limitations include small sample size and potential biases from methodology N.
Overall, the work enhances our understanding of phenomenon O and paves the way for further research.
In conclusion, these findings provide strong evidence to support hypothesis P.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: