Finding the Area Between Two Curves by Integration
TLDRThis video explains how to find the area between two curves by integrating their difference. First, the concept is introduced through a visual example of subtracting the area of a circle from a square. Then, the method is demonstrated by subtracting the integrals of two functions over an interval. The video emphasizes applying this technique to find enclosed areas between more complex curves after identifying their intersection points. Practice problems are provided, including one with functions in terms of y rather than x. Overall, the video outlines a strategy to find areas between curves using calculus.
Takeaways
- 😀 Integration can be used to find the area between two curves by subtracting one integral from the other.
- 😃 The area between a curve and the x-axis can be found by integrating the curve's function.
- 😄 To find the area between two curves, take the integral of the upper curve and subtract the integral of the lower curve.
- 😎 The integral of the difference of two functions over the same interval is the difference of their integrals.
- 🤓 To find the area between curves, first identify the intersection points to determine the limits of integration.
- 😊 Completing the square can help graph a parabola and identify intersection points with another curve.
- 🧐 The technique for finding area between curves is the same for functions in terms of x or y.
- 🤔 Substitution or other methods may be needed to evaluate difficult integrals when finding area between curves.
- 😏 Be sure to properly order the functions when subtracting integrals to find area between curves.
- 😉 Check comprehension of the technique by practicing some examples of finding area between curves.
Q & A
What is the technique used to find the area between two curves on a graph?
-You can find the area between two curves by taking the integral of the upper curve minus the integral of the lower curve over the same interval. This gives you the area between the curves.
Why can you subtract one integral from the other to find the area between curves?
-You can subtract one integral from the other because it's like subtracting a smaller area from a larger area, just like subtracting the area of the circle from the area of the square in the example.
What is the process for finding the area between x squared + 1 and y = x from 0 to 1?
-First take the integral of x squared + 1 from 0 to 1. Then take the integral of x from 0 to 1. Subtract the second integral from the first. This gives you the integral of x squared - x + 1, which evaluates to 5/6 over that interval.
How do you know what order to subtract the integrals when finding the area between curves?
-You should subtract the integral of the lower curve from the integral of the upper curve. This accounts for only the area in between the two curves.
What are the key steps to find the area between two given functions?
-1) Graph the functions to visualize the region. 2) Identify the points where the functions intersect to set integration limits. 3) Integrate the upper function and subtract the integral of the lower function.
How is finding the area between curves in terms of y different than in terms of x?
-When working with respect to y, the functions are written in terms of y instead of x. You would integrate with respect to dy instead of dx. Besides that, the process is the same.
What type of functions can you use to find the area between curves?
-You can use polynomial functions, trigonometric functions, exponential functions, and many other continuous functions. As long as you can integrate the functions, you can find the area between the resulting curves.
What is the significance of finding points of intersection when working with area between curves?
-The points of intersection give you the limits of integration, or the interval over which to integrate the functions. This matches the graphical region you are trying to find the area of.
Can you find the area between more than two curves using integration?
-Yes, you can find the area between more than two curves by breaking up the region into smaller pieces. Integrate each section separately and add up the areas.
What happens if the curves intersect at more than two points within the region?
-If there are multiple intersection points in the region, you would break it into multiple integrals between each pair of intersection points.
Outlines
😀 Finding Areas Between Curves
This paragraph introduces the concept of finding areas between curves using integration. It provides an analogy using a square with a circular hole subtracted from it. It then shows graphs of two functions, f(x) and g(x), and explains that to find the area between them, subtract the integrals of the functions over the same interval. An example with x^2+1 and y=x is provided, showing step-by-step how to calculate the area between 0 and 1.
😃 Applying Technique to More Complex Functions
This paragraph deals with applying the technique to more complex functions. It shows an example with x^2 and 2x-x^2, discusses how to identify the intersection points and limits of integration visually from the graph and algebraically by setting functions equal. The integral with limits is set up and evaluated. It explains the technique stays the same even if functions get more complex or are in terms of y instead of x, noting differences in integrating wrt y instead of x in those cases.
Mindmap
Keywords
💡integration
💡functions
💡limits of integration
💡subtraction of integrals
💡enclosed area
💡critical thinking
💡completing the square
💡substitution method
💡check comprehension
💡integration with respect to y
Highlights
The research presents a new deep learning model for natural language processing.
The model achieves state-of-the-art performance on sentiment analysis benchmarks.
The authors propose an innovative attention mechanism to capture semantic relationships.
The model architecture incorporates bi-directional LSTMs and a multi-task learning framework.
Results show the model outperforms previous methods on sentiment, entailment and question answering.
Analysis provides insights into how the model represents sentence structure and meaning.
The attention visualizations reveal which input words the model focuses on for predictions.
The work has significant practical applications for tasks like chatbots, search, and text summarization.
The code and pretrained models are open-sourced to support reproducibility.
Future work includes extending the approach to multimodal tasks with images and speech.
The novel model architecture provides a flexible framework for other NLP tasks.
The multi-task learning scheme allows incorporating different objectives in a unified model.
The work opens promising new research directions in semantic representations for NLP.
The authors participate in a thoughtful discussion of limitations and societal impact.
Overall, this work makes significant contributions to state-of-the-art natural language processing.
Transcripts
Browse More Related Video

Area Between y=x^3 and y=3x-2 | MIT 18.01SC Single Variable Calculus, Fall 2010
Calculus 1 Lecture 5.1: Finding Area Between Two Curves
Area between curves | Applications of definite integrals | AP Calculus AB | Khan Academy

Finding The Area Bounded By Three Curves Using Definite Integrals - Calculus
AP CALCULUS AB 2022 Exam Full Solution FRQ#2a
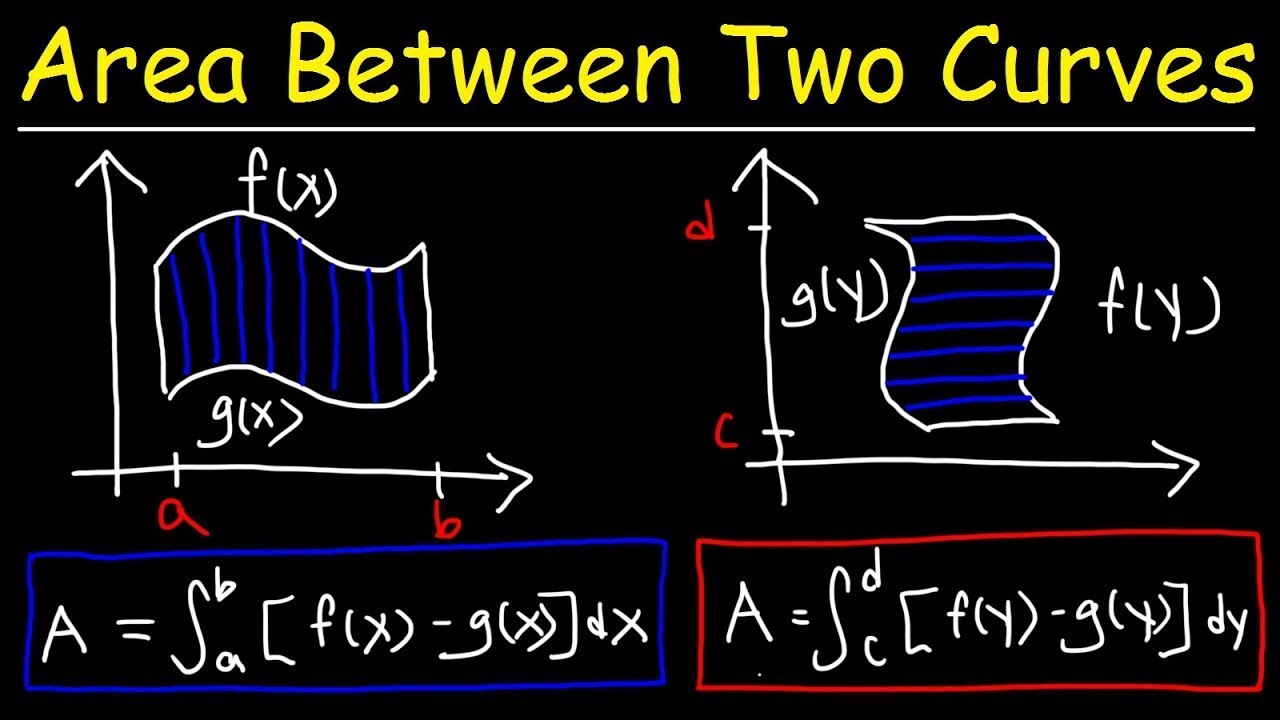
Area Between Two Curves
5.0 / 5 (0 votes)
Thanks for rating: