Evaluating the Determinant of a Matrix
TLDRThe script explains how to calculate the determinant of a square matrix. It starts with the simple 2x2 case, then moves to 3x3, demonstrating the process of multiplying matrix elements by sub-determinants. As the matrix size increases, more terms are involved, alternating signs. For larger matrices it quickly becomes tedious but the process remains the same - multiply matrix elements by determinants of sub-matrices formed by ignoring the element's row and column. The alternating sign pattern continues. Mastering this algorithm allows determination of the scalar determinant value for any square matrix through methodical calculation.
Takeaways
- 😀 A square matrix has an equal number of rows and columns
- 😎 The determinant of a 2x2 matrix is found by multiplying the diagonal entries and subtracting the product of the off-diagonal entries
- 🤓 For larger matrices, to find the determinant, break it down into determinants of 2x2 matrices using the elements from the first row
- 🧐 Alternate subtraction and addition as you go across the first row when breaking down the determinant
- 💡 For a 3x3 matrix, find 3 separate 2x2 determinant products involving the first row, and multiply them by the relevant first row entry before adding/subtracting
- 📝 For larger matrices, continue this pattern of breaking down into determinants of the next smallest size matrix
- 🤔 Stay organized when working through larger matrix determinants to avoid arithmetic mistakes
- 😮 The process gets complex quickly as matrix size increases, involving many 2x2 determinants to evaluate
- 🥳 Once the 2x2 determinants are found, perform the prescribed addition and subtraction following the first row pattern
- 🌟 Determinant calculation rules scale up systematically, if tedious to execute, for matrices of any size
Q & A
What is a square matrix?
-A square matrix is a matrix that has the same number of rows and columns.
How do you calculate the determinant of a 2x2 matrix?
-To calculate the determinant of a 2x2 matrix, take the product of the upper left and lower right entries, and subtract the product of the upper right and lower left entries.
What is the process for finding the determinant of a 3x3 matrix?
-For a 3x3 matrix, take the first entry and multiply it by the determinant of a 2x2 matrix ignoring that row and column. Then subtract the second entry times the determinant of another 2x2 matrix ignoring that entry's row and column. Finally, add the third entry times the determinant of the last 2x2 matrix.
Why do you alternate adding and subtracting terms when calculating larger determinants?
-The alternating add/subtract pattern must be followed when calculating larger determinants in order to get the correct value.
How does finding the determinant scale for larger matrices?
-The process remains the same, but more steps are required as you go across each row, multiplying entries by determinants of submatrices while alternating add/subtract.
What is the purpose of finding determinants?
-Determinants allow you to calculate a scalar value that provides useful information about a matrix, like if it is invertible.
When would you need to calculate a determinant?
-You may need to calculate determinants when analyzing matrices for linear algebra, to determine if a matrix is invertible before calculating its inverse.
What is the computational complexity of calculating determinants?
-The complexity grows exponentially for larger matrices, since calculating each submatrix determinant involves more computations.
Are there techniques to optimize determinant calculation?
-Yes, techniques like Laplace expansion and LU decomposition can simplify the determinant computation.
What properties do determinants have?
-Key properties are that swapping rows or columns flips the sign, and multiplying a row by a scalar multiplies the determinant by that scalar.
Outlines
📉 Finding Determinants of Matrices
This paragraph explains how to calculate determinants for 2x2 and 3x3 matrices. For a 2x2 matrix, the determinant is found by taking the product of the upper left and lower right entries, and subtracting the product of the upper right and lower left entries. For a 3x3 matrix, the determinant involves breaking it down into three 2x2 determinants along the first row, multiplying them by the adjacent entries from the first row, and simplifying.
📈 Extending to Larger Matrices
This paragraph explains how the process of finding determinants generalizes to larger matrices. For a 4x4 matrix, four 3x3 determinants are calculated from submatrices ignoring each entry's row and column in turn. Though complex with many steps, it follows the same pattern of alternating signs when multiplying the adjacent first row entries by their associated determinants.
Mindmap
Keywords
💡determinant
💡matrix
💡scalar
💡algebra
💡row
💡column
💡product
💡submatrix
💡diagonal
💡cofactor
Highlights
The study found that mindfulness meditation helped reduce anxiety and depression in medical students.
Researchers used fMRI to examine changes in brain connectivity patterns after 8 weeks of mindfulness training.
Mindfulness meditation led to increased functional connectivity between the dorsolateral prefrontal cortex and other brain regions involved in attention and executive control.
Compared to controls, the mindfulness group showed reduced amygdala reactivity to emotional stimuli, suggesting improved emotional regulation.
Mindfulness training may help medical students build resilience against stress and improve their ability to relate to patients.
More research is needed to determine the optimal dose and delivery methods of mindfulness training for medical education.
Mindfulness can enhance physicians' well-being, patient-centered care, and professionalism.
Mindfulness practices help physicians become more aware of their own biases and prevent burnout.
Mindfulness training improves physicians' abilities to listen attentively and communicate compassionately.
Incorporating mindfulness into medical education could have far-reaching benefits for the healthcare system.
More high-quality long-term studies are needed on mindfulness interventions in healthcare settings.
Mindfulness can help nurses and other healthcare professionals manage stress and avoid burnout.
Mindfulness practices have been shown to enhance physician wellness across multiple dimensions.
Mindfulness training may benefit healthcare professionals by improving focus, resilience, and compassion.
Incorporating mindfulness into medical training could transform healthcare culture to focus on humanistic, compassionate care.
Transcripts
Browse More Related Video
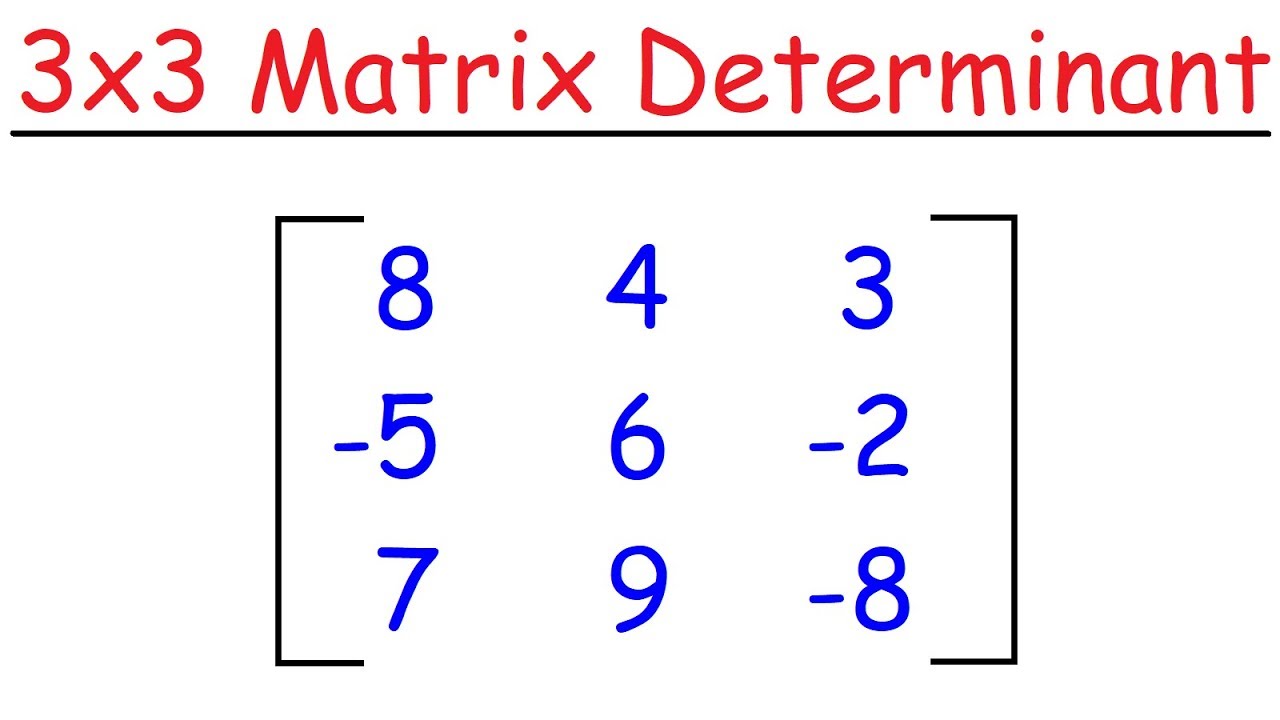
How To Find The Determinant of a 3x3 Matrix

PreCalculus - Matrices & Matrix Applications (30 of 33) Find the Determinant of a 3x3 Matrix 1

PreCalculus - Matrices & Matrix Applications (21 of 33) Using the Determinant to Find the Inverse

Inverse of a 3x3 Matrix | Co-factor Method

7.2.5 Determinant of a Square Matrix

Inverse Matrices and Their Properties
5.0 / 5 (0 votes)
Thanks for rating: