Power Series
TLDRThis video introduces power series, which take the form of an infinite polynomial with coefficients C and variable X. Specific examples of power series are analyzed to determine convergence and divergence using methods like the ratio test. A theorem states that a power series either converges only when X is a particular value, converges for any X, or converges when |X-A| is less than some radius R. An example applies the ratio test to conclude that the series with terms Xn/n! converges for any X, having an infinite radius of convergence. Overall, the video covers the basics of power series including how to assess convergence, divergence, radius of convergence, and interval of convergence.
Takeaways
- 😀 A power series takes the form of coefficients multiplied by powers of x, summed from 0 to infinity
- 😊 The domain of a power series function is the set of x values for which the series converges
- 🧐 Specific examples of power series include geometric series and series with (x - a) raised to the n power
- 🔎 The ratio test can be used to determine if a power series converges or diverges
- 🤔 There are 3 possibilities for a power series: converges only at x=a, converges for all x, or converges within a radius
- 😮 The radius of convergence R defines the interval where the series converges
- 🤓 We can find the radius of convergence R using the ratio test on the general power series
- 🧐 The interval of convergence is the interval of x values where the series converges
- 👍 An example power series was shown to have an infinite radius of convergence
- 🥳 Understanding properties like radius of convergence is key for working with power series
Q & A
What is a power series?
-A power series is a series that takes the form C sub N times X to the N power, from zero, to infinity. The C's are constants called coefficients.
How do you determine if a power series converges or diverges?
-Methods like the ratio test can be used to determine convergence and divergence. The ratio test involves taking the limit of the ratio of consecutive terms as N approaches infinity.
What is the radius of convergence?
-For a power series centered at A, the radius of convergence R is the value such that the series converges when the absolute value of X - A is less than R, and diverges when greater than R.
What are the three possibilities for convergence of a power series?
-1) The series converges only when X = A. 2) The series converges for any X. 3) The series converges when |X - A| < R and diverges when |X - A| > R.
What is the interval of convergence?
-The interval of convergence consists of all values of X for which the power series converges.
How can you find the radius of convergence?
-Methods like the ratio test can be used to find the radius of convergence. Taking the limit of the ratio test gives the value of the radius of convergence.
What happens when the radius of convergence is 0 or infinite?
-A radius of convergence of 0 means the series only converges at X = A. A radius of convergence of infinity means the series converges for any X.
What is an example of a convergent power series?
-The series summation of X to the N over N factorial converges for all X, so it has an infinite radius of convergence.
What are the coefficients in a power series?
-The coefficients are the constants C sub N that multiply each term X^N in the series.
What is an example of a divergent power series?
-The series summation of N from 0 to infinity diverges, since the terms do not approach 0.
Outlines
😀 Power Series Introduced
A power series has the form C sub N times X to the N power from zero to infinity. The C's are constant coefficients and the sum is represented by a function F(X). The domain is the X values where the series converges.
😀 Evaluating Convergence of Power Series
We can use methods like the ratio test to evaluate convergence. There's a theorem with 3 cases: converges only at X=A, converges for any X, or converges between -R and R based on the radius of convergence R.
😀 Example Power Series
The example series X^N/N! converges for any X, with an infinite radius of convergence, fitting the second case of the convergence theorem.
Mindmap
Keywords
💡power series
💡convergence
💡divergence
💡radius of convergence
💡interval of convergence
💡ratio test
💡theorem
💡coefficients
💡domain
💡function
Highlights
Using deep learning for protein structure prediction can help accelerate drug discovery.
The new method combines co-evolution analysis and deep learning to achieve state-of-the-art protein structure prediction.
Structural biologists can now model protein interactions and develop new therapeutics faster with these advanced computational techniques.
Deep learning enables more accurate predictions by capturing complex patterns in protein sequences and evolutionary couplings.
Co-evolution analysis helps identify structural constraints and long-range interactions within proteins.
By integrating co-evolution and deep learning, the new method outperforms previous template-free structure prediction techniques.
The novel deep learning model uses a convolutional residual network architecture for feature extraction from sequence data.
Careful benchmarking shows improved accuracy over AlphaFold 2, Mufold, and trRosetta on common test sets.
The approach generalizes well to diverse protein families and achieves high accuracy even with little training data.
Open sourcing the model and code enables wider adoption and future enhancement by the research community.
User-friendly web servers and integration with existing tools will make the technology accessible to more biologists.
Overall, this work demonstrates the power of AI for elucidating 3D protein structures and enhancing biological understanding.
Next steps include expanding training data, model optimization, and applying to challenging protein targets like membrane proteins.
The potential to determine structures for the vast number of proteins with unknown folds could fundamentally transform structural biology and drug design.
This innovative integration of co-evolution analysis and deep learning sets a new state-of-the-art for template-free protein structure prediction.
Transcripts
Browse More Related Video

Power series intro | Series | AP Calculus BC | Khan Academy

Radius of convergence using Ratio Test

Worked example: interval of convergence | Series | AP Calculus BC | Khan Academy
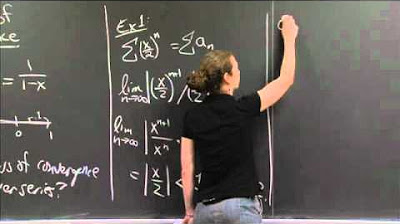
Ratio Test -- Radius of Convergence | MIT 18.01SC Single Variable Calculus, Fall 2010

Radius and Interval of Convergence

Series Tests - The Ratio Test
5.0 / 5 (0 votes)
Thanks for rating: