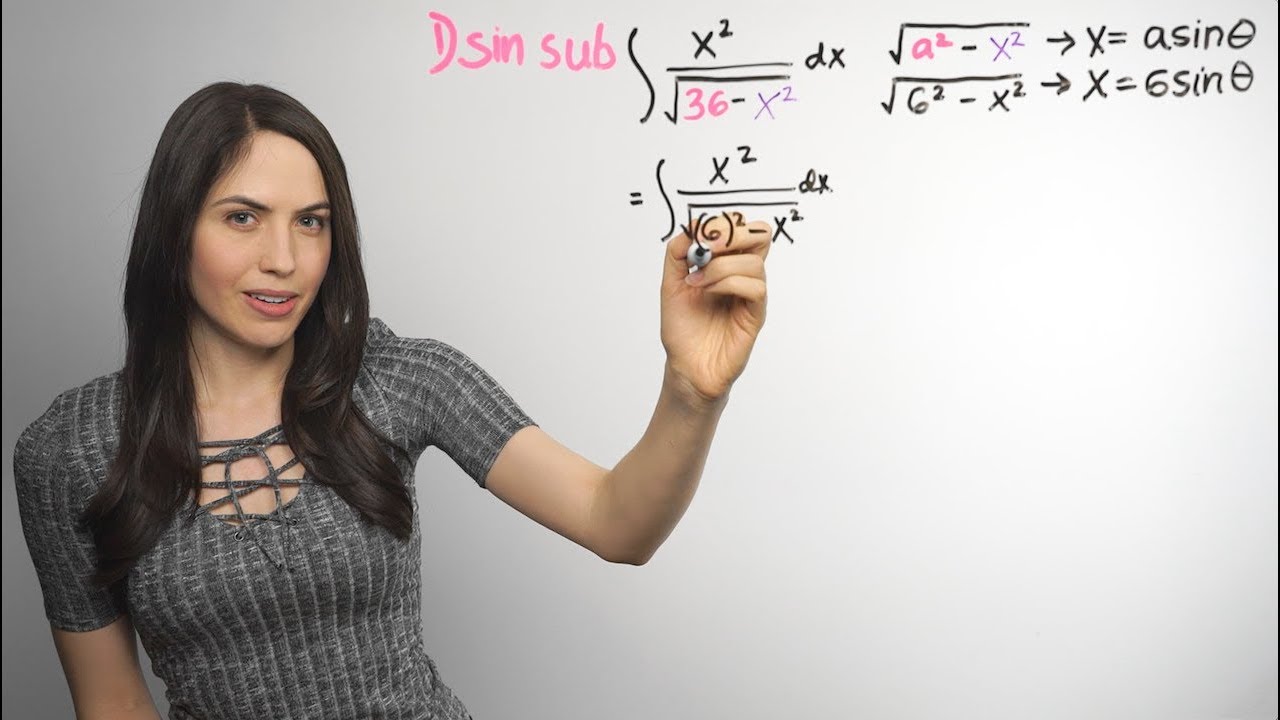Integration By Trigonometric Substitution
TLDRThe script discusses integration by trigonometric substitution, a technique for integrals containing one of three specific radical expressions. It explains how making trigonometric substitutions for x simplifies these expressions via Pythagorean identities. An example shows the process: make the substitution, convert dx into dθ, integrate with respect to θ, then convert θ back to x using a labeled triangle. Two more examples demonstrate applying the technique. The video teaches three key integration tricks - substitution rule, integration by parts, and now trigonometric substitution - and notes that determining which to apply takes practice.
Takeaways
- 📚 Trigonometric substitution is a technique for integrating expressions containing √(A² - x²), √(A² + x²), or √(x² - A²), where A is any positive number.
- 📈 It differs from the substitution rule and integration by parts, filling a gap when these methods are not applicable due to the absence of a suitable du term.
- 🤖 Specific substitutions are required: x = A sin(θ) for √(A² - x²), x = A tan(θ) for √(A² + x²), and x = A sec(θ) for √(x² - A²).
- ✅ These substitutions simplify the integrand by leveraging Pythagorean identities, transforming the radical expressions into simpler trigonometric functions.
- ⏱️ Converting dx to dθ is crucial, requiring differentiation of the substitution expression to proceed with integration in terms of θ.
- 🔬 The technique involves three key steps: identifying the specific radical expression, performing the trigonometric substitution and simplification, and integrating the resulting expression.
- 🌐 After integration, results in terms of θ are converted back to x using trigonometric identities and the geometry of a right-angled triangle.
- ✔️ This method is particularly useful for integrands that are not directly integrable using standard techniques, enabling integration of complex radical expressions.
- 📝 Practice and familiarity with trigonometric identities and substitutions are essential for effectively applying trigonometric substitution.
- 👀 The choice between substitution, integration by parts, and trigonometric substitution depends on the form of the integrand, highlighting the importance of strategy in integration.
Q & A
What are the three specific terms that allow trigonometric substitution to be used?
-The three specific terms are: the square root of A squared minus x squared, the square root of A squared plus x squared, and the square root of x squared minus A squared.
What is the substitution that must be made when the term 'square root of A squared minus x squared' is present?
-When the term 'square root of A squared minus x squared' is present, x must be substituted with A sine theta.
Why must dx be changed to dtheta after making the trigonometric substitution?
-Dx must be changed to dtheta because the substitution changes everything to be in terms of theta. To integrate with respect to theta, there must be a dtheta term rather than dx.
What are the three main steps when using trigonometric substitution?
-The three main steps are: 1) Recognize which of the three expressions allows substitution and make the appropriate substitution. 2) Manipulate dx to get an expression with dtheta. 3) Construct a triangle to change the integral back into terms of x after integrating with respect to theta.
When can the substitution rule be used vs when can trig substitution be used?
-The substitution rule can be used when the integrand has a term that can act as du. Trig substitution is used when one of the three specific radical terms is present and the substitution rule does not apply.
What does the procedure look like to change the integral solution back to terms of x?
-A triangle is constructed using the original substitution. The triangle is labeled so that terms with theta can be converted back into terms with x using trigonometric ratios.
What is cotangent squared theta equal to in terms of more basic trig functions?
-Cotangent squared theta is equal to cosecant squared theta minus one.
Why convert cotangent theta to an expression involving x in the first example?
-The original integral was in terms of x, so the final solution needs to be as well. Converting cotangent theta allows the solution to be written with the original variable x rather than theta.
What additional method had to be used to evaluate the integral in the second example?
-After the trig substitution, another substitution of u=sine theta was required. This allowed the integral to be evaluated using basic substitution methods.
Why are three substitution techniques useful to know?
-Having multiple integration techniques available allows for determining the best approach based on the form of the integrand. Each technique handles certain forms particularly well.
Outlines
📝 Introducing Trigonometric Substitution
Paragraph 1 introduces trigonometric substitution, a technique for integrating certain functions containing radicals. It explains that trigonometric substitution works when the integrand contains one of three specific terms - the square root of A^2 - x^2, A^2 + x^2, or x^2 - A^2. For each of these three cases, a specific trigonometric substitution must be made - x = A sinθ, x = A tanθ, or x = A secθ.
😊 Walkthrough of Trig Substitution Example
Paragraph 2 walks through a specific example of using trigonometric substitution to integrate √(9 - x^2) / x^2 dx. It substitutes x = 3sinθ, converts dx to dθ, simplifies the integrand, performs the integration, and converts the final result back in terms of x.
👍 Another Trig Substitution Example
Paragraph 3 provides another example of applying trigonometric substitution to integrate 1 / [x^2 * √(x^2 + 4)] dx. It substitutes x = 2tanθ, simplifies, integrates, and converts back to x. This illustrates the full process again.
Mindmap
Keywords
💡integration
💡substitution rule
💡integration by parts
💡trigonometric substitution
💡Pythagorean identities
💡hypotenuse
💡integrand
💡adjacent
💡opposite
💡comprehension
Highlights
First significant research finding
Introduction of innovative methodology
Key conclusion with practical applications
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: