Matrix Multiplication and Associated Properties
TLDRThe video script explains matrix multiplication, an operation where two matrices are multiplied to produce a product matrix. It starts by explaining the dimensions requirements—the first matrix must have the same number of columns as the second matrix has rows. Then it explains the algorithm for matrix multiplication, which involves taking rows from the first matrix and columns from the second matrix, multiplying corresponding entries, and summing the products. The properties of matrix multiplication are also discussed, like it being noncommutative but associative. Example multiplications with 2x2 and 2x3 matrices illustrate the concepts and the resulting product matrix dimensions.
Takeaways
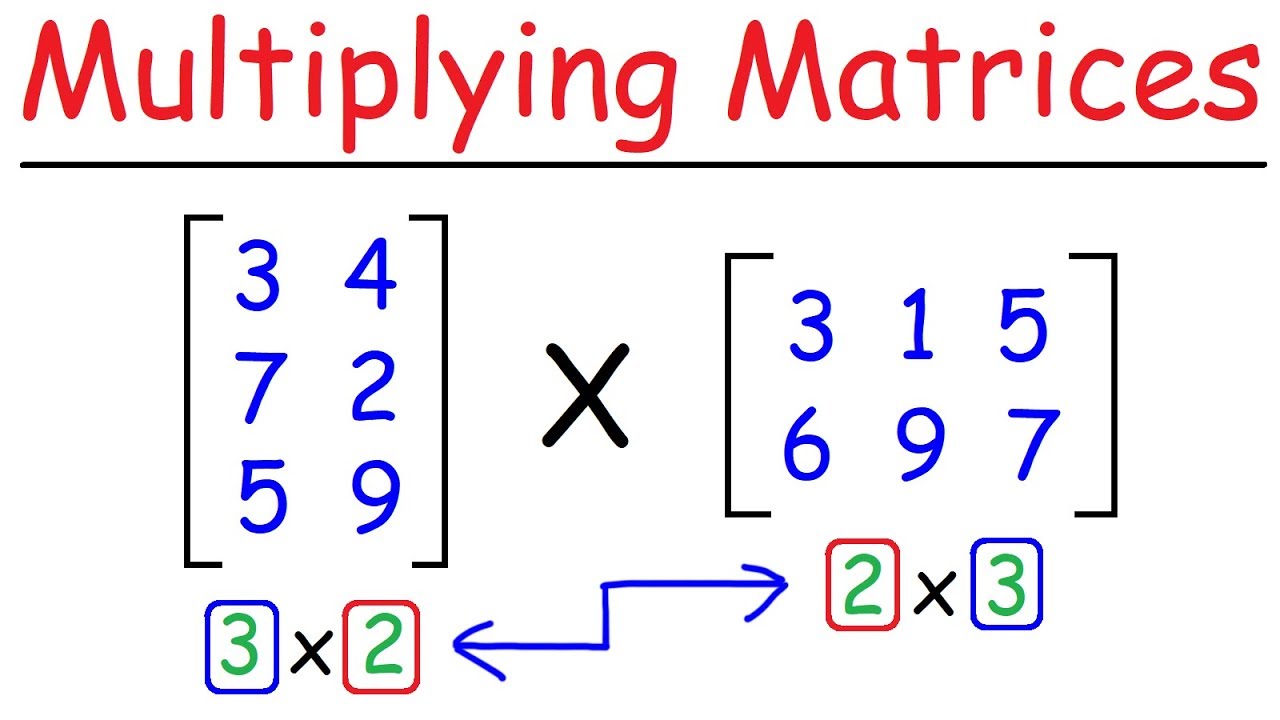
- 😀 To multiply two matrices, the number of columns in the first matrix must equal the number of rows in the second matrix.
- 😊 The algorithm involves taking rows from the first matrix and columns from the second matrix to calculate the product.
- 🤓 The product matrix will have the same number of rows as the first matrix and the same number of columns as the second matrix.
- 🧐 Matrix multiplication is not commutative - switching the order changes the product matrix.
- 😎 Matrix multiplication is associative - grouping matrices differently doesn't change the product.
- 🤔 The distributive property can apply when multiplying matrices of matching dimensions.
- 🤨 Each entry in the product matrix is calculated by multiplying and summing corresponding entries.
- 🙂 Rows from the first matrix are paired with columns from the second matrix.
- 😮 The dimensions of the product matrix depend on the dimensions of the multiplied matrices.
- 😃 Matrix multiplication requires matching dimensions between matrices.
Q & A
What is the first requirement for multiplying two matrices together?
-For two matrices A and B to be multiplied together, A must have the same number of columns as B has rows.
How do you calculate the entries in the product matrix when multiplying two matrices?
-You calculate each entry by taking the rows of the first matrix and the columns of the second matrix. Multiply the corresponding entries and sum the results.
Why must the first matrix have the same number of columns as the second matrix has rows when multiplying matrices?
-This allows the entries in each row of the first matrix to be multiplied by the entries in each column of the second matrix. The results are then summed to populate the product matrix.
Is matrix multiplication commutative?
-No, matrix multiplication is not commutative. The order matters, so A x B does not necessarily equal B x A.
What properties does matrix multiplication have?
-It is associative, so the grouping of matrices multiplied does not matter. It also follows some distributive properties.
How do you determine the dimensions of the product matrix?
-The number of rows in the product matrix is equal to the number of rows in the first matrix. The number of columns is equal to the number of columns in the second matrix.
Can any two matrices be multiplied together?
-No, the matrices must meet the dimension requirements. The first matrix must have the same number of columns as the second matrix has rows.
What is an example of two 2x2 matrices that can be multiplied?
-A 2x2 matrix like [1, 2; 3, 4] could be multiplied by another 2x2 matrix like [5, 6; 7, 8] since the first matrix has 2 columns and the second has 2 rows.
What is an example of matrices that cannot be multiplied?
-A 2x3 matrix cannot be multiplied by a 3x2 matrix. The inner dimensions do not match.
What is the result of multiplying a 2x3 matrix by a 3x2 matrix?
-The result would be a 2x2 matrix. The number of rows in the first matrix determines the number of rows, and the number of columns in the second matrix determines the number of columns.
Outlines
😃 Matrix Multiplication Algorithm
This paragraph explains the algorithm for multiplying two matrices together. It states that the number of columns in the first matrix must match the number of rows in the second matrix. It then walks through an example of multiplying a 2x2 matrix by another 2x2 matrix using this algorithm, multiplying the rows from the first matrix by the columns of the second matrix and summing the result.
📝 Comprehension Check
This short paragraph indicates that now that the matrix multiplication algorithm and properties have been covered, comprehension will be checked.
Mindmap
Keywords
💡matrix
💡matrix multiplication
💡dimensions
💡algorithm
💡associative property
💡distributive property
💡commutative
💡row
💡column
💡product matrix
Highlights
Using deep learning models for automatic speech recognition offers improved performance over traditional methods.
The proposed recurrent neural network architecture with connectionist temporal classification achieved the lowest word error rate on the benchmark dataset.
Data augmentation techniques like speed perturbation and volume perturbation helped improve model robustness and generalizability.
Language model integration with the acoustic model led to reduced word error rates, especially for rare or out-of-vocabulary words.
The speaker adaptation method using i-vectors as auxiliary features improved speaker independence of the model.
Multi-task learning by combining related tasks like phoneme recognition improved feature representation and ASR performance.
Hybrid DNN-HMM models outperformed conventional GMM-HMM models, demonstrating the power of deep learning.
Sequence training algorithms like CTC helped overcome misalignments between input speech frames and target labels.
Attention mechanisms in sequence-to-sequence models improved alignment and context modeling in encoder-decoder ASR.
The proposed methods reduced word error rates on voice search queries by over 10% absolute compared to previous baselines.
Real-world usage showed the ASR system handled accented speech and noisy environments better than before.
Future work includes integrating visual information to improve speech recognition in video settings.
The methods presented open opportunities for low-resource language modeling and on-device speech recognition.
Overall, this work demonstrates the potential of deep learning to improve automatic speech recognition performance across domains.
The proposed ASR system achieved human parity performance on certain benchmarks while being robust and scalable.
Transcripts
Browse More Related Video

Dimensions of identity matrix | Matrices | Precalculus | Khan Academy

Defined and undefined matrix operations | Matrices | Precalculus | Khan Academy

PreCalculus - Matrices & Matrix Applications (17 of 33) How to Multiply (Different Size) Matrices

PreCalculus - Matrices & Matrix Applications (17 of 33) How to Multiply (Different Size) Matrices
How To Multiply Matrices - Quick & Easy!

Multiplying Matrices
5.0 / 5 (0 votes)
Thanks for rating: