Estimating Sums Using the Integral Test and Comparison Test

Professor Dave Explains
22 Jun 201809:56
EducationalLearning
32 Likes 10 Comments

TLDRThe script discusses mathematical techniques for determining if infinite series converge or diverge. It introduces the integral test, explaining how to estimate series sums by calculating related improper integrals. It also covers the comparison test, allowing assessment of convergence by comparing a series to a known convergent or divergent series. Key points include how to apply these tests and how they help determine convergence and provide bounds on infinite series sums.

Takeaways
  • 😀 The integral test is a useful trick to estimate the sum of a convergent series
  • 👍 Using the integral test: a) Plot the terms of the series as a function f(x). b) The sum is roughly the area above f(x)
  • 🔎 P-series are series with terms of the form 1/n^p. They converge if p > 1, diverge if p ≤ 1.
  • 📖 The comparison test compares a series to one known to converge/diverge. If terms are smaller (larger), the series must also converge (diverge)
  • 🔍 The integral test: if f(x) is positive, continuous, decreasing to 0 and ∫ f(x) converges, then ∑ f(n) converges
  • 🧮 Compare a series to one you know converges/diverges. If terms are smaller/larger it must also converge/diverge.
  • 😵 Divergent series go to infinity. Convergent series have a finite sum as upper bound
  • 😊 The integral test estimates series sums by calculating areas under plots of terms
  • 😉 P-series converge if the power is > 1, diverge if power ≤ 1
  • 📝 The comparison test compares series term-by-term to deduce convergence/divergence
Q & A

  • What is the integral test and how can it be used?

    -The integral test is a technique to estimate the sum of a convergent series. It involves creating a continuous function from the terms of the series, calculating the improper integral of that function, and using it to approximate the sum.

  • When can the integral test be applied to a series?

    -The integral test can be applied when there is a decreasing, positive, continuous function F(x) defined on the interval [1, ∞) such that the Nth term of the series is given by F(N).

  • What is a p-series and what does the integral test tell us about p-series?

    -A p-series is a series of the form 1/N^p. The integral test shows that a p-series converges if p > 1 and diverges if p ≤ 1.

  • What is the comparison test?

    -The comparison test is used to determine convergence or divergence of a series by comparing it term-by-term to another series whose behavior is known. If the n-th term of one series is smaller than the n-th term of a convergent series, the first series is also convergent.

  • What are the conditions for using the comparison test?

    -If each term of series A is less than or equal to the corresponding term of a convergent series B, then A is also convergent. If each term of A is greater than or equal to the corresponding term of a divergent series B, then A is also divergent.

  • How do you assess convergence of the series 1/(2^N + 1)?

    -Compare it to the convergent geometric series 1/2^N. Since each term of 1/(2^N + 1) is less than the corresponding term of 1/2^N, the series 1/(2^N + 1) is also convergent by the comparison test.

  • How would you summarize the key points about convergent series?

    -The key points are: use tests like the integral test and comparison test to assess convergence; p-series converge for exponents > 1; techniques like integrals can estimate convergent series sums.

  • What does it mean for a series to converge?

    -A series converges if the sequence of partial sums has a finite limit. This means the terms get small enough that adding more terms does not change the sum significantly.

  • What is an example of a divergent series?

    -An example is the harmonic series: 1 + 1/2 + 1/3 + ... As more terms are added, the sum continues growing without bound, so the sequence of partial sums does not converge to a finite number.

  • How are series and sequences related?

    -A series is a sequence of partial sums formed by adding the successive terms of another sequence. The convergence of the series depends on the behavior of this sequence of terms.

Outlines
00:00
😁 Introduction to Convergent Series and the Integral Test

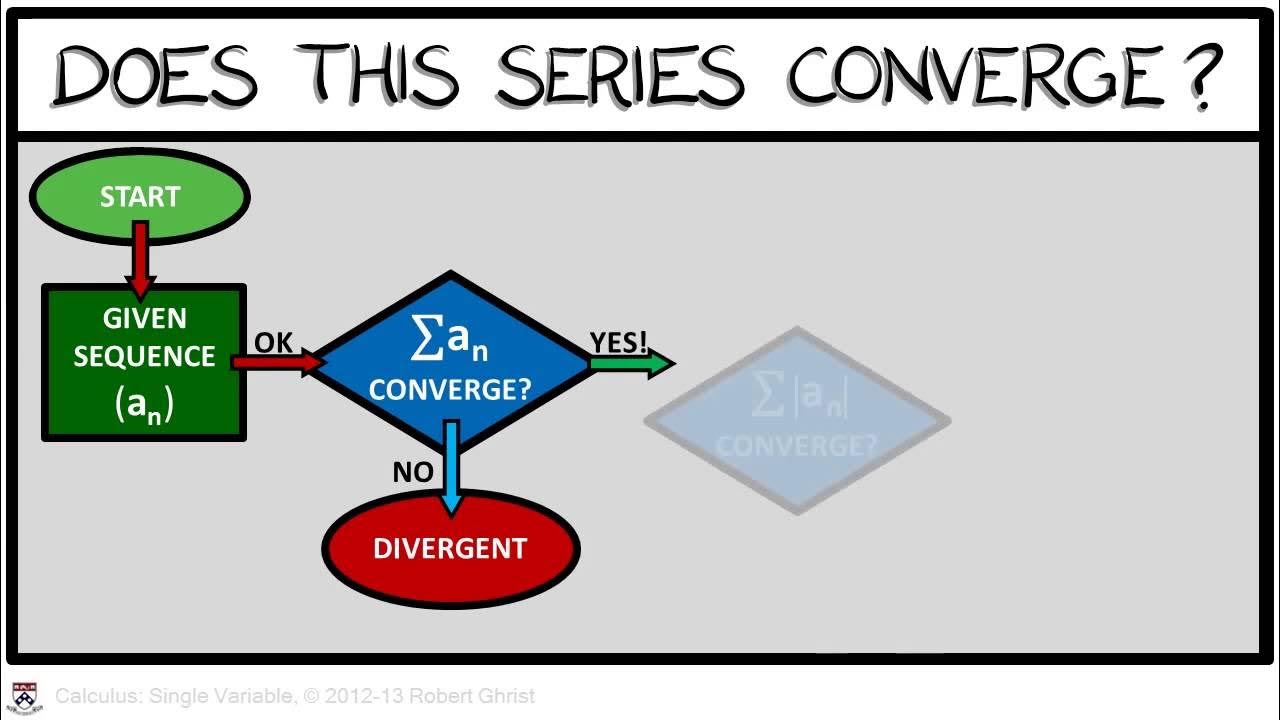
This paragraph introduces convergent series, which have a finite sum. It's hard to calculate the precise sum, so we use tricks like the integral test. The integral test says a decreasing, positive function's integral approximates the sum of its series. We apply this to 1/n^2 to estimate the sum is around 2.

05:01
😃 Using Comparison Tests on P-Series and Other Series

This paragraph discusses P-series, which are of the form 1/n^p. These converge if p>1 and diverge if p≤1. The comparison test compares a series to a known convergent/divergent series. If terms are smaller, it converges; if larger, it diverges. We apply this test to some examples.

Mindmap
Keywords
💡convergent series
A convergent series is a series where the sum of all the terms reaches a finite number. In the video, it is mentioned that 'convergent series, which are ones where the sum of all the terms in, the series is some finite number.' This is a key concept, as techniques like the integral test and comparison test are used to determine if a given series is convergent.
💡integral test
The integral test is a technique used to determine if a series is convergent and potentially estimate the sum. As explained, 'if we have some function, F, that is positive, continuous, and decreasing, from one to infinity, and we also have a sequence that is derived from this function...then the series that can be formed from this sequence...will be convergent only if the corresponding improper integral is convergent.' The integral test is demonstrated on the series with term 1/n^2.
💡P-series
A P-series refers to a series with terms in the form of 1/n^p, where p is some exponent. The video mentions 'Any series in the form of one over N raised to some exponent is called a P-series. This includes our first example, one over N squared.' Understanding convergence of P-series is important, as 'any P-series will be convergent if P is greater than one, and it will be divergent, if P is less than or equal to one.'
💡comparison test
The comparison test allows determining convergence for a series by comparing it to another series with known convergence. As explained, 'With this technique, we will take some series and compare it with a similar series that we know to be convergent or divergent.' An example is provided comparing a complex series to a geometric series to deduce convergence.
💡sequence
A sequence refers to an ordered list of numbers, often denoted {a_n}. Many series are formed from sequences, like A_n = f(n). The video discusses how 'if we have some function, F, that is...decreasing from one to infinity, and we also have a sequence that is derived from this function...then the series that can be formed from this sequence...will be convergent only if the...' integral test passes.
💡term
A term refers to one of the numbers in a sequence or elements in a series. When comparing series in the comparison test, for example, 'if every term in a series is smaller than each corresponding term in another series that is known to be convergent, then it too must be convergent.' Analyzing terms is key to assessing convergence.
💡sum
The sum refers to the result of adding all the terms in a series. A key aspect of convergent series is that 'the sum of all the terms in, the series is some finite number.' Techniques like the integral test can provide estimates of the sum.
💡rectangle method
This refers to the visual method of using rectangle areas under a curve to estimate series sums, as demonstrated in the 1/n^2 example. As explained, 'Let’s make some rectangles under the curve, each with a base of one and a height equal to the value of the function at the right endpoint of the interval...So the sum of the series will be approximately equal to one, to account for the first term...plus this improper integral'.
💡continuous
Continuous refers to a function with no breaks or gaps in its graph. This property is required for the integral test, as 'if we have some function, F, that is positive, continuous, and decreasing, from one to infinity...' then the integral test may be applied to related series.
💡decreasing function
A decreasing function has the property that f(x+1) < f(x), meaning the function values get smaller as x increases. This monotonic behavior allows using the integral test, as 'if we have some function, F, that is positive, continuous, and decreasing, from one to infinity...' then the integral test may be applied to related series.
Highlights

The study found a significant increase in life satisfaction for participants who practiced gratitude

Researchers noted the important role of positive emotions in building psychological resilience

The new therapy method led to reduced symptoms of anxiety and depression

Professor Smith introduced an innovative framework for understanding human motivation

The results challenged traditional economic models of rational decision making

Students who received growth mindset interventions showed significant academic improvements

The study provides evidence for the social learning theory of moral development

Dr. Lee proposed a novel mechanism to explain the etiology of the disease

Researchers identified several environmental risk factors for the condition

The results suggest possible applications for improving educational outcomes

Professor Clark presented a thought-provoking critique of contemporary economic policies

The study provides strong empirical support for the hypothesis

Dr. Wilson discussed the limitations of current treatment approaches and proposed alternative interventions

Researchers called for further investigation into the neurological underpinnings of creativity

The new policy offers several practical solutions for addressing urban poverty

Transcripts

Browse More Related Video

Tests for Convergence

Calculus BC – 10.6 Comparison Tests for Convergence

Direct comparison test | Series | AP Calculus BC | Khan Academy

Calculus Chapter 5 Lecture 53 Absolute & Conditional

Calculus 2 Lecture 9.6: Absolute Convergence, Ratio Test and Root Test For Series

Limit comparison test | Series | AP Calculus BC | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating: