Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (85 of 92) Transmission Coeff=? (3 of 6)

Michel van Biezen
14 May 201803:58
EducationalLearning
32 Likes 10 Comments

TLDRIn this lecture, the focus is on determining the transmission coefficient, which represents the probability of a particle passing through a barrier. The coefficient is defined as the ratio of the amplitude of the wave after the barrier to the amplitude before it. By setting up two equations based on boundary conditions and solving for the constants C and D, the lecture derives an expression for C in terms of D. The process involves factoring out common terms and simplifying the equations, ultimately leading to an equation that expresses C as a function of D, with the transmission coefficient dependent on the relative energy of the particle and the barrier, the mass of the particle, and Planck's constant.

Takeaways
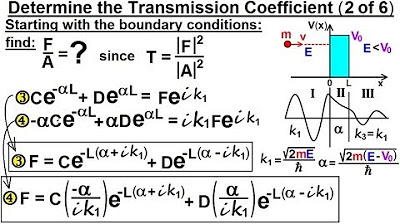
  • 🌟 The transmission coefficient is defined as the ratio of F/a, where F is the wave amplitude after passing through a barrier and a is the amplitude before reaching the barrier.
  • πŸ” The process involves solving for F in terms of a from boundary conditions, which are derived from previous equations discussed in the lecture series.
  • πŸ“ To find the ratio F/a, the two equations for F are set equal to each other, and terms are rearranged to isolate the coefficients C and D.
  • πŸ€” By moving all terms with a common exponent to one side, the exponential terms can be factored out, simplifying the equation.
  • 🧠 The coefficients of the exponential terms are then factored out, revealing the relationship between C and D in terms of the exponential factors.
  • πŸ“Š After factoring, the equation simplifies to allow the isolation of C in terms of D, which is expressed as C = D * e^(2*alpha*L), where alpha is determined by the relative energies and other physical properties of the particle and barrier.
  • 🌐 The wave number k1 is introduced as a key parameter in the analysis, representing the wave number in region 1.
  • πŸ”— The final step is to eliminate C from the equations by substituting it with the derived expression in terms of D, which will be the focus of the next lecture.
  • πŸ“š The lecture builds upon previous work, emphasizing the importance of understanding and applying boundary conditions to solve physical problems.
  • πŸŽ“ The mathematical manipulations are crucial for solving for the transmission coefficient, showcasing the depth of the quantum mechanics involved.
  • πŸš€ This analysis is part of a larger series of lectures, each building upon the previous to provide a comprehensive understanding of quantum barrier penetration.
Q & A

  • What is the transmission coefficient?

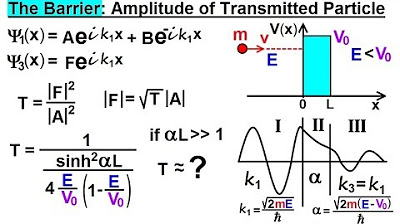
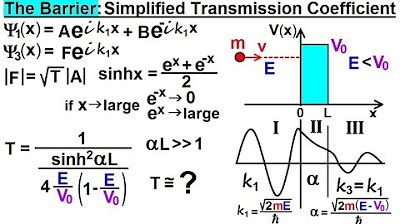
    -The transmission coefficient is the probability that a particle will pass through a barrier, defined as the ratio of the squared amplitude of the wave on the other side of the boundary to the squared amplitude of the wave before it reaches the boundary.

  • How is the transmission coefficient calculated?

    -The transmission coefficient is calculated by taking the ratio of F (the amplitude of the wave on the other side of the boundary) to a (the amplitude of the wave before it reaches the boundary) and then squaring this ratio.

  • What are the boundary conditions mentioned in the script?

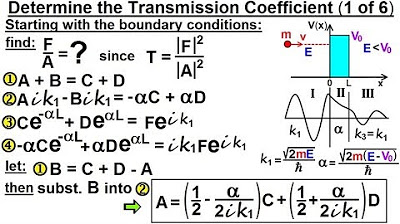
    -The boundary conditions mentioned in the script are the conditions that define the coefficients C and D, which are constants derived from the equations that describe the wave behavior at the boundary.

  • What is the significance of the constants C and D in the context of the script?

    -The constants C and D are coefficients that come from the boundary conditions and are used in the equations to solve for the transmission coefficient and the wave behavior at the boundary.

  • How does the script describe the process of solving for C in terms of D?

    -The script describes the process of solving for C in terms of D by setting the first equation of F equal to the second equation of F, rearranging the terms, and factoring out common elements to isolate C as a function of D.

  • What does the symbol 'alpha' represent in the context of the transmission coefficient?

    -In the context of the transmission coefficient, 'alpha' represents a term determined by the relative energy of the particle versus the energy of the barrier, the mass of the particle, and Planck's reduced constant (Δ§).

  • What is the role of the wave number 'k1' in the script's equations?

    -The wave number 'k1' is used to describe the behavior of the wave in region 1 and is a crucial part of the equations used to solve for the transmission coefficient and the constants C and D.

  • How does the script handle the simplification of the equations involving exponentials?

    -The script simplifies the equations involving exponentials by factoring out common terms, using the properties of exponents to cancel out similar terms, and then dividing by common denominators to further simplify the expressions.

  • What is the next step after finding C in terms of D according to the script?

    -The next step after finding C in terms of D is to eliminate C from all the equations by substituting C with the expression found in terms of D, which will be covered in the next video.

  • What does the final equation for C look like?

    -The final equation for C is C = D * e^(2 * alpha * L), where 'alpha' is determined by the relative energy of the particle and the barrier, 'L' is the width of the barrier, and 'e' is the base of the natural logarithm.

  • How does the relative energy of the particle and the barrier affect the transmission coefficient?

    -The relative energy of the particle and the barrier affects the transmission coefficient through the term 'alpha', which influences the exponential factor in the equation for C. Higher or lower relative energies will result in different transmission probabilities.

Outlines
00:00
πŸ“š Introduction to Transmission Coefficient and Wave Amplitudes

This paragraph introduces the concept of the transmission coefficient, which is the probability of a particle passing through a barrier. It explains that this coefficient is derived from the ratio of the squared amplitudes of the wave on either side of the boundary. The transmission coefficient is defined as F squared divided by a squared, where F is the amplitude of the wave beyond the boundary and a is the amplitude before reaching the boundary. The paragraph sets the stage for the mathematical process to find the ratio F/a, which is the main focus of the lecture series.

Mindmap
Keywords
πŸ’‘Transmission Coefficient
The transmission coefficient is a measure of the probability that a particle will pass through a barrier. In the context of the video, it is defined as the ratio of the squared amplitude of the wave after passing the barrier (F) to the squared amplitude before reaching the barrier (a). This coefficient is crucial in understanding quantum tunneling and wave behavior at boundaries.
πŸ’‘Amplitude
Amplitude in the context of waves refers to the maximum displacement of a point on the wave from its equilibrium position. In the video, amplitude is used to describe the strength of the wave before (a) and after (F) crossing a boundary. The ratio of these amplitudes is integral to determining the transmission coefficient.
πŸ’‘Quantum Tunneling
Quantum tunneling is a phenomenon in quantum mechanics where a particle can pass through a potential barrier that it classically shouldn't be able to overcome. The transmission coefficient discussed in the video is directly related to this phenomenon, as it quantifies the probability of a particle tunneling through a barrier.
πŸ’‘Boundary Conditions
Boundary conditions are specifications of the behavior of a function at the edges of its domain. In the context of the video, these conditions are used to set up equations that describe the wave function at the boundary of the barrier. Solving these equations helps in determining the coefficients C and D, which are essential for understanding wave behavior.
πŸ’‘Coefficients
In the context of the video, coefficients refer to the constants that appear in the equations derived from boundary conditions. C and D are specific coefficients that are solved for in the process of determining the transmission coefficient. They are essential in expressing the wave function in different regions.
πŸ’‘Wave Function
A wave function is a mathematical description of the quantum state of a system in quantum mechanics. It provides information about the probability amplitude of finding a particle in a particular quantum state. In the video, the wave function is discussed in relation to its behavior at boundaries and how it changes when a particle encounters a barrier.
πŸ’‘Exponential Functions
Exponential functions are mathematical functions where the base is a constant and the exponent is the variable. In the video, exponential functions are used to describe the wave function and its behavior when a particle encounters a barrier. The script manipulates these functions to solve for the coefficients and transmission coefficient.
πŸ’‘Complex Numbers
Complex numbers are numbers that consist of a real part and an imaginary part. In the context of the video, complex numbers are used in the expressions for the wave function and its coefficients. The imaginary unit 'i' is used to represent the square root of -1, which is essential in the equations describing quantum behavior.
πŸ’‘Solving Equations
Solving equations refers to the process of finding values for the variables that make the equation true. In the video, the speaker is solving a system of equations derived from boundary conditions to find the coefficients C and D, which are necessary for understanding the transmission coefficient.
πŸ’‘Factoring
Factoring is the process of breaking down a polynomial or an expression into a product of other expressions. In the video, factoring is used to simplify the equations and solve for the coefficients C and D by combining like terms and isolating variables.
πŸ’‘Canceling Out
Canceling out refers to the process of eliminating terms from an equation by performing equivalent operations on both sides, ultimately simplifying the equation. In the context of the video, this technique is used to isolate the variable C and express it in terms of D.
Highlights

The lecture focuses on finding the transmission coefficient by calculating the ratio F/a.

The transmission coefficient is defined as the probability of a particle passing through a barrier.

F represents the amplitude of the wave on the other side of the boundary, while a is the amplitude before reaching the boundary.

The ratio of the squared amplitudes (F^2/a^2) gives the transmission coefficient.

The next step involves setting two equations solved for F equal to one another.

These equations are derived from boundary conditions, which can be reviewed in previous videos.

The goal is to solve for C in terms of D, indicating that C is a function of D.

C and D are coefficients or constants from the boundary conditions.

By setting the first equation of F equal to the second, terms with a CM are moved to the left side.

The exponents -L*I*K1 + alpha are factored out, revealing they are the same on both sides.

A coefficient of 1 and a coefficient of -alpha/i*ka1 are factored out, resulting in 1 + alpha/i*ka1.

The same process is applied to the right side of the equation, factoring out terms with d*NM.

Both terms with the same exponent are factored out, resulting in a 1 and an alpha/i*ky.

The equation is then rearranged to isolate C, bringing terms with positive and negative exponents to the same side.

After simplifying the exponents and their denominators, C is expressed in terms of D, with the equation C = D * e^(2*alpha*L).

Alpha is determined by the relative energy of the particle versus the barrier, the mass of the particle, and H bar.

k1 is the wave number in region 1.

The final step is to eliminate C from all equations by substituting C with D times the derived expression.

The process leads to a clear equation with C expressed in terms of D, which will be the focus of the next video.

Transcripts

Browse More Related Video

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (84 of 92) Transmission Coeff=? (2 of 6)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (78 of 92) The Barrier: Amplitude

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (83 of 92) Transmission Coeff=? (1 of 6)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (79 of 92) Simplified Transmission Coeff.

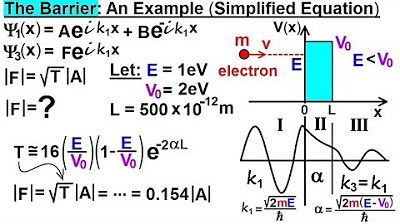
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (80 of 92) Transmission Coeff. Example

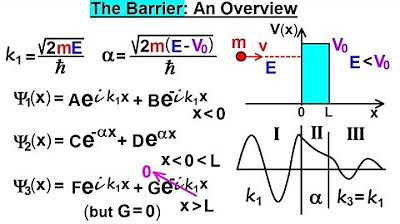
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (77 of 92) The Barrier: An Overview

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsTransmissionCoefficientWaveAmplitudeBoundaryConditionsParticleBarrierProbabilityCalculationPhysicsLectureOnlineEducationMathematicalAnalysisQuantumBarrier