Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (80 of 92) Transmission Coeff. Example

Michel van Biezen
9 May 201805:50
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational video, the focus is on calculating the amplitude of an electron as it attempts to pass through a potential barrier of 2 electron volts, with an initial energy of 1 electron volt. The barrier is 500 picometers wide. Using a simplified equation derived from quantum mechanics, the video demonstrates how to determine the transmission coefficient and subsequently the amplitude on the other side of the barrier. The calculation involves understanding the relationship between electron volts and joules, and the role of Planck's constant. The result indicates that the electron's amplitude on the far side of the barrier is significantly reduced, highlighting the probabilistic nature of quantum tunneling.

Takeaways
  • πŸ“Š The example demonstrates how to calculate the amplitude of a particle, specifically an electron, after it passes through a potential barrier.
  • πŸ’‘ The initial energy of the electron is 1 electron volt (eV), and it is attempting to pass through a barrier of 2 eV.
  • πŸ›‘ The barrier is 500 picometers (half a nanometer) wide, which is a critical parameter in the calculation.
  • πŸ“ The transmission coefficient is a key factor in determining the amplitude on the other side of the barrier.
  • πŸ”’ The equation for the transmission coefficient involves the ratio of the energies and the width of the barrier, along with the mass of the electron and Planck's constant.
  • 🌐 Units are not necessarily required to be in joules, as the calculation involves ratios and can be done in electron volts.
  • 🎯 The value of alpha (Ξ±) is derived from the square root of 2 times the mass of the electron and the energy difference.
  • πŸ“Œ The transmission coefficient is approximately 0.0238, indicating a significant drop in amplitude after passing through the barrier.
  • πŸ” The amplitude on the right side of the barrier is about 15% of that on the left side, showing a substantial reduction.
  • πŸš€ The process involves taking the square root of the transmission coefficient to find the relative amplitudes.
  • πŸ”„ A comparison between the approximate and original equations will be made to assess any significant differences in the outcome.
Q & A

  • What is the context of the example discussed in the transcript?

    -The context is a quantum mechanics problem involving an electron trying to pass through a potential barrier with a specific energy and barrier width.

  • What is the initial energy of the electron in the example?

    -The initial energy of the electron is 1 electron volt.

  • What is the height of the potential barrier in the example?

    -The height of the potential barrier is 2 electron volts.

  • What is the width of the potential barrier?

    -The width of the potential barrier is 500 picometers, or half a nanometer.

  • How is the transmission coefficient calculated in this example?

    -The transmission coefficient is calculated using a simplified equation derived from quantum mechanics principles, which involves the energy difference, the width of the barrier, and the mass of the electron.

  • What is the value of alpha in the equation?

    -Alpha is the product of the square root of 2 times the mass of an electron and the square root of the energy difference (2 eV - 1 eV), divided by the reduced Planck constant.

  • What is the role of the transmission coefficient in this problem?

    -The transmission coefficient indicates the probability or amplitude of the particle (electron) being found on the other side of the barrier after attempting to pass through it.

  • What is the approximate value of the transmission coefficient in this example?

    -The approximate value of the transmission coefficient is 0.00238, or about 0.023838 when calculated using the simplified equation.

  • How does the amplitude of the particle change after passing through the barrier?

    -The amplitude of the particle on the right side of the barrier is about 15% of the amplitude on the left side, as determined by taking the square root of the transmission coefficient.

  • Why is the unit of electron volts used instead of joules in this calculation?

    -Since the calculation involves taking ratios and the units cancel out, it is convenient to use electron volts directly without converting to joules.

  • What is the significance of comparing the approximate equation to the original equation?

    -Comparing the approximate equation to the original equation helps to verify the accuracy and validity of the approximation used, ensuring that the simplified model provides reliable results.

Outlines
00:00
🌟 Quantum Tunneling: Amplitude Calculation

This paragraph introduces a quantum mechanics problem focused on calculating the amplitude of a particle, specifically an electron, after it potentially passes through a barrier. The barrier has a width of 500 picometers and a height of 2 electron volts. The initial energy of the electron is given as 1 electron volt. The transmission coefficient, crucial for finding the amplitude on the other side of the barrier, is derived from a simplified equation. The calculation involves the mass of the electron, the difference in energy, and Planck's constant. The result indicates a high probability of transmission, with the amplitude on the right side of the barrier being approximately 15% of that on the left side.

05:01
πŸ“ˆ Energy and Amplitude: Simplified vs Original Equation

The second paragraph discusses the process of comparing a simplified equation to the original one for calculating the transmission coefficient and amplitude of a particle. The energy is related to the square root of the transmission coefficient, which is why taking the square root is necessary to find the relative amplitudes. The paragraph emphasizes the importance of this step in understanding quantum tunneling. It concludes by mentioning that a comparison between the approximate and original equations will be conducted to determine if there is a significant difference in the outcomes, thus validating the use of the simplified equation.

Mindmap
Keywords
πŸ’‘Electoral Line
The term 'Electoral Line' is likely a reference to the title of the video or the name of the series, which seems to be a program or channel that discusses scientific or mathematical concepts. It does not have a specific scientific definition within the context of the video script provided.
πŸ’‘Amplitude
Amplitude in the context of this video refers to the magnitude or strength of a wave or oscillation. Specifically, it is used to describe the energy of a particle, such as an electron, as it attempts to pass through a barrier. The amplitude on one side of the barrier is used to calculate the amplitude on the other side, indicating how much of the particle's initial energy is retained after it interacts with the barrier.
πŸ’‘Particle
In the provided script, a 'particle' refers to a subatomic entity, specifically an electron, which is being studied in the context of its interaction with a barrier. The term is used to discuss its initial energy, its attempt to pass through a barrier, and the resulting amplitude on the other side of the barrier.
πŸ’‘Barrier
The 'barrier' in this context is a hypothetical construct representing an obstacle that the particle (electron) must overcome. It is characterized by its energy requirement (2 electron volts) and its physical width (500 picometers). The barrier is used to model the interaction between the particle and the potential energy landscape it encounters.
πŸ’‘Transmission Coefficient
The 'transmission coefficient' is a quantitative measure used in quantum mechanics to describe the probability of a particle passing through a potential barrier. It is a crucial concept in understanding quantum tunneling and is calculated using a specific equation that takes into account the energy levels and the width of the barrier.
πŸ’‘Quantum Tunneling
Quantum tunneling is a phenomenon in quantum mechanics where a particle can pass through a potential barrier that it classically shouldn't be able to overcome due to insufficient energy. The video script discusses this concept by calculating the probability of an electron passing through a barrier, which is an application of quantum tunneling.
πŸ’‘Electron Volts
An 'electron volt' (eV) is a unit of energy commonly used in the field of physics, particularly in the context of electron beam instruments, X-ray generators, and particle physics. It represents the amount of kinetic energy gained or lost by a single electron when it passes through an electric potential difference of one volt. In the video, electron volts are used to quantify the initial energy of the electron and the energy required to pass through the barrier.
πŸ’‘Pico Meters
A 'pico meter' (pm) is a unit of length in the metric system, equal to one trillionth of a meter (10^-12 meters). In the context of the video, it is used to describe the width of the barrier that the electron is attempting to pass through, with the barrier being 500 picometers wide, which is equivalent to half a nanometer.
πŸ’‘Alpha (Ξ±)
In the context of this video, 'alpha' (Ξ±) represents a constant used in the calculation of the transmission coefficient for quantum tunneling. It is derived from the properties of the particle and the barrier, including the mass of the electron and the difference in energy between the initial and barrier energies.
πŸ’‘Planck's Constant
Planck's Constant is a fundamental constant in quantum mechanics, denoted by 'h' or 'Δ§' (h-bar), and it is related to the quantization of energy and the exchange of energy packets between particles. In the script, it is used as part of the calculation for 'alpha,' which is then used to determine the transmission coefficient and the amplitude of the particle after it interacts with the barrier.
πŸ’‘Mass Emission
The term 'mass emission' in the context of the video script refers to the process of emitting a particle, such as an electron, which has a certain mass. The mass of the electron is used in the calculation of 'alpha,' which is a crucial part of determining the transmission coefficient and the amplitude of the particle after it interacts with the barrier.
Highlights

The example involves determining the amplitude of a particle, specifically an electron, after it passes through a barrier.

The initial energy of the electron is 1 electron volt.

The barrier has a width of 500 picometers and a height of 2 electron volts.

The transmission coefficient is used to calculate the amplitude on the other side of the barrier.

The equation for the transmission coefficient is derived from previous work and involves the energy difference and barrier width.

Alpha, a parameter in the equation, is calculated using the mass of an electron and the energy difference.

The calculation involves converting electron volts to joules using the conversion factor of 1.602 x 10^-19 joules per electron volt.

The transmission coefficient is found to be approximately 0.0238 using the simplified equation.

The amplitude of the particle on the right side of the barrier is about 15% of that on the left side.

The energy of the particle is related to the square root of the transmission coefficient, which affects the amplitude.

The example demonstrates the practical application of quantum mechanics equations in calculating particle behavior.

The process includes checking the validity of the approximate equation against the original one for accuracy.

The use of electron volts as units simplifies the calculations without the need for conversion to joules.

The example provides a clear understanding of how to apply quantum mechanical equations to real-world scenarios.

The calculation involves complex mathematical operations, including square roots and exponentials.

The final result gives insight into the probability of an electron passing through a potential barrier.

Transcripts

Browse More Related Video

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (81 of 92) Transmission Coeff., Original Eq

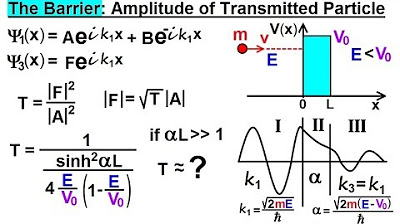
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (78 of 92) The Barrier: Amplitude

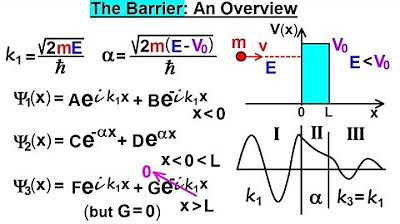
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (77 of 92) The Barrier: An Overview

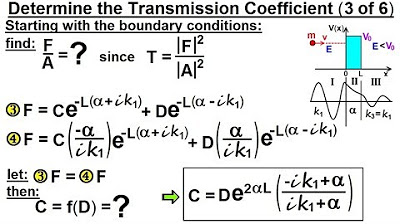
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (85 of 92) Transmission Coeff=? (3 of 6)

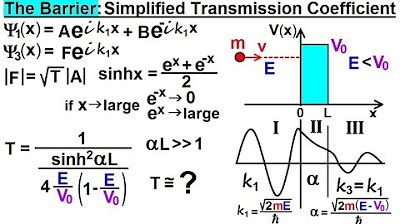
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (79 of 92) Simplified Transmission Coeff.

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (89 of 92) Which Penetrates Easier?

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Quantum MechanicsParticle TransmissionBarrier AnalysisAmplitude CalculationEnergy ConversionElectron VoltsPhysics TutorialMathematical ModelingSimplified EquationsTransmission Coefficient