Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (78 of 92) The Barrier: Amplitude

Michel van Biezen
7 May 201803:59
EducationalLearning
32 Likes 10 Comments

TLDRThis lecture delves into quantum mechanics, focusing on calculating the amplitude of a particle oscillating after passing through a barrier. It introduces the transmission coefficient, derived from the energy of the particle, the potential and width of the barrier. The lecture simplifies the equation for large barrier widths, showing how the transmission coefficient exponentially decreases with increasing barrier size, directly affecting the amplitude on the other side. Examples and further derivations are promised in upcoming videos.

Takeaways
  • 📐 The amplitude of a particle passing through a barrier depends on the particle's energy, the barrier's potential, and the barrier's width.
  • 🌐 The calculation focuses on the amplitude of oscillations in Region 3 compared to Region 1.
  • 🔄 Region 1 has two terms in its equation accounting for particles moving forward and reflected by the barrier.
  • 🚶‍♂️ Region 3 has one term, as particles only move in one direction after passing the barrier.
  • 🔢 The transmission coefficient (T) is the ratio of the squared amplitude in Region 3 to the squared amplitude in Region 1.
  • 🎢 The equation for the transmission coefficient is derived from the hyperbolic sine of alpha times L, where alpha is a constant and L is the barrier width.
  • 📉 The transmission coefficient decreases exponentially as the barrier width (L) increases.
  • 📶 A smaller transmission coefficient indicates a smaller amplitude on the other side of the barrier.
  • 🌟 The simplification of the transmission coefficient equation is applicable when alpha times L is significantly larger than one.
  • 📈 The script provides a foundation for calculating and understanding particle behavior in quantum mechanics scenarios.
  • 🔍 Upcoming videos will delve into the derivation of these equations and provide examples of their application.
Q & A

  • What is the main topic of the lecture?

    -The main topic of the lecture is the calculation of the amplitude of a particle passing through a barrier and the oscillations in the subsequent region.

  • What factors influence the amplitude of a particle after passing through a barrier?

    -The energy of the particle, the potential of the barrier, and the width of the barrier are the main factors influencing the amplitude.

  • How is the amplitude in Region three related to the amplitude in Region one?

    -The amplitude in Region three is related to the amplitude in Region one through the transmission coefficient, which is the ratio of their squared amplitudes.

  • What does the transmission coefficient (T) represent in this context?

    -The transmission coefficient (T) represents the probability of a particle passing through the barrier and continuing to oscillate in Region three.

  • How does the transmission coefficient (T) change with an increase in the width (L) of the barrier?

    -The transmission coefficient (T) decays exponentially as the width (L) of the barrier increases, indicating a smaller amplitude on the other side of the barrier.

  • What is the significance of the term 'hyperbolic sine of alpha times L' in the equation for the transmission coefficient?

    -The term 'hyperbolic sine of alpha times L' is part of the equation that describes the relationship between the transmission coefficient and the barrier parameters, simplifying to a more manageable form when alpha times L is large.

  • What happens when alpha times L becomes large relative to one?

    -When alpha times L becomes large relative to one, the equation for the transmission coefficient simplifies, allowing for an approximate calculation of T.

  • What is the role of the momentum of the particle in the transmission coefficient equation?

    -The momentum of the particle is part of the ratio used in the denominator of the transmission coefficient equation, influencing the value of T.

  • How can one determine when to use the simplified version of the transmission coefficient equation?

    -The simplified version of the transmission coefficient equation can be used when alpha times L is significantly larger than one, such as five or ten.

  • What will be covered in the upcoming videos?

    -The upcoming videos will provide more details on the derivation of the equations, examples of their application, and the differences between the simplified and full versions of the transmission coefficient equation.

Outlines
00:00
🌟 Quantum Barrier Penetration and Amplitude Analysis

This paragraph introduces the concept of quantum barrier penetration, focusing on the amplitude of a particle passing through a barrier. It discusses how the amplitude is influenced by the energy of the particle, the potential of the barrier, and the barrier's width. The main goal is to calculate the oscillation amplitude in Region 3 compared to Region 1. The Shrödinger equation is introduced for describing the two regions, with terms for reflected and transmitted particles. The transmission coefficient (T) is defined as the ratio of the amplitudes in Region 3 to Region 1, and its calculation is based on a complex equation involving the hyperbolic sine of alpha times L, where alpha and L are specific parameters related to the barrier. The paragraph also touches on the simplification of the transmission coefficient equation when alpha times L is large, and how the coefficient decays exponentially with increasing L, indicating a smaller amplitude on the other side of the barrier.

Mindmap
Keywords
💡Amplitude
Amplitude refers to the maximum displacement of a periodic wave from its equilibrium position, which in the context of the video, relates to the intensity of the particle's oscillations in different regions. It is a crucial concept as the video aims to calculate the amplitude of the oscillations of a particle after it passes through a barrier and compares it to the amplitude in another region. For example, the amplitude of the particle in Region one (a) is compared to the amplitude in Region three (F), with the latter being the focus for understanding transmission through the barrier.
💡Particle
In the context of the video, a particle refers to a small, often subatomic, entity that is subject to quantum mechanical effects. The behavior of the particle, particularly its ability to pass through a barrier (tunnel effect), is the central focus of the lecture. The particle's energy, momentum, and interaction with the potential barrier are key to understanding the transmission coefficient and the resulting amplitude in different regions.
💡Barrier
A barrier in this context is a region of space with a potential that hinders or prevents the passage of particles. The properties of the barrier, such as its width and potential, significantly affect the transmission coefficient and the amplitude of the particle's oscillations in different regions. The barrier is essential for the discussion of quantum tunneling and the calculation of the transmission coefficient.
💡Transmission Coefficient
The transmission coefficient is a measure of the probability that a particle will pass through a barrier, as opposed to being reflected. It is calculated using the amplitudes in different regions and is crucial for understanding quantum tunneling. The video focuses on calculating this coefficient to determine the relative amplitude of a particle's oscillations after passing through a barrier.
💡Hyperbolic Sine
Hyperbolic sine is a mathematical function that is analogous to the ordinary sine function but involves exponentiation with the imaginary unit 'i'. In the context of the video, it appears in the equation for the transmission coefficient, which is used to describe the behavior of particles in quantum mechanics, particularly in relation to quantum tunneling. The hyperbolic sine function is integral to the derivation of the transmission coefficient and the simplification of the equation for large values of alpha times L.
💡Energy
Energy, in the context of the video, refers to the property of the particle that allows it to do work or to move through a potential barrier. The energy of the particle is a critical factor in determining the transmission coefficient and the amplitude of the particle's oscillations in different regions. It is a fundamental concept in quantum mechanics and is used to calculate the probability of a particle passing through a barrier.
💡Potential
Potential in this context refers to the energy state that a particle would have if it were located at a particular point within a force field, such as the barrier mentioned in the video. The potential of the barrier is a key factor in the transmission coefficient equation, affecting the probability of a particle passing through the barrier. It is a fundamental concept in physics, particularly in the study of electric and gravitational fields, and is essential for understanding the behavior of particles in quantum mechanics.
💡Width of the Barrier
The width of the barrier is the spatial extent of the region that acts as a potential obstacle for the particle. It is a significant parameter in the transmission coefficient equation, influencing the probability of a particle passing through the barrier. The width, along with the potential and energy of the particle, is used to calculate the transmission coefficient and understand the quantum tunneling effect.
💡Quantum Tunneling
Quantum tunneling is a quantum mechanical phenomenon where a particle can pass through a potential barrier that would be classically insurmountable. The video's discussion of the transmission coefficient and the amplitude of a particle's oscillations after passing through a barrier is directly related to this phenomenon. Quantum tunneling is a fundamental concept in quantum mechanics and has practical applications in technologies such as semiconductors and quantum computing.
💡Momentum
Momentum in physics is the product of a particle's mass and velocity and is a measure of its motion. In the context of the video, the momentum of the particle is related to its energy and is used in the calculation of the transmission coefficient. The concept of momentum is crucial in understanding the behavior of particles, especially in the quantum realm where it interacts with potential barriers.
Highlights

The lecture focuses on calculating the amplitude of a particle passing through a barrier.

The amplitude depends on the energy of the particle, the potential of the barrier, and the width of the barrier.

The aim is to compare the amplitude of oscillations in Region 3 to that in Region 1.

Region 1 has two terms in its equation due to the possibility of particle reflection.

Region 3 has only one term as there's no reflection after passing the barrier.

The transmission coefficient is the ratio of the square of the amplitude in Region 3 to that in Region 1.

The amplitude in Region 3 is the square root of T times the amplitude in Region 1.

The transmission coefficient is defined by a complex equation involving hyperbolic sine and other factors.

The equation for the transmission coefficient is 1 divided by (1 plus hyperbolic sine of alpha times L).

Alpha is defined by the energy of the particle and the potential of the barrier.

The transmission coefficient simplifies when alpha times L is much larger than one.

The coefficient decays exponentially as L becomes large, indicating a smaller amplitude.

A smaller transmission coefficient corresponds to a smaller amplitude on the other side of the barrier.

The lecture will provide examples and details on calculating these values in future videos.

The derivation of the transmission coefficient equation will be covered in upcoming content.

The current content provides equations to calculate amplitude on one side of the barrier relative to the other.

Given energy (e), potential (V), and barrier width (L), one can calculate the amplitude ratio.

Transcripts

Browse More Related Video

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (85 of 92) Transmission Coeff=? (3 of 6)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (77 of 92) The Barrier: An Overview

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (79 of 92) Simplified Transmission Coeff.

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (80 of 92) Transmission Coeff. Example

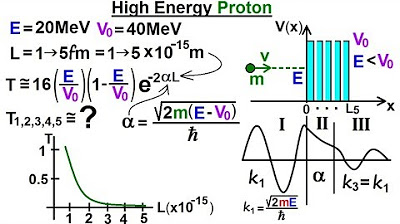
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (90 of 92) A High Energy Proton

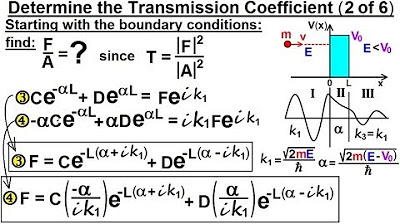
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (84 of 92) Transmission Coeff=? (2 of 6)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumMechanicsParticleAmplitudeTransmissionCoefficientBarrierPenetrationEnergyMomentumHyperbolicFunctionsPhysicsLectureEducationalContentMathematicalAnalysisWaveOscillations