Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (84 of 92) Transmission Coeff=? (2 of 6)

Michel van Biezen
13 May 201803:32
EducationalLearning
32 Likes 10 Comments

TLDRIn this online lecture, the focus is on calculating the transmission coefficient, which represents the probability of a particle passing through a barrier. The process involves solving a system of equations derived from boundary conditions, with the aim of eliminating constants B and C to express the transmission coefficient in terms of the amplitudes of oscillations in different regions. The lecture demonstrates how to solve for F using equations 3 and 4, and sets up the stage for the next step, which is to eliminate C by setting these equations equal to each other and solving for C in terms of D.

Takeaways
  • 📚 The lecture focuses on calculating the transmission coefficient using boundary conditions and wave functions.
  • 🔍 The process involves solving a set of equations with three functions that describe wave behavior across different regions.
  • 💡 The constant B was previously eliminated from the equations by using its equivalent, which is C plus D minus a constant.
  • 📈 Equations 3 and 4 are used to solve for the constant F, which represents the amplitude of oscillations in regions 1 and 3.
  • 🌟 The transmission coefficient is the ratio of F squared to a squared, representing the probability of a particle passing through a barrier.
  • 🔢 In solving for F, the third equation is manipulated to isolate F, resulting in a division by a term involving the exponential of I k1 L.
  • 🔄 By setting the expressions for F from equations 3 and 4 equal to each other, we can solve for the constant C in terms of D.
  • 📌 The next step is to eliminate C from the equations by expressing it as a function of the constant D.
  • 🎓 The lecture series will continue in the next video, where the process of eliminating C and solving the equations will be completed.
  • 🤔 The mathematical process involves careful manipulation of exponential terms and factoring to simplify the equations.
  • 📊 The final goal is to understand the quantum mechanical behavior of particles in the context of potential barriers.
Q & A

  • What is the main goal of the lecture?

    -The main goal of the lecture is to find the transmission coefficient by analyzing the boundary conditions and equations related to wave functions and amplitudes across different regions.

  • What is the significance of the transmission coefficient in this context?

    -The transmission coefficient represents the probability of a particle making it through a barrier, which is a crucial concept in quantum mechanics.

  • How many regions are considered in this lecture for the wave functions?

    -Three regions are considered: Region 1, where the amplitude of oscillations is represented by 'a', and Region 3, where the amplitude is represented by 'F'.

  • What was the first step in the previous video that was mentioned in the transcript?

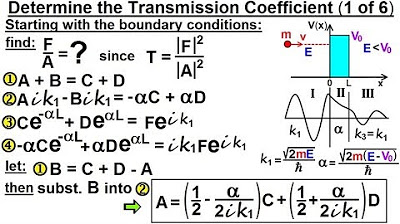
    -The first step in the previous video was to eliminate the constant 'B' by using its equivalent 'C plus D minus' and plugging it into the equations.

  • What does the term 'e to the I k1 L' represent in the equations?

    -'e to the I k1 L' represents an exponential term in the equations, which is part of the mathematical formulation used to describe wave behavior in different regions.

  • How are equations 3 and 4 used to solve for 'F'?

    -Equations 3 and 4 are solved for 'F' by isolating 'F' on one side of each equation, then setting the right sides equal to each other to find the relationship between the constants 'C' and 'D'.

  • Why is it necessary to solve for 'C' in terms of 'D'?

    -Solving for 'C' in terms of 'D' allows for the elimination of 'C' from the equations, simplifying the process of finding the transmission coefficient.

  • What happens when you factor out a negative 'L' from the exponents in the equations?

    -Factoring out a negative 'L' from the exponents simplifies the equations, resulting in expressions that are easier to manipulate and solve for the constants.

  • What is the next step after solving for 'F' using equations 3 and 4?

    -The next step is to set the two equations equal to each other to solve for 'C' in terms of 'D', which will then allow for the elimination of 'C'.

  • How does the process of eliminating constants help in understanding the transmission coefficient?

    -Eliminating constants simplifies the mathematical model, making it easier to calculate the transmission coefficient and understand the probability of a particle passing through a barrier.

  • What is the role of the constants 'alpha' and 'I K 1 L' in the equations?

    -The constants 'alpha' and 'I K 1 L' are coefficients in the equations that represent specific physical quantities or parameters related to the wave function behavior in the given regions.

Outlines
00:00
📚 Introduction to Transmission Coefficient Calculation

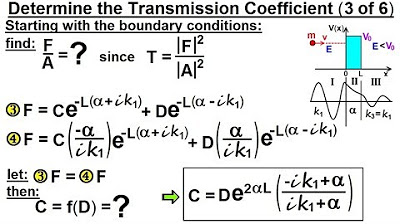
This paragraph introduces the goal of the lecture, which is to calculate the transmission coefficient. It explains the process of using boundary conditions and three functions to reach regions 1, 2, and 3. The paragraph also discusses the previous elimination of constant B and the current focus on solving equations for constant F, which represents the amplitude of oscillations in different regions and is crucial for determining the transmission coefficient, representing the probability of a particle passing through a barrier.

Mindmap
Keywords
💡Transmission Coefficient
The transmission coefficient is a measure used in quantum mechanics to describe the probability of a particle passing through a potential barrier. In the context of the video, it is calculated by taking the ratio of the squared amplitudes of oscillations in different regions. The script mentions finding this coefficient by solving a set of equations, which is crucial for understanding particle behavior in the presence of a barrier.
💡Boundary Conditions
Boundary conditions are constraints or specifications that are applied at the edges of a problem domain. In the video, they are used to define the behavior of wave functions on both sides of a barrier. These conditions are essential for setting up the equations that will later be solved to find the transmission coefficient, as they ensure the wave functions are physically meaningful and continuous across the barrier.
💡Wave Functions
Wave functions are mathematical descriptions of the quantum state of a system. They provide information about the probability of finding a particle in a particular state. In the video, wave functions are used to describe the behavior of particles in different regions, with the aim of finding the transmission coefficient. The wave functions are represented by the functions in the equations that are being solved.
💡Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that describes the behavior of matter and energy at the atomic and subatomic scales. The video's content is rooted in quantum mechanics principles, as it deals with the transmission of particles through barriers, a classic problem in the field. The transmission coefficient, a key concept in the video, is a direct application of quantum mechanics to understand particle tunneling.
💡Amplitude of Oscillations
The amplitude of oscillations refers to the maximum displacement of a wave from its equilibrium position. In the context of the video, it represents the strength of the wave function in a given region. The transmission coefficient is related to the ratio of the squared amplitudes of oscillations in different regions, indicating the probability of a particle's transmission through a barrier.
💡Potential Barrier
A potential barrier is a region in space where the potential energy is higher than the energy of a particle. In quantum mechanics, particles can tunnel through such barriers, even if classically they do not have enough energy to overcome the barrier. The video focuses on calculating the probability of this quantum tunneling effect through the transmission coefficient.
💡Equations
Equations are mathematical statements that assert the equality of two expressions. In the video, equations are used to model the behavior of wave functions and to calculate the transmission coefficient. The process involves solving these equations for specific variables, which allows for the determination of the transmission coefficient.
💡Constants
Constants are values that do not change. In the context of the video, constants like B, C, and D are coefficients in the equations that describe the wave functions. These constants are determined by solving the equations, and they play a crucial role in calculating the transmission coefficient.
💡Factoring
Factoring is the process of breaking down a polynomial or an expression into a product of other expressions. In the video, factoring is used as a mathematical technique to simplify the equations and solve for the constants involved in the transmission coefficient calculation.
💡Exponential Functions
Exponential functions are mathematical functions of the form e^x, where e is the base of the natural logarithm and x is the variable. They are fundamental in many areas of mathematics, including quantum mechanics. In the video, exponential functions appear in the equations that describe the wave functions and are used to calculate the transmission coefficient.
💡Tunneling
Tunneling is a quantum mechanical phenomenon where a particle can pass through a potential barrier that it classically could not overcome. The transmission coefficient is directly related to the probability of tunneling occurring. The video's main focus is on calculating this probability using the transmission coefficient.
Highlights

The lecture focuses on finding the transmission coefficient.

The process starts with boundary conditions on both sides of the barrier.

Three functions are used, reaching from region 1, 2, and 3.

In the previous video, constant B was eliminated from the equations.

Equations 3 and 4 will now be used to solve for F.

F is a constant representing the amplitude of oscillations in region three.

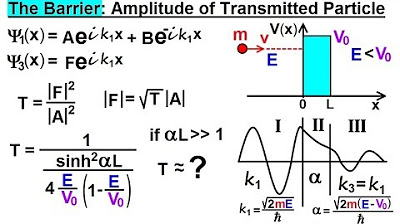
The ratio of the squared amplitudes is the transmission coefficient.

The transmission coefficient is also the probability of a particle making it through the barrier.

Equation 3 is solved for F, resulting in an expression involving e to the power of I k1 L.

Equation 4 is also solved for F, with a similar process.

The two equations for F are then set equal to each other to solve for C in terms of D.

By setting the equations equal, we can eliminate the constant C by replacing it with its equivalent function of D.

The process involves factoring out negative L from the exponential terms.

The end goal is to simplify the equations to understand particle transmission through the barrier.

The lecture is part of a series, with the continuation to be covered in the next video.

The mathematical approach is based on solving a system of equations for specific constants.

The transmission coefficient has practical applications in quantum mechanics.

Transcripts

Browse More Related Video

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (85 of 92) Transmission Coeff=? (3 of 6)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (83 of 92) Transmission Coeff=? (1 of 6)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (78 of 92) The Barrier: Amplitude

Algebraic Method for Balancing Chemical Equation

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (66 of 92) B=? C=? in terms of E & V0

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (72 of 92) R=? T=? V0=(1/4)E (Ex. 2 of 4)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Quantum MechanicsTransmission CoefficientBoundary ConditionsWave FunctionsBarrier AnalysisMathematical PhysicsLecture SeriesEducational ContentParticle BehaviorProbability Theory