Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (74 of 92) R=? T=? V0=(3/4)E,.(Ex. 4 of 4)

Michel van Biezen
3 May 201804:56
EducationalLearning
32 Likes 10 Comments

TLDRThis lecture explores the behavior of particles encountering potential steps in a quantum mechanics context. As the step's energy approaches that of the particle, reflection coefficients are calculated to determine the percentage of particles reflected. Intriguingly, even when the potential step's energy is 99% of the particle's energy, only 66.9% of particles are reflected, highlighting the counterintuitive nature of quantum mechanics compared to classical mechanics.

Takeaways
  • 📈 When the potential step's energy approaches the particle's energy, the reflection coefficient changes significantly.
  • 🔢 At 3/4 the energy of the particle, 11.1% of particles are reflected.
  • 🔽 As the potential step's energy increases to 90% of the particle's energy, the reflection coefficient rises to 27%.
  • 🔼 Conversely, 73% of particles are transmitted when the potential step is at 90% of the particle's energy.
  • 🌟 At 99% energy equivalence, a surprising 66.9% of particles are reflected, with only 33.1% transmitted.
  • 💡 Quantum mechanics differs from classical mechanics in how particles interact with potential steps.
  • 🚧 Even when the potential step's energy is less than the particle's energy, quantum mechanics predicts reflection.
  • 📊 The reflection coefficient is calculated using the formula 1 - (1 - (potential/energy)^2)^0.5.
  • 🌐 The results are a direct application of quantum tunneling, a phenomenon not accounted for in classical physics.
  • 🤔 The lecture explores the boundary between quantum and classical behavior in terms of particle energy and potential steps.
  • 📚 The script serves as an educational resource for understanding the principles of quantum mechanics and their implications.
Q & A

  • What is the main topic of the lecture?

    -The main topic of the lecture is the behavior of particles when encountering a potential step in quantum mechanics, specifically how the reflection coefficient changes as the potential step's energy approaches the particle's energy.

  • How does the potential step's energy relate to the particle's energy in the first case discussed?

    -In the first case, the potential step's energy is 3/4 (75%) of the particle's energy.

  • What is the formula used to calculate the reflection coefficient?

    -The formula used to calculate the reflection coefficient is R = (1 - (V/E)^2) / (1 + (V/E)^2), where V is the potential step's energy and E is the particle's energy.

  • What percentage of particles are reflected when the potential step is 3/4 the energy of the particle?

    -When the potential step is 3/4 the energy of the particle, approximately 11.1% of the particles are reflected.

  • How does the reflection coefficient change when the potential step's energy is 90% of the particle's energy?

    -When the potential step's energy is 90% of the particle's energy, the reflection coefficient is approximately 27%.

  • What is the classical mechanics expectation for particle behavior when the potential step's energy is less than the particle's energy?

    -In classical mechanics, if the potential step's energy is less than the particle's energy, 100% of the particles would continue past the step without reflection.

  • What happens when the potential step's energy is 99% of the particle's energy in quantum mechanics?

    -When the potential step's energy is 99% of the particle's energy, about 66.9% of the particles are reflected, and approximately 33.1% are transmitted.

  • How does quantum mechanics differ from classical mechanics in the case where the potential step's energy is 99% of the particle's energy?

    -In quantum mechanics, with the potential step's energy at 99% of the particle's energy, 33.1% of the particles are still transmitted, whereas in classical mechanics, 100% of the particles would be transmitted with no reflection.

  • What is the significance of the reflection coefficient in quantum mechanics?

    -The reflection coefficient in quantum mechanics is significant as it quantifies the probability of a particle being reflected by a potential step, which is a key concept in understanding wave-particle duality and quantum behavior.

  • How does the potential step affect the transmission of particles in quantum mechanics?

    -In quantum mechanics, the potential step affects the transmission of particles by altering their wavefunction, which in turn affects the probability of reflection and transmission. As the potential step's energy approaches the particle's energy, the reflection coefficient increases, and the transmission decreases.

  • What is the role of the potential step in quantum mechanics?

    -The potential step in quantum mechanics serves as a model to study the wave-like behavior of particles. It helps in understanding how particles interact with energy barriers and how their behavior differs from classical mechanics, particularly in terms of reflection and transmission probabilities.

Outlines
00:00
🌟 Quantum Mechanics and Particle Reflection

This paragraph delves into the behavior of particles in the realm of quantum mechanics, particularly focusing on how the energy of a potential step affects the reflection coefficient. The discussion begins with a scenario where the potential step's energy is 3/4 that of the particle, then progresses to 90% and finally 99% of the particle's energy. Through calculations using a simplified equation, it's revealed that as the potential step's energy approaches that of the particle, the percentage of reflected particles decreases. Notably, when the potential step is 99% the energy of the particle, only 66.9% of the particles are reflected, contrasting with classical mechanics where 100% of particles would be transmitted. This highlights the intriguing and counterintuitive nature of quantum mechanics.

Mindmap
Keywords
💡Potential Step
A potential step is a type of energy barrier in quantum mechanics that represents a sudden change in potential energy. In the context of the video, it is used to illustrate how particles interact with an energy barrier that is a fraction of their own energy. The script discusses varying the energy of the potential step relative to the energy of the particle to observe the reflection and transmission behavior.
💡Reflection Coefficient
The reflection coefficient is a measure of the probability that a particle will be reflected by a potential barrier. In quantum mechanics, this coefficient is not simply determined by the energy difference between the particle and the barrier but also depends on the wave-like nature of the particle. The video script calculates the reflection coefficient for different energy levels of the potential step.
💡Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that describes the behavior of matter and energy at very small scales, such as atomic and subatomic particles. It is characterized by phenomena like wave-particle duality and quantum superposition, which are not observed in classical mechanics. The video script uses quantum mechanics principles to explain the unexpected behavior of particles encountering a potential step.
💡Energy
In the context of the video, energy refers to the total energy possessed by a particle, which can be kinetic or potential. The energy of a particle is crucial in determining its behavior when encountering a potential step, such as whether it will be transmitted or reflected.
💡Particle
A particle, in the context of this video, refers to a subatomic entity such as an electron or photon that is being studied within the framework of quantum mechanics. The behavior of these particles when interacting with potential steps is the focus of the lecture.
💡Transmission
Transmission in the context of the video refers to the process by which particles pass through a potential step. Unlike reflection, where particles are bounced back, transmission indicates that particles continue past the potential step.
💡Classical Mechanics
Classical mechanics is a branch of physics that deals with the motion of macroscopic objects under the influence of forces. It is based on classical concepts of particles and does not account for the quantum effects observed at the atomic and subatomic levels. The video script contrasts classical mechanics with quantum mechanics to highlight the differences in particle behavior.
💡Square Root
The square root is a mathematical operation that finds the value which, when multiplied by itself, gives the original number. In the context of the video, the square root is used in the formula to calculate the reflection coefficient for particles encountering a potential step.
💡Fraction
A fraction in the video refers to a part of a whole, represented numerically as one number divided by another. It is used to express the ratio of the potential step's energy to the particle's energy, which is crucial in determining the reflection coefficient.
💡Wave-Particle Duality
Wave-particle duality is a fundamental concept in quantum mechanics that states that particles exhibit both wave-like and particle-like properties. This duality is what allows for the calculation of probabilities, such as the reflection coefficient, which cannot be explained by classical mechanics alone.
💡Quantum Superposition
Quantum superposition is a principle in quantum mechanics where a particle can exist in multiple states simultaneously until it is measured. This concept is related to the video's theme as it underlies the probabilistic nature of particle behavior when encountering a potential step.
Highlights

The lecture explores the impact of increasing the potential step's energy relative to the particle's energy on the reflection coefficient.

The potential step's energy is initially set at 3/4 the energy of the particle to observe the reflection.

When the potential step is 3/4 the energy of the particle, 11.1% of the particles are reflected.

The potential step's energy is then increased to 90% of the particle's energy.

At 90% energy equivalence, only 27% of the particles are reflected, while 73% are transmitted.

In classical mechanics, all particles would pass the step if the potential energy is less than the particle's energy.

The potential step's energy is further increased to 99% of the particle's energy.

At 99% energy equivalence, 66.9% of the particles are reflected, and 33.1% are transmitted.

In contrast to quantum mechanics, in classical physics, all particles would be transmitted at 99% energy equivalence.

The quantum mechanics model shows that even when the potential step's energy is greater than the particle's energy, a significant number of particles are still transmitted.

The reflection coefficient is calculated using the simplified equation 1 - sqrt(1 - (potential energy / particle energy)^2).

The lecture demonstrates the counterintuitive nature of quantum mechanics compared to classical mechanics.

The study provides insights into particle behavior at energy thresholds in quantum states.

The results show that quantum mechanics allows for particle transmission even when facing high energy barriers.

The lecture's findings are a practical application of quantum mechanics principles.

The mathematical approach to calculating reflection coefficients is detailed for different energy ratios.

The lecture's content is a valuable resource for understanding quantum mechanics' unique behaviors.

Transcripts

Browse More Related Video

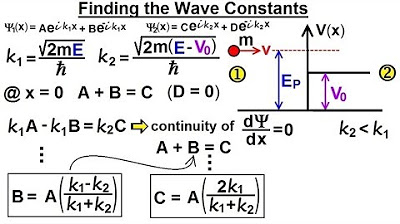
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (65 of 92) Wave Constants B=? C=?

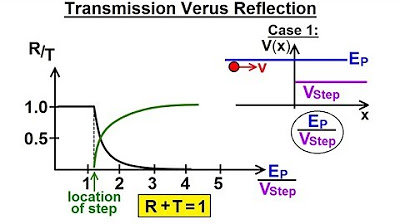
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (62 of 92) Transmission vs Reflection

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (64 of 92) Transmission-Reflection (Q.M.)

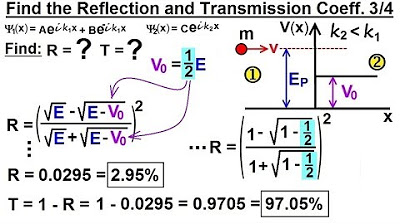
Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (73 of 92) R=? T=? V0=(1/2)E (Ex. 3 of 4)

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (61 of 92) Reflection & Transmission

Physics - Ch 66 Ch 4 Quantum Mechanics: Schrodinger Eqn (76 of 92) Penetration Depth V0, E: Ex.

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
QuantumPhysicsParticleReflectionPotentialBarriersEnergyComparisonQuantumBehaviorClassicalVsQuantumMysteriesOfQuantumPhysicsExperimentsEducationalContentScienceLecture