How I would explain Calculus to a 6th grader
TLDRThe video script demystifies calculus for a sixth-grade audience, explaining its fundamental concepts of integration and differentiation. It begins by relating basic area calculations to the more complex task of finding the area under a squiggly curve, illustrating how calculus uses infinitesimally small rectangles to approximate and precisely determine areas. The script then introduces the concept of derivatives to explain instantaneous velocity, showing how calculus can capture the precise momentary speed of an accelerating object. The video aims to inspire appreciation for calculus's ability to solve real-world problems beyond traditional formulas.
Takeaways
- 📚 Calculus can demystified for anyone, regardless of age or math level.
- 🧠 The essence of calculus can be understood with the mathematical concepts learned up to the sixth grade.
- 📊 Calculus enables the precise calculation of areas and volumes for any shape, even those without a direct formula.
- 🔍 The process of finding the area under a curve involves breaking the shape into infinitesimally small rectangles and summing their areas.
- 🚗 Calculus is essential for determining instantaneous velocity, especially for objects undergoing acceleration.
- 📈 Integration, represented by the integral symbol, is the calculus concept used to find the area under a curve.
- 🔄 The derivative, represented by d/dx or d/dy, is the calculus concept used to find instantaneous rates, such as velocity.
- 🌟 Calculus has real-world applications, such as calculating the speed of a falling object or the area of complex shapes.
- 👨🏫 The speaker, John, is a math educator who has created comprehensive online math courses and offers resources for learning math.
- 🔗 Additional math resources, including notes and courses, are available through links provided in the video description.
- 🌐 Encouragement is given to explore calculus despite its challenging nature, as it can solve complex problems with practical applications.
Q & A
What is the main objective of the video?
-The main objective of the video is to demystify calculus and help viewers appreciate its value, especially for those who might find it intimidating or complex.
Why does the speaker believe that sixth graders have enough mathematical knowledge to understand the essence of calculus?
-The speaker believes that the mathematical concepts learned in sixth grade, such as understanding areas of basic shapes and the idea of formulas, provide a solid foundation to grasp the fundamental ideas behind calculus.
How does calculus help in finding the area of irregular shapes?
-Calculus allows for the precise calculation of areas for any shape, including irregular ones, by using concepts like breaking the shape into infinitesimally small rectangles and summing their areas to estimate the total area under a curve.
What is the integral symbol in calculus, and what does it represent?
-The integral symbol in calculus represents the sum of an infinite number of infinitesimally small rectangles under a curve, which is used to find the exact area under the curve or function.
How does the concept of 'area under a curve' relate to real-world problems?
-The concept of area under a curve can be applied to real-world problems such as calculating the distance traveled by a car at varying speeds over time or determining the rate at which an object falls under gravity.
What is the second problem that calculus helps to solve, according to the speaker?
-The second problem that calculus helps to solve is finding the instantaneous velocity of an object that is accelerating, which cannot be determined using average speed and time or distance formulas.
What is the derivative in calculus, and what does it represent?
-The derivative in calculus represents the rate of change of a function with respect to its variable, often used to calculate instantaneous velocity or the slope of a curve at a particular point.
How does the speaker suggest one should approach learning calculus?
-The speaker suggests that one should approach learning calculus with an open mind, without pressure, and with a willingness to enjoy the concepts and appreciate its ability to solve complex real-world problems.
What is the significance of calculus in solving real-world problems?
-Calculus is significant in solving real-world problems because it provides a mathematical framework to handle issues involving rates of change and areas under curves, which are common in fields like physics, engineering, and economics.
How does the speaker describe the process of estimating the area under a squiggly shape?
-The speaker describes the process of estimating the area under a squiggly shape by breaking it down into smaller and smaller rectangles, which, when added together, provide a closer and closer estimate of the actual area, ultimately leading to a precise calculation using calculus.
Outlines
📚 Introducing Calculus to Sixth Graders
The speaker begins by addressing the challenge of explaining calculus to a sixth grader. Although calculus is not typically taught at that grade level, the foundational concepts learned by that time can provide a basis for understanding calculus. The speaker aims to demystify calculus and highlight its practical applications, emphasizing that it can help solve problems involving complex shapes and areas. The introduction also includes a brief background on the speaker's qualifications and the resources available for those needing math assistance.
📈 Understanding Calculus Through Shapes and Areas
The speaker delves into the concept of calculating areas of various shapes, starting with simple figures like circles, rectangles, and triangles, and their respective formulas. The discussion then moves to more complex shapes, such as a 'squiggly' curve, to illustrate the limitations of basic formulas. Calculus is introduced as a tool for finding the exact area of irregular shapes. The speaker explains how using rectangles to approximate areas can lead to more precise calculations, setting the stage for understanding the fundamental principles of calculus.
🔢 The Power of Infinitesimals in Calculus
The speaker continues the explanation of calculus by focusing on the concept of infinitesimals. By using an infinite number of infinitesimally thin rectangles under a curve, one can obtain the precise area under the curve. This is the essence of integration in calculus. The speaker introduces the calculus notation, explaining how it represents the summation of these infinite rectangles from a starting point to an endpoint, effectively describing the area under the curve defined by a function.
🚗 Calculus and Instantaneous Velocity
The speaker introduces the second major concept in calculus: the derivative, which is used to calculate instantaneous velocity. Using the example of a car accelerating from 0 to 80 miles per hour, the speaker explains that calculus is necessary to determine the car's exact speed at any given moment during acceleration. The concept is further illustrated with the example of a ball dropped from a building, emphasizing that calculus can provide the instantaneous velocity at any point in time, a task not possible with basic speed, distance, and time formulas.
🌟 The Value and Applications of Calculus
In the concluding paragraph, the speaker reflects on the value of calculus, highlighting its ability to solve real-world problems involving areas and instantaneous velocities. The speaker encourages viewers to explore calculus, despite its challenging nature, and appreciates its capacity to address complex issues. The video ends with the speaker promoting additional math resources and inviting viewers to engage with their content for further assistance.
Mindmap
Keywords
💡Calculus
💡Area
💡Integration
💡Derivative
💡Instantaneous Velocity
💡Formula
💡Rectangle
💡Estimate
💡Volume
💡Function
💡Infinity
Highlights
The video aims to demystify calculus and help viewers appreciate its value.
Calculus allows for finding the precise area of any shape, even those without a direct formula.
The concept of calculus can be introduced to sixth graders by relating it to the shapes they've learned, like circles, rectangles, and triangles.
To estimate the area under a squiggly curve, one can use rectangles to approximate the shape.
As the rectangles become thinner, the estimate of the area under the curve becomes more precise.
The ultimate thinnest rectangle would be infinitely small, leading to the precise area calculation.
Calculus notation involves the use of integrals to represent the sum of areas under a curve.
The area problem in calculus is also known as integration.
Calculus can solve for instantaneous velocity, which is the speed of an object at a precise moment in time.
Derivatives are a concept in calculus used to find instantaneous velocity and rates of change.
The video provides a real-world example of calculating the speed of a car at a specific time during acceleration.
Another example given is calculating the instantaneous velocity of a baseball falling from a building.
Calculus is not just about areas and velocities; it can solve a wide range of real-world problems.
The video encourages viewers to explore calculus despite its challenging nature.
The presenter, John, is the founder of Tablet Class Math and has experience teaching middle and high school math.
Links to math resources and courses are provided in the video description for further learning.
The video concludes with a call to action for viewers to engage with the content and pursue their mathematical education.
Transcripts
Browse More Related Video

Calculus: Why does integrating a function give area under its curve?
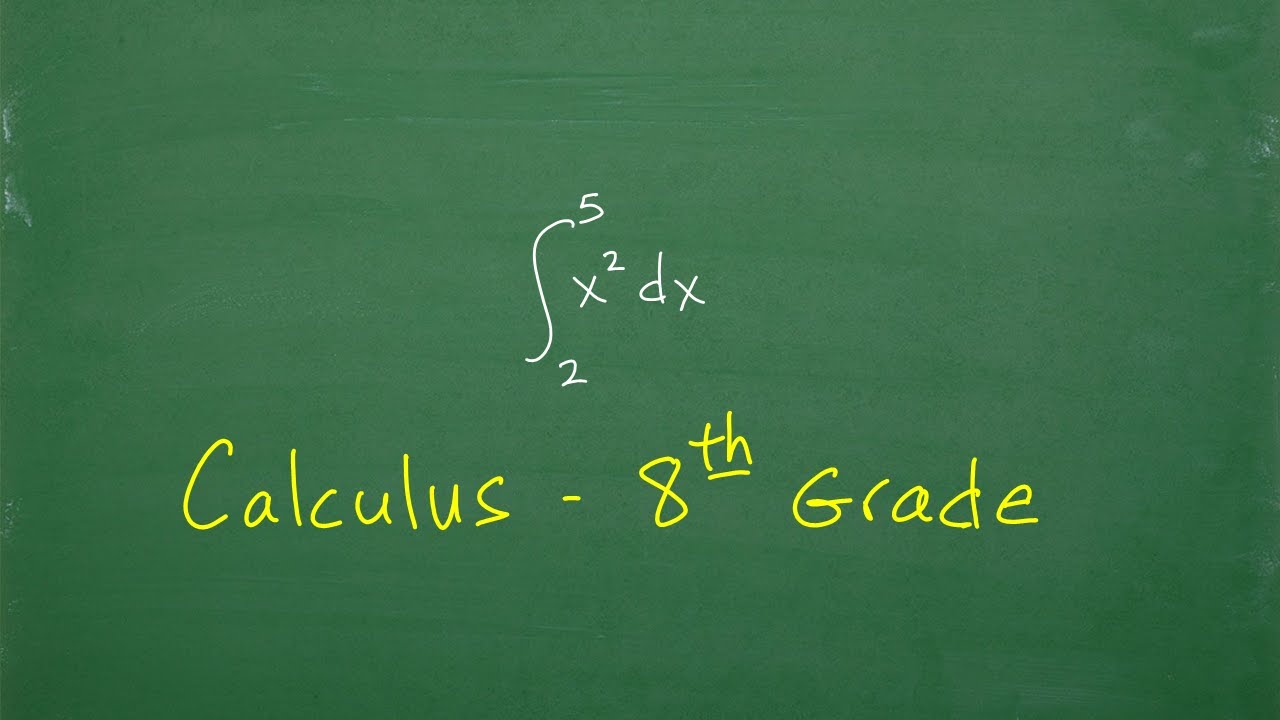
Calculus – taught at the 8th grade level
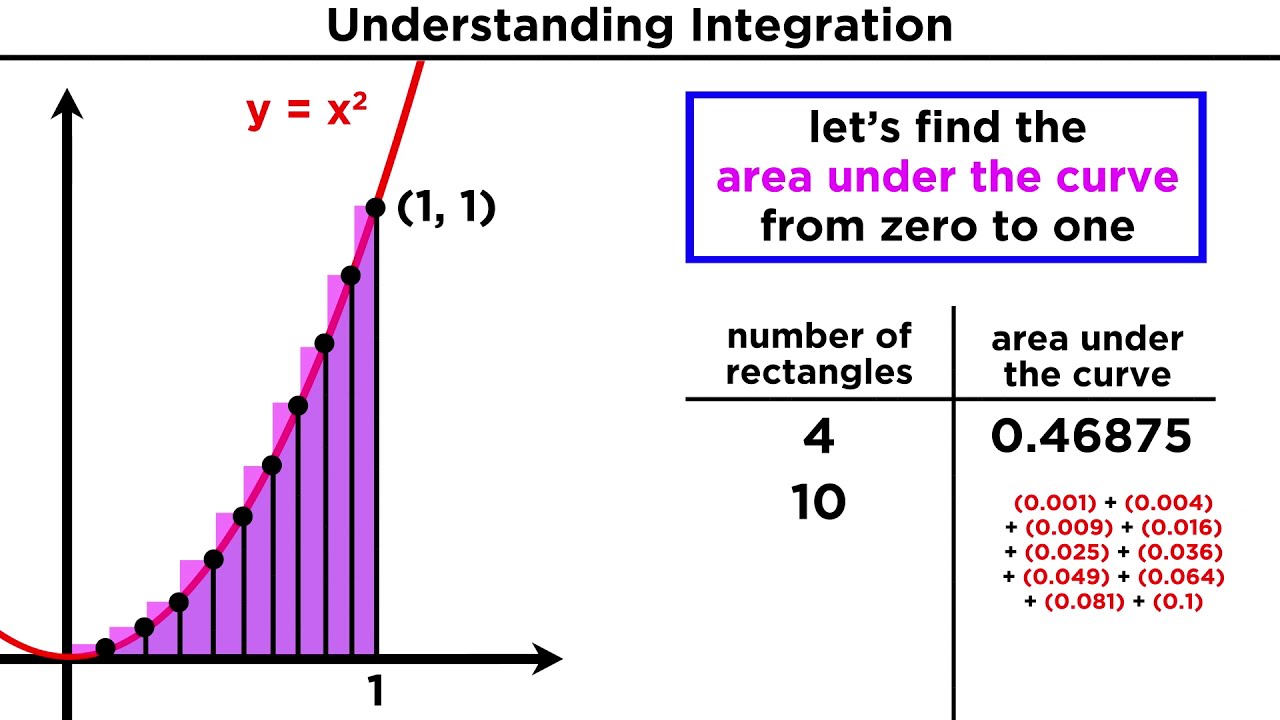
What is Integration? Finding the Area Under a Curve

Calculus explained through a story
01 - What Is an Integral in Calculus? Learn Calculus Integration and how to Solve Integrals.

Calculus, explained at a very BASIC level…
5.0 / 5 (0 votes)
Thanks for rating: