01 - What Is an Integral in Calculus? Learn Calculus Integration and how to Solve Integrals.
TLDRThis transcript introduces the concept of integration in calculus, emphasizing its practical applications in determining work done through force and distance. It explains how work, defined as force times distance, can be visually represented as the area under a force curve on a graph. The lesson then explores how to calculate work when force isn't constant, using the idea of approximating areas under curves with rectangles, and finally introduces the integral as a method to find the exact area under a curve by summing infinitesimally small rectangles. The integral's broader applications in science and engineering are also hinted at, motivating learners to understand its significance beyond mere academic interest.
Takeaways
- 📚 Integration in calculus is the process of calculating areas under curves, which is the opposite of differentiation.
- 🔄 The concept of integration is introduced through the analogy of work in physics, where work is defined as Force Times Distance.
- 🏗️ Work done (in physics) is represented graphically as the area under the force curve on a graph, which is a rectangle when force is constant.
- 📈 When force varies (non-constant), the work done is represented by the area under the curve, which requires integration to calculate.
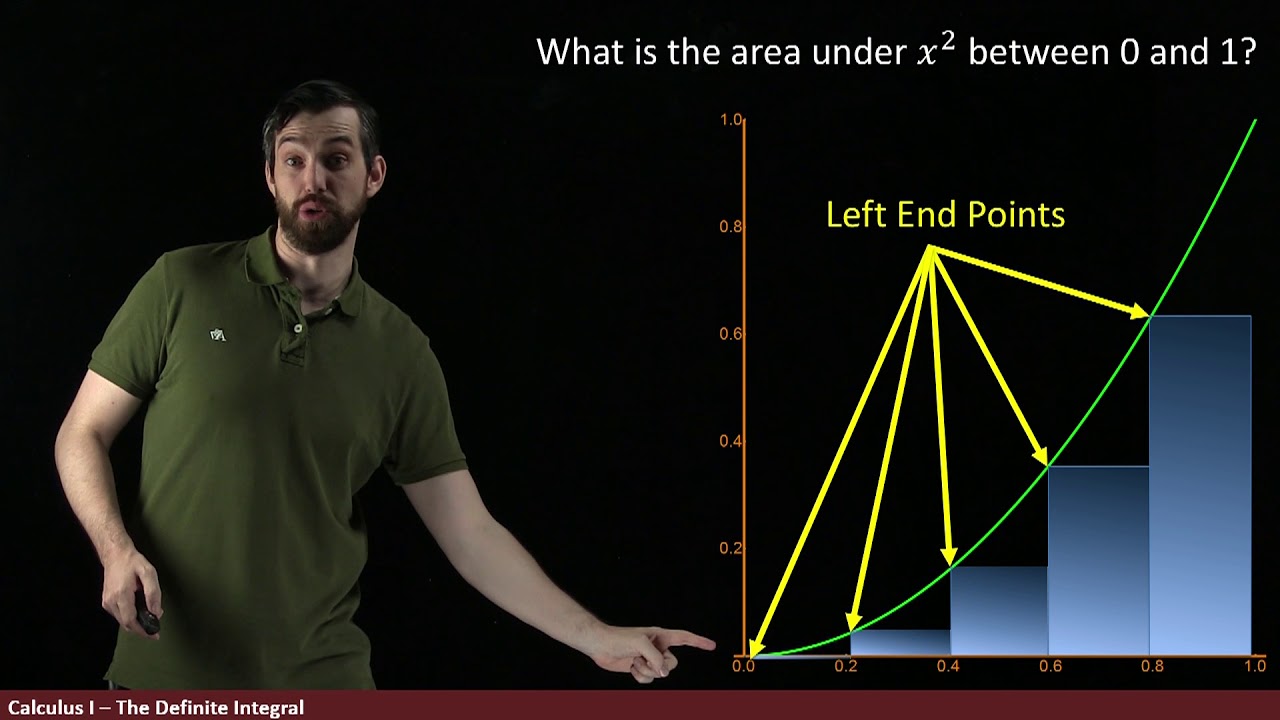
- 🔻 To approximate the area under a curve, rectangles can be used to 'sum up' the areas, with the rectangles becoming narrower to improve accuracy.
- 🎯 The limit of an infinite number of rectangles with width approaching zero (ΔX) is used to define the integral and find the exact area under the curve.
- 📊 The integral is represented by the summation symbol (∑) and involves adding up the product of the function value (f(X)) and an infinitesimally small width (ΔX).
- 🌐 Integrals have wide applications in science, engineering, and math, not just for calculating work, but also for summing up infinitesimally small quantities in various contexts.
- 🛠️ The process of integration involves finding the antiderivative of a function and applying the Fundamental Theorem of Calculus to evaluate the integral.
- 📚 The script emphasizes the importance of understanding the concept of integration and its applications beyond just the mathematical procedure.
- 🚀 The course aims to provide practice and techniques for calculating integrals, ensuring a deep understanding of the subject matter.
Q & A
What is the main focus of this lesson in the context of calculus?
-The main focus of this lesson is to provide an in-depth understanding of integration in calculus, specifically by practicing the calculation of integrals and explaining the concept through the application of work in physics.
How does the lesson connect calculus with physics?
-The lesson connects calculus with physics by using the concept of work, defined as Force Times Distance in physics, to illustrate the idea of integration. The work done is represented by the area under the force curve over a certain distance, which is a geometric representation that calculus can calculate using integration.
What is the relationship between derivatives and integrals in calculus?
-Derivatives and integrals are two fundamental concepts in calculus that are closely related. Derivatives deal with the rate of change of a function, while integrals are the opposite, essentially representing the accumulation of small quantities to find a larger value, such as the area under a curve.
How does the lesson introduce the concept of integration?
-The lesson introduces the concept of integration by first discussing the concept of work in physics and then showing how the work done can be represented as the area under a curve on a graph. It then explains that integration in calculus is used to calculate the area under such curves, even when they are not simple shapes like rectangles.
What is the significance of the area under a curve in the context of work in physics?
-In the context of work in physics, the area under a curve represents the total work done. When a constant force is applied over a distance, this area is a rectangle, and the work can be calculated directly as the product of the force and the distance. However, when the force varies, the work is represented by the more complex area under the curve, which requires integration to calculate.
How does the concept of limits play a role in the definition of an integral?
-The concept of limits is crucial in the definition of an integral. It involves taking the limit as the number of rectangles approaches infinity and the width of these rectangles (Δx) approaches zero. This process allows for an increasingly accurate approximation of the area under the curve, ultimately leading to the exact area when the limit is taken.
What is the practical application of integration discussed in the lesson?
-The practical application of integration discussed in the lesson is the calculation of work done on a moving object, which is represented by the area under a force curve. This concept is then extended to other applications such as calculating the total electric field along a path or determining the flow rate of a fluid through a pipe with varying speeds across its cross-section.
How does the lesson motivate the learning of integration?
-The lesson motivates the learning of integration by showing its direct application in physics for calculating work, and by extension, its broad utility in science, engineering, and math for adding up an infinite number of tiny quantities to find a larger value, such as areas or volumes.
What is the mathematical definition of work in the context of this lesson?
-In the context of this lesson, the mathematical definition of work is the product of the force applied and the distance moved by an object in the direction of the force. When the force is constant, work is calculated as Force Times Distance. When the force varies, work is represented by the area under the force curve from the initial to the final position.
What is the role of the summation in the process of approximating the area under a curve?
-The summation plays a crucial role in the process of approximating the area under a curve by adding up the areas of numerous thin rectangles that fit under the curve. Each rectangle's area is found by multiplying its width (Δx) by the height (the function value f(x) at that point). The summation helps in creating a closer approximation of the actual area under the curve.
Outlines
📚 Introduction to Integration in Calculus
This paragraph introduces the concept of integration within the broader scope of calculus. It emphasizes the importance of understanding derivatives before moving on to integration, as the two are closely related. The speaker encourages the audience to review material on derivatives if they are not confident in their understanding. The main idea is to prepare the audience for a deep dive into integration, stressing that understanding the concept is crucial for effective problem-solving in calculus.
📐 Work and Integration in Physics
The speaker connects the concept of work from physics to integration in calculus. By using the formula for work (Force times distance), the speaker explains how the area under a force curve on a graph represents work done. This analogy is used to transition into the idea of integration, which is essentially calculating the area under a curve. The paragraph aims to provide a practical understanding of integration by relating it to a familiar concept from physics.
📊 Visualizing Work with Force and Distance Graphs
This paragraph delves deeper into the visual representation of work using force-distance graphs. It explains how the area under a rectangle on such a graph, which represents constant force, equates to work done. The speaker then introduces a scenario where force is not constant, leading to a more complex curve. The challenge of calculating work in this case is introduced, setting the stage for the discussion of integration as a solution to finding the area under such curves.
🔢 Approximating Areas Under Curves
The speaker discusses the method of approximating the area under a curve when the force is not constant. By using the concept of rectangles to approximate the area, the speaker illustrates how increasing the number of rectangles and making them narrower can lead to a better approximation. The paragraph introduces the idea of using summation to add up the areas of these rectangles, which is a precursor to the formal definition of integration.
🌟 The Formal Definition of Integration
In this paragraph, the speaker provides the formal definition of integration. It explains that integration is the limit of the summation of rectangles' areas as the number of rectangles approaches infinity and their width approaches zero. The speaker uses the notation and concepts of calculus to describe the process of finding the exact area under a curve, which is the integral of a function.
🔄 Recap and Further Applications of Integration
The speaker recaps the concept of integration and its motivation derived from the concept of work in physics. It reiterates the process of approximating the area under a curve with rectangles and how refining these approximations leads to the definition of integration. The paragraph also extends the application of integration beyond work, mentioning its use in various scientific and engineering fields, such as calculating electric fields or fluid flow rates in pipes with varying cross-sections.
🎓 Encouragement for Future Learning
The speaker concludes by encouraging the audience to understand the motivation behind learning integration and to follow along in future lessons to master the calculation of integrals. The emphasis is on building skills through practice and understanding the terminology and concepts, promising that by the end of the course, the audience will be proficient in taking integrals in calculus.
Mindmap
Keywords
💡Calculus
💡Integration
💡Derivatives
💡Work (Physics)
💡Force
💡Area Under a Curve
💡Summation
💡Limit
💡Differential
💡Approximation
Highlights
Introduction to calculus and its two main topics: derivatives and integration.
Explanation of derivatives as the rate of change or the 'slope' of a function.
Integration as the opposite process of differentiation, dealing with accumulation of change.
The importance of understanding derivatives before moving on to integration.
Integration's real-world application in calculating work, defined as Force Times Distance in physics.
Graphical representation of work as the area under a force-distance curve.
Discussion on how work is calculated when force is not constant, relating it to the area under a curve.
Introduction to the concept of approximating areas under curves using rectangles.
The process of refining approximations by making rectangles narrower to better fit the curve.
The mathematical notation and process of summing areas of rectangles to approximate the area under a curve.
The definition of an integral as a limit of a summation of rectangles' areas as their width approaches zero.
Explanation of the integral symbol and its relation to summing infinitesimally small rectangles.
Motivation for learning integration through practical applications like calculating work.
Broader applications of integration in science, engineering, and other fields beyond physics.
The use of integration in calculating the flow rate in a pipe with varying speeds across its cross-section.
Emphasis on the importance of practice in mastering the skills of integration in calculus.
The course's aim to make learners experts at taking integrals in calculus through practice and understanding.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: