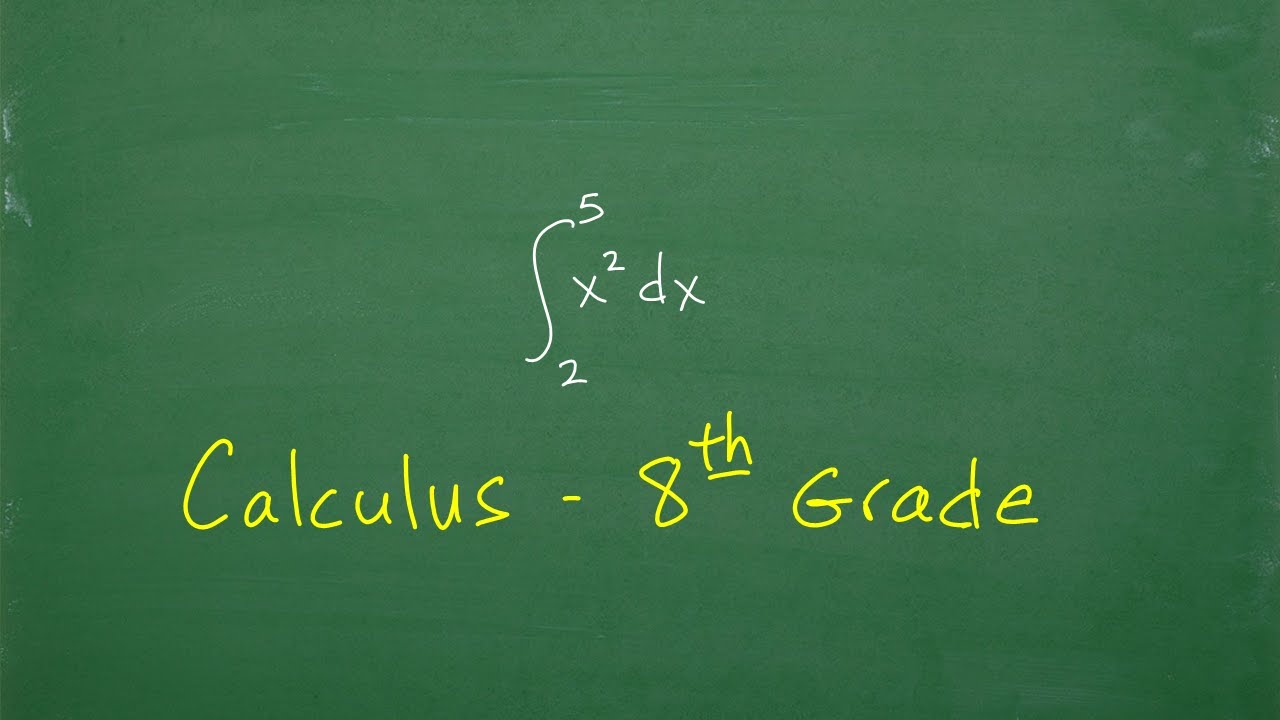Calculus, explained at a very BASIC level…
TLDRThis video script by John, a passionate math educator with decades of experience, aims to demystify calculus for beginners. John explains that calculus, often perceived as an advanced subject for professionals like engineers and scientists, is accessible to everyone with the right guidance. He introduces the fundamental concept of calculus, which is finding areas of complex shapes that don't have straightforward formulas. John uses the example of calculating the area under a curve, like a parabola, between two points on the x-axis, to illustrate the process of integration in calculus. By breaking down the problem into smaller, manageable rectangles and using calculus rules, he demonstrates that even complex problems can be solved with basic arithmetic. The script encourages viewers to approach calculus with curiosity and confidence, emphasizing that it's a powerful mathematical tool used widely in STEM fields.
Takeaways
- 📚 The video aims to demystify calculus and introduce basic concepts to viewers without a strong math background.
- 👨🏫 The presenter, John, is an experienced math teacher passionate about making math accessible to everyone.
- 🔗 John promotes his math help program at tcmathacademy.com for those interested in learning more about mathematics.
- 📉 The script provides a brief overview of the high school math curriculum leading up to calculus, typically taken in college for STEM majors.
- 🎯 Calculus is introduced as a tool primarily for finding areas and volumes of complex shapes that do not have straightforward formulas.
- 📏 The concept of 'integration' in calculus is explained as the process of adding up the areas of infinitesimally small rectangles to estimate the area under a curve.
- 📚 The script simplifies the process of integration by demonstrating how to find the area under a curve (y = x^2) from 2 to 3 on the x-axis.
- 📈 The presenter uses a step-by-step approach to show how to apply calculus rules to find the area, emphasizing that calculus has specific rules that can be learned.
- 📝 The final calculation involves integrating x^2 to get x^3/3, and then evaluating this from the bounds 2 to 3 to find the area.
- 🧮 The arithmetic involved in the final calculation is basic, demonstrating that understanding calculus concepts can be more approachable than the symbols suggest.
- 🌐 The video concludes by emphasizing that calculus is a powerful mathematical language used widely in engineering, technology, and other fields, and encourages viewers to learn it.
Q & A
What is the main purpose of the video?
-The main purpose of the video is to introduce and explain basic concepts of calculus to viewers who may not have a strong math background.
Who is the instructor in the video?
-The instructor in the video is John, who has been teaching middle and high school math for decades.
What is the website mentioned in the video for learning math?
-The website mentioned in the video for learning math is tcmathacademy.com.
Why is calculus important for certain college majors?
-Calculus is important for college majors in STEM fields (science, technology, engineering, and mathematics) as well as finance and economics because it is used to solve complex problems related to area, volume, and other mathematical concepts.
What is the first concept of calculus introduced in the video?
-The first concept of calculus introduced in the video is the ability to find the area of various shapes, including those without a straightforward formula.
What does the instructor suggest for estimating the area under a curve?
-The instructor suggests using rectangles to estimate the area under a curve by breaking the area into smaller, more manageable parts, and then refining the estimate by using skinnier rectangles to get closer to the actual area.
What is the process called that allows us to find the area under a curve using calculus?
-The process is called integration, and it involves adding up the areas of infinitely small rectangles (or strips) under the curve.
What is the specific shape that the instructor is trying to find the area under in the video?
-The specific shape the instructor is trying to find the area under is a part of a parabola defined by the equation y = x^2, bounded by the x-axis and the vertical lines x = 2 and x = 3.
What is the calculus notation used to represent the process of finding the area under a curve?
-The calculus notation used to represent the process of finding the area under a curve is the integral symbol, often represented as an elongated 'S'.
What is the rule used in the video to integrate x^2 and find the area under the curve?
-The rule used to integrate x^2 is to add 1 to the exponent, resulting in x^3, and then divide by the new exponent, which in this case gives x^3/3.
How does the instructor calculate the area under the curve y = x^2 from x = 2 to x = 3?
-The instructor calculates the area by evaluating the integral of x^2 from x = 2 to x = 3, which results in (3^3/3) - (2^3/3), simplifying to 19/3 or approximately 6.3 square units.
What analogy does the instructor use to explain the complexity of calculus?
-The instructor uses the analogy of learning a new language, such as Spanish or Chinese, to explain that calculus is a mathematical language that may seem difficult at first but can be understood with practice and familiarity.
What advice does the instructor give for those who are interested in learning calculus?
-The instructor advises those interested in learning calculus not to be intimidated by the symbols and to approach it as a language to be learned, emphasizing that with interest and effort, anyone can learn calculus.
Outlines
📚 Introduction to Calculus
The speaker, John, introduces the topic of calculus, aiming to simplify its perception as an advanced and intimidating subject. He clarifies that while calculus is often associated with rocket scientists and engineers, it's not inherently inaccessible. John, an experienced math teacher, assures viewers with little to no math background that they can understand the basics of calculus. He promotes his math help program and invites viewers to share their initial thoughts on calculus in the comments.
📘 When and Who Should Study Calculus
John outlines the typical high school math curriculum, explaining that calculus is usually taken in college by students pursuing STEM fields—science, technology, engineering, and mathematics. He emphasizes that calculus is essential for those planning to become computer scientists, chemists, engineers, or mathematicians. John also mentions that finance and economics majors might need to study calculus. He encourages viewers that with the right preparation, anyone can learn calculus.
📙 Calculus and the Concept of Area
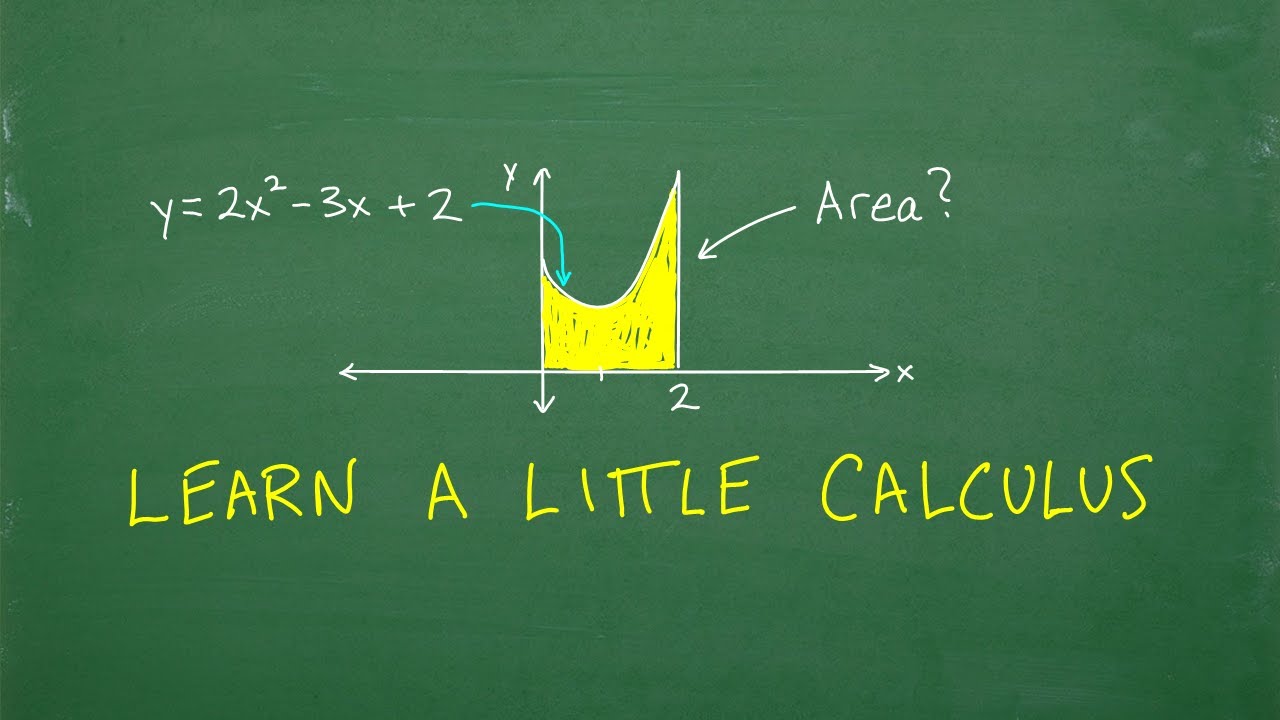
The script shifts focus to the practical applications of calculus, starting with the concept of area. John explains that while the area of basic shapes like rectangles, circles, and triangles can be easily calculated using standard formulas, calculus is needed to find the area of more complex shapes without straightforward formulas. He introduces the idea of using calculus to estimate and calculate areas of irregular shapes encountered in real-life situations.
📒 The Process of Integration in Calculus
John delves into the concept of integration, a fundamental operation in calculus, which involves summing up infinitesimally small rectangles to approximate the area under a curve. He illustrates how using smaller and smaller rectangles can improve the accuracy of the area estimation. The process is likened to adding up the areas of these tiny rectangles to get closer to the actual area under the curve, which calculus can precisely determine.
📔 Applying Calculus to Define a Shape and Calculate Its Area
The speaker provides a step-by-step guide on how to use calculus to define a specific shape under a curve and calculate its area. He uses the example of a parabola, y = x^2, bounded by the x-axis and specific vertical lines from x=2 to x=3. John introduces calculus notation, explaining the integral symbol and how it's used to find the area under the curve within the given bounds. He emphasizes that understanding the basics of calculus allows for the calculation of areas that would otherwise be impossible to determine.
📕 Calculating the Area Under a Curve Using Integration
John demonstrates the process of integrating x^2 from 2 to 3 to find the area under the curve. He simplifies the calculus rule, showing that the integral of x^2 is x^3/3. By applying this rule, he guides viewers through the calculation, emphasizing that the arithmetic involved is not overly complex. The final result is an approximation of the area, which John calculates to be about 6.3 square units, thereby successfully applying calculus to solve a real-world problem.
📖 Embracing Calculus as a Universal Mathematical Language
In the concluding paragraph, John reflects on the nature of calculus as a mathematical language that, like any other language, may seem daunting at first but becomes comprehensible with understanding. He encourages viewers not to be intimidated by the symbols and concepts of calculus, asserting that with interest and effort, anyone can learn it. John highlights the ubiquity of calculus in modern engineering and technology, advocating for its study due to its power and wide-ranging applications.
Mindmap
Keywords
💡Calculus
💡STEM
💡Area
💡Integration
💡Rectangle
💡Parabola
💡Function
💡Algebra
💡Estimation
💡Differentiation
Highlights
Introduction to the basics of calculus without advanced math prerequisites.
Calculus is often associated with rocket scientists and engineers, but it's accessible to everyone.
The presenter, John, has decades of experience teaching middle and high school math.
High school math curriculum typically includes algebra, geometry, algebra 2, and pre-calculus.
STEM fields require calculus for advanced study in college.
Calculus is essential for majors like computer science, chemistry, engineering, and mathematics.
Calculus is used to find areas of complex shapes without a standard formula.
The concept of breaking complex areas into smaller, manageable rectangles to estimate total area.
Integration in calculus allows for the calculation of areas under curves.
The process of finding the area under a curve using infinitely small rectangles.
Defining a shape by its boundaries and a rule for the curve.
Using algebra to describe a curve with an equation, such as y = x^2 for a parabola.
Calculating the area under a curve between specific bounds using calculus.
The integral notation and process in calculus to find the area under the curve.
A simplified rule for integrating x^n is to add 1 to the exponent and divide by the new exponent.
Practical demonstration of calculating the exact area under a curve using calculus.
Calculus as a mathematical language that can be learned with interest and practice.
Encouragement for viewers to learn calculus due to its wide applications and power.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: