Calculus explained through a story
TLDRIn this engaging video script, the story of Bob, a resident of a snowy mountain hut, serves as an allegory for the fundamental concepts of calculus. When a tree falls and a bridge section breaks, Bob faces the challenge of crossing the bridge to check on his beloved deer friends in the meadow below. He ingeniously uses a fallen tree to create a makeshift ramp, which introduces the concept of differentiation – finding the slope of a curve at a specific point. Upon reaching the meadow, Bob grapples with the problem of calculating the area of the fallen bridge, an irregular shape, to determine if it has deprived the deer of their food source. He uses pebbles and eventually sand grains to approximate the area, illustrating the concept of integration – finding the area under a curve by breaking it into infinitesimally small pieces. Through Bob's meticulous efforts, he ensures the deer will have enough grass, and the video concludes with a clear explanation of how these everyday actions relate to the mathematical principles of calculus.
Takeaways
- 📚 **Storytelling in Mathematics**: The video uses a narrative approach to explain complex mathematical concepts, making them more accessible and relatable.
- ⛰️ **Setting the Scene**: The story is set in a mountainous region, which provides a context for the problems that Bob, the protagonist, must solve.
- 🌳 **Environmental Impact**: A tree falls and a bridge section breaks, highlighting the impact of natural events on the environment and Bob's immediate surroundings.
- 🔍 **Problem Solving**: Bob's actions demonstrate problem-solving skills, as he must find a way to cross the broken bridge and ensure the safety of the deer in the meadow.
- 🧭 **Differentiation**: The concept of differentiation is introduced through Bob's attempt to measure the steepness of a makeshift ramp using a pebble as a unit of measurement.
- 📐 **Slope of a Curve**: Bob calculates the slope at a specific point on a curve (the bridge) by treating a small section as a straight line, which is a fundamental idea in calculus.
- 🦌 **Concern for Wildlife**: Bob's concern for the deer's well-being and their food supply brings an ethical dimension to the story, emphasizing the importance of considering the impact of our actions on nature.
- 🌱 **Integration through Area Calculation**: Bob's method of approximating the area covered by the fallen bridge using pebbles and eventually sand grains illustrates the concept of integration.
- ⏳ **Accuracy and Precision**: The story emphasizes the importance of accuracy in calculations, as Bob seeks to ensure the deer have enough grass to survive, reflecting the precision required in mathematical analysis.
- 🔬 **Practical Application of Math**: The script shows how mathematical principles like differentiation and integration can be applied to real-world scenarios, such as measuring slopes and areas.
- 🎓 **Educational Content**: The video is educational, aiming to teach viewers about calculus through an engaging story, rather than complex formulas or equations.
Q & A
What is the main theme of the story presented by Toby?
-The main theme of the story is to illustrate the concepts of calculus, specifically differentiation and integration, through a narrative about a character named Bob and his experiences in the mountains.
Who is the character in the story and where does he live?
-The character in the story is a man named Bob, who lives in a small hut in the snowy mountains.
What problem does Bob encounter with the bridge?
-Bob encounters a problem with the bridge because a section of it, made of logs, breaks away and falls, leaving only a couple of wires holding the logs together.
How does Bob plan to cross the bridge with the missing section?
-Bob plans to use a fallen tree to create a ramp across the wires that were left in place on the bridge, allowing him to walk down and cross over.
What does Bob use to measure the steepness of the makeshift ramp?
-Bob uses a pebble as a measuring stick to estimate how many pebbles would fit vertically and horizontally between the missing logs to determine the steepness of the ramp.
What mathematical concept does the act of Bob using the pebble to measure the slope represent?
-The act of using the pebble to measure the slope represents the concept of differentiation in calculus, where the slope of a curve at a particular point is determined by examining a small segment of the curve.
What does Bob notice about the deer in the meadow after the bridge section falls?
-Bob notices that all the deer are alive and not hurt by the fallen bridge section, but he becomes concerned about the grass in the meadow being covered by the bridge, potentially affecting the deer's food supply.
How does Bob attempt to measure the area covered by the fallen bridge in the meadow?
-Initially, Bob uses pebbles to approximate the area covered by the fallen bridge. Later, he refines his measurement by using individual grains of sand to get a more accurate approximation of the area.
What mathematical concept is illustrated by Bob's method of using sand grains to measure the area?
-The method of using sand grains to measure the area illustrates the concept of integration in calculus, which involves finding the area under a curve by summing up an infinite number of infinitesimally small rectangles.
What is the conclusion Bob reaches after calculating the area of the fallen bridge section in the meadow?
-After calculating the area, Bob concludes that even with the grass covered by the fallen bridge section, there is still enough grass in the meadow to feed the deer.
What does the story of Bob and the bridge teach us about the practical applications of calculus?
-The story teaches us that calculus, through concepts like differentiation and integration, can be used to solve real-world problems, such as determining the slope of a ramp or the area covered by an irregular shape.
Why does the story emphasize Bob's concern for the deer and his dedication to accurately measure the area?
-The emphasis on Bob's concern and dedication highlights the importance of precision and accuracy in mathematical calculations, especially when the outcomes can significantly affect real-life situations, such as the well-being of the deer.
Outlines
🌲 Bob's Mountain Adventure Begins
In this opening paragraph, Toby introduces the story without any mathematical formulas or equations. The narrative focuses on Bob, a character living in a mountain hut during a stormy day. A tree and part of a bridge are blown over, which Bob needs to address. The story is set to reveal the intuition behind calculus through Bob's actions. Bob is concerned about the well-being of deer in a meadow and plans to use a fallen tree to create a ramp across the broken bridge. The key challenge is ensuring the ramp is not too steep for him to climb with his worn-out shoes.
🛠️ Bob Measures the Bridge's Slope
Bob uses a pebble as a makeshift measuring tool to determine the steepness of the bridge ramp he plans to create. He estimates that three pebbles can fit both vertically and horizontally in the gap of the broken bridge. This suggests that the slope of the bridge is as tall as it is wide, which is manageable for Bob. The paragraph illustrates the concept of differentiation in mathematics, where a curved line (the bridge) is analyzed at a specific point, treating it as a straight line to find the slope.
🌱 Bob's Concern for the Deer's Food Supply
After safely crossing the bridge, Bob discovers that the fallen bridge section is covering the grass in the meadow, which could potentially lead to a shortage of food for the deer. Bob knows the amount of grass a deer consumes in a season and the original amount of grass in the rectangular meadow. He faces the challenge of calculating the area covered by the fallen bridge to determine if there is enough grass left for the deer. Initially, he tries to approximate the area with pebbles, but acknowledges the inaccuracy of this method.
⏳ Bob's Quest for Accurate Measurement
Determined to find an accurate measurement of the area covered by the fallen bridge, Bob decides to use individual grains of sand from the riverbed. By placing grains of sand in columns along the shape, he meticulously counts them to find the area. This process is time-consuming, stretching over two days and nights. Bob's dedication to the task reflects his concern for the deer's well-being. The act of using countless small elements (sand grains) to measure an area exemplifies the concept of integration in calculus, where an area is determined by summing infinitely small parts.
Mindmap
Keywords
💡Calculus
💡Differentiation
💡Integration
💡Slope
💡Friction
💡Measuring
💡Approximation
💡Area
💡Deer
💡Mountains
💡Ramp
Highlights
Toby introduces a story to convey the intuition behind calculus without using mathematical formulas.
The story is set in a mountainous region during a windy and stormy day.
A tree falls and a section of a log bridge breaks, leaving only wires.
Bob, a character in the story, is concerned for the well-being of deer in a meadow below.
Bob plans to use a fallen tree as a ramp to cross the broken bridge.
Bob uses a pebble to measure the steepness of the ramp, relating it to his ability to climb.
The story illustrates the concept of differentiation by finding the slope of a curve at a point.
Bob discovers that the deer are safe, but he is concerned about the grass being covered by the fallen bridge.
Bob calculates the area of the fallen bridge to determine its impact on the available grass for the deer.
He approximates the irregular shape of the fallen bridge using pebbles and later sand for more accuracy.
The process of using smaller and smaller elements to approximate an area exemplifies integration.
Bob's dedication to accuracy in measuring the area reflects the mathematical concept of finding the area under a curve.
After a meticulous count of sand grains, Bob concludes that there is enough grass for the deer.
The story concludes with Bob's relief and the viewer's understanding of calculus concepts through a practical scenario.
Toby invites viewers to subscribe for more content that makes mathematics accessible and engaging.
The narrative approach used in the story effectively teaches calculus principles without complex equations.
The story highlights the practical applications of calculus in everyday scenarios, making it more relatable.
Transcripts
Browse More Related Video

How I would explain Calculus to a 6th grader
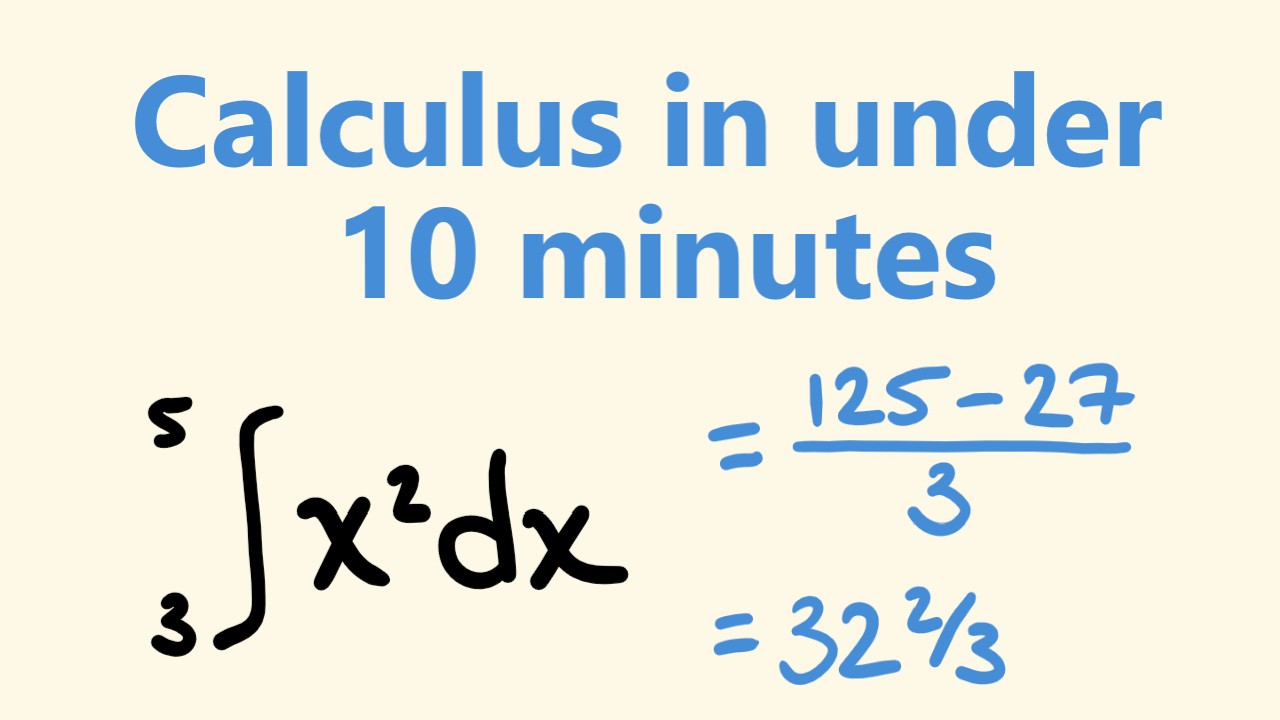
How to do Calculus in Under 10 Minutes

Calculus, explained at a very BASIC level…
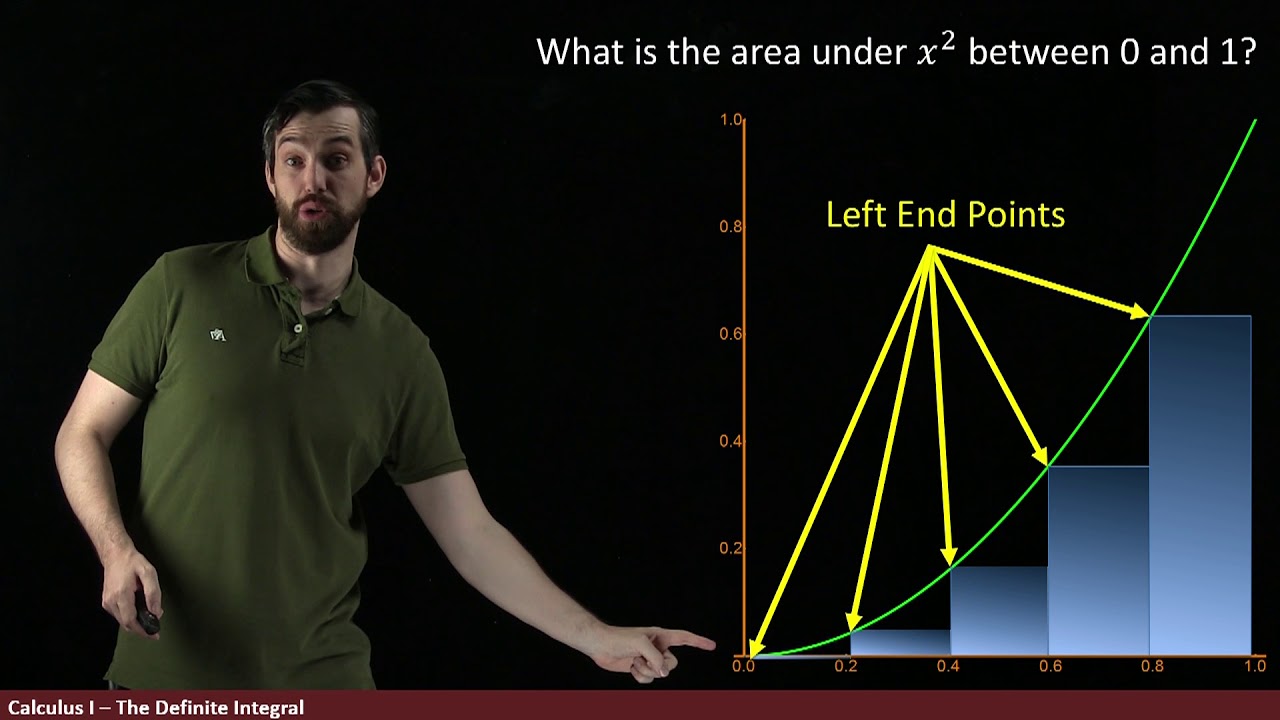
The Definite Integral Part I: Approximating Areas with rectangles

Defining Double Integration with Riemann Sums | Volume under a Surface

Why Are Slope and Area Opposite: The Fundamental Theorem of Calculus
5.0 / 5 (0 votes)
Thanks for rating: