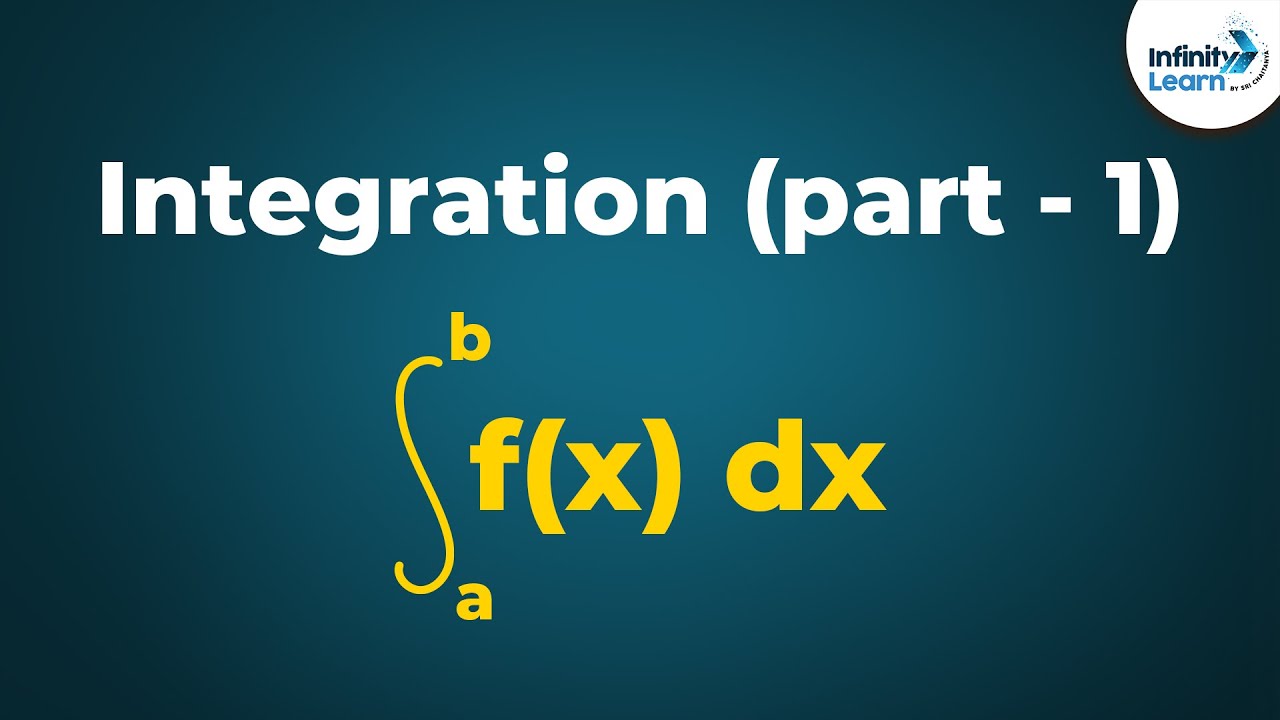Calculus: Why does integrating a function give area under its curve?
TLDRThe video script delves into the concept of integration in mathematics, explaining why integrating a function results in the area under a curve. The presenter shares both a traditional method of understanding integration as the summation of infinitesimally small rectangles and an alternative intuitive approach using the concept of limits and derivatives. By illustrating how the area under a curve can be approximated by rectangles and then showing how the limit process refines this approximation, the script effectively conveys the fundamental principle that integration is essentially finding the antiderivative, which can be used to calculate areas between specified bounds on the x-axis.
Takeaways
- 📈 The concept of integration is introduced as a way to find the area under a curve.
- 🏠 The basic definition of integration involves summing up infinitesimally small rectangles under the curve.
- 🔄 The symbol for integral (∫) is derived from the letter 'S' which stands for 'sum'.
- 📊 An alternative perspective on integration is presented, using the idea of a function that gives the area under the curve.
- 🤔 The video explores why integrating a function between two bounds gives us an area by considering the addition and subtraction of areas.
- 🔎 By zooming in on a strip of the curve, the video demonstrates how the area can be approximated by the product of the function's value and a small distance (height).
- 📐 The concept of limits is used to refine the approximation, leading to the definition of the derivative as the limit of the ratio of the area to the width as the width approaches zero.
- 🌟 The derivative is shown to be the key to understanding the relationship between the function and the area under the curve.
- 🧠 The video emphasizes the intuitive nature of this method, suggesting it's a more accessible way to understand integration compared to the traditional rectangle method.
- 📈 The integral of a function with respect to X is identified as the area function, which can be used to calculate areas between specific points by plugging in values.
- 🙏 The video concludes by encouraging viewers to like, share, and subscribe for more educational content on similar topics.
Q & A
What is the main topic of the video?
-The main topic of the video is explaining why integrating a function gives us the area under a curve.
How does the basic definition of integration relate to the area under a curve?
-The basic definition of integration involves adding up an infinite number of little rectangles under a curve, which approximates the area under the curve.
What is the symbol used to represent integration?
-The symbol used to represent integration is an elongated 'S', which stands for 'sum', indicating the summation of the infinite number of rectangles.
How does the video introduce an alternative way of thinking about integration?
-The video introduces an alternative way by considering the area under a curve as a function of 'a(x)' and showing how the difference in this function at points 'x' and 'x+h' can be used to derive the integral.
What does the video mean by 'extending the area function to a small distance H'?
-The video means that by extending the area function, we can consider the change in area (∆A) when the interval 'x' is increased by a small distance 'h', which helps in understanding the relationship between the function and the area under the curve.
How does the video use the concept of limits to explain integration?
-The video uses the concept of limits by taking 'h' to approach zero, which allows the expression to represent the instantaneous rate of change of the area function, leading to the understanding that integration of a function gives the area function.
What does the video imply about the relationship between the derivative and integration?
-The video implies that the derivative and integration are inverse operations. The derivative gives the rate of change of an area function, while integration undoes this operation to find the original area function.
How does the video suggest using integration to find the area between specific points?
-The video suggests that by integrating a function with respect to 'x', we obtain the area function. By evaluating this area function at specific points 'a' and 'b', we can find the area under the curve between these points.
What is the significance of the method explained in the video for understanding integration?
-The method explained in the video provides an intuitive understanding of integration by directly relating it to the concept of area under a curve and showing how it can be derived from the rate of change of this area.
How does the video compare the rectangle method to the method it introduces?
-The video suggests that while the rectangle method is a valid approach, the method it introduces offers a more intuitive understanding of the relationship between integration and the area under a curve.
Outlines
📚 Introduction to the Concept of Integration and Area Under a Curve
The speaker begins by expressing gratitude for the viewers' support and introduces the topic of integration. They explain that the video will delve into why integrating a function results in the area under a curve. The speaker shares their initial understanding of integration as summing up infinitesimally small rectangles under a curve, represented by the integral symbol. They also mention an alternative perspective they learned, which they find intriguing and wish to share with the audience. The explanation starts with a basic function on an X-Y graph, aiming to calculate the area under the curve from point 0 to X.
🔍 Deep Dive into the Relationship Between Integration and Area Calculation
The speaker continues the discussion by introducing a hypothetical function that calculates the area under the curve. They visualize the scenario of extending the area by a small distance H and explain how the area of the new blue strip can be expressed. The speaker then zooms in on the strip and explains the relationship between the height of the rectangle (f of x) and the area. They further explore the concept by considering the height at point X plus H, leading to an inequality that describes the error in the approximation of the area. The speaker simplifies this inequality by applying limits, ultimately demonstrating that the derivative of the area function is less than or equal to the function itself. This leads to the conclusion that integrating a function yields the area function, and by plugging in specific values, one can calculate the area between given points. The speaker emphasizes the intuitive nature of this method compared to the traditional rectangle method.
Mindmap
Keywords
💡Integrating
💡Area under a curve
💡Summation
💡Integral
💡Rectangle method
💡Limits
💡Derivative
💡First principles
💡Antiderivative
💡Rate of change
💡Fundamental theorem of calculus
Highlights
Integrating a function gives us the area under a curve, a concept that has been historically taught through the method of summing up small rectangles.
The traditional explanation uses the idea of summing rectangles under a curve, represented by the integral symbol, which is a stretched out 'S' for 'sum'.
An alternative perspective on integration involves considering the area under a curve as a function itself, which can be determined by inputting an 'x' value.
To understand integration, the concept of extending a curve to a small distance 'H' is introduced, allowing for the calculation of the area up to that point.
The area of a small strip under the curve can be represented by the function 'a', which changes as 'x' is replaced with 'x + H'.
The expression for the strip's area is derived by subtracting the smaller area (f(X+H) - f(X)) from the larger area (f(X+H)), resulting in f(X) * H.
As 'H' approaches zero, the area of the strip becomes more accurate, leading to a better approximation of the actual area under the curve.
The process of taking the limit as 'H' approaches zero results in the first principles of calculus, specifically the relationship between integration and differentiation.
The derivative of the area function with respect to 'X' is found to be less than or equal to 'f(x)', and by applying the limit, 'f(x)' becomes equal to the derivative of 'a'.
The integral of a function with respect to 'X' results in the area function, which can be used to calculate the area between specific points when certain values are plugged in.
This alternative method of understanding integration provides a more intuitive way of thinking about the area under curves and the relationship between integrals and derivatives.
The video presents a new way of thinking about integration that is more visual and intuitive, potentially making it easier for learners to grasp the concept.
The explanation connects the abstract concepts of calculus to a tangible visual representation, which can aid in the understanding and retention of the material.
The video emphasizes the importance of understanding the fundamentals of calculus, such as the relationship between integration and differentiation, to build a strong foundation in mathematics.
The method presented in the video can be seen as a bridge between the traditional 'rectangle method' of integration and the more advanced concepts of calculus.
The video encourages viewers to explore different methods of learning and understanding mathematical concepts, highlighting the value of diverse approaches in education.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: