Work, Energy, and Power - Basic Introduction

The Organic Chemistry Tutor

5 Apr 202161:44

EducationalLearning

32 Likes 10 Comments

TLDRThis video delves into the concepts of work, energy, and power, explaining their interrelations and significance in physics. Work is defined as the product of force and displacement, with the angle between these vectors affecting the work done. Energy, particularly kinetic and potential, is the capacity to do work, with kinetic energy linked to motion and potential energy to an object's position or condition. Power is introduced as the rate of doing work or energy transfer. The video uses examples like a ball colliding with a block and objects under gravitational influence to illustrate these principles, highlighting the conservation of mechanical energy in systems with only conservative forces like gravity.

Takeaways

🏋️ Work is accomplished by the action of a force causing a displacement, calculated as the product of the force and displacement.
🔄 Kinetic energy is the energy of motion, given by the formula KE = 0.5 * m * v^2, where m is mass and v is velocity.
🌐 Potential energy is stored energy, like gravitational potential energy (PE = m * g * h), based on an object's position or condition.
💥 Collisions involve the transfer of energy, where kinetic energy can convert to potential energy and vice versa.
📈 The work-energy theorem states that the net work done on an object equals the change in its kinetic energy.
⏱️ Power is the rate at which work is done or energy is transferred, calculated as power = work / time or force * velocity.
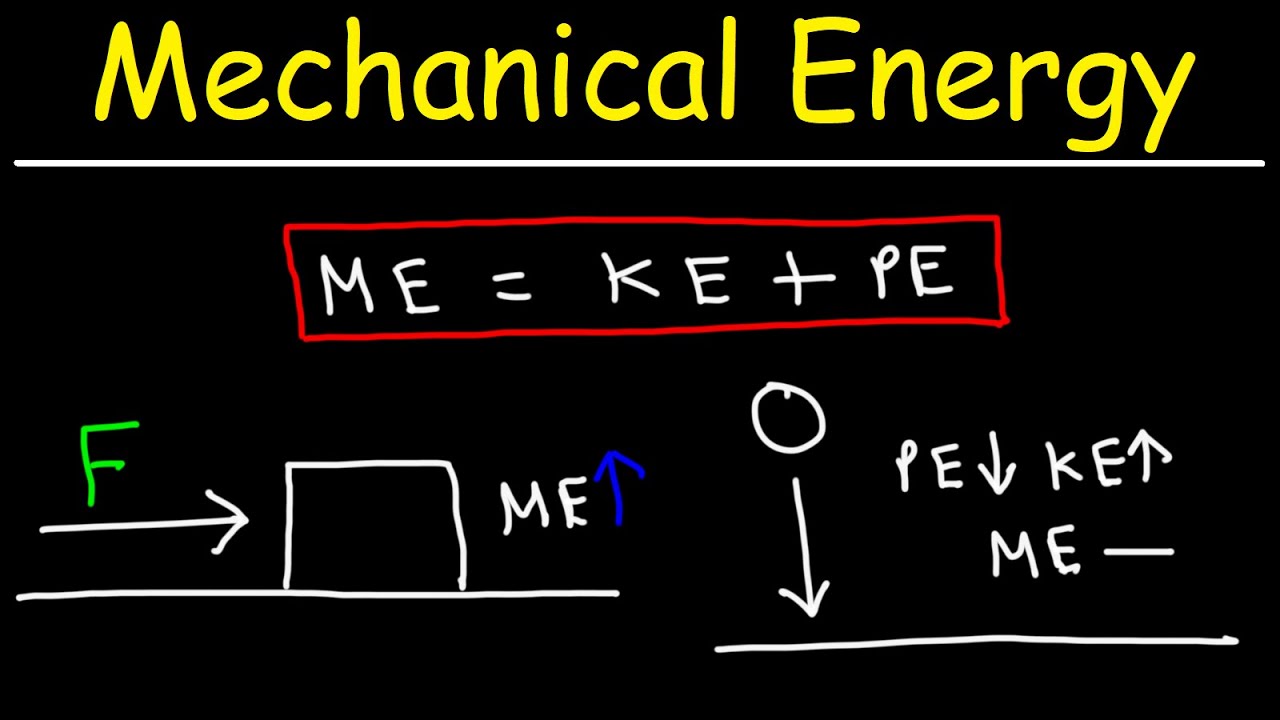
🔄 Mechanical energy is the sum of kinetic and potential energy, conserved when only conservative forces like gravity are acting on an object.
📉 Negative work means a force is doing work against the motion of an object, decreasing its kinetic energy.
📈 Positive work indicates a force is aiding the motion of an object, increasing its kinetic energy.
🔄 Non-conservative forces like friction do not conserve mechanical energy and can cause a net loss in the system's energy.
📊 The direction of force and displacement vectors determines the sign of work done: parallel vectors result in positive work, while anti-parallel vectors result in negative work.

Q & A

What is the definition of work in physics?
-In physics, work is the product of the force applied to an object and the displacement of the object in the direction of the force. It is accomplished when a force causes a displacement and is measured in joules.
How is the work done by a force related to the angle between the force and displacement vectors?
-The work done by a force is related to the angle between the force and displacement vectors through the cosine of the angle. If the force and displacement are in the same direction, the work is positive and maximum. If they are in opposite directions, the work is negative, and if they are perpendicular, the force does no work.
What are the two main forms of energy discussed in the script?
-The two main forms of energy discussed are kinetic energy, which is the energy of motion, and potential energy, which is stored energy that can be converted into other forms, such as kinetic energy.
How is kinetic energy calculated?
-Kinetic energy is calculated using the formula KE = 0.5 * m * v^2, where m is the mass of the object in kilograms and v is its velocity in meters per second.
What is the formula for calculating gravitational potential energy?
-Gravitational potential energy is calculated using the formula PE = m * g * h, where m is the mass in kilograms, g is the acceleration due to gravity (approximately 9.8 m/s^2), and h is the height in meters.
How does the work-energy theorem relate to the work done by a force on an object?
-The work-energy theorem states that the work done by a force on an object is equal to the change in the object's kinetic energy. If the force does positive work, the object's kinetic energy increases; if it does negative work, the kinetic energy decreases.
What happens to the mechanical energy of a system when only conservative forces are acting on it?
-When only conservative forces, such as gravity, are acting on a system, the mechanical energy (the sum of kinetic and potential energy) is conserved. It remains constant throughout the process.
How is power defined and how is it related to work?
-Power is defined as the rate at which work is done or energy is transferred. It is related to work through the formula P = W/t, where P is power, W is work done, and t is the time taken to do the work. Power is typically measured in watts, where 1 watt equals 1 joule per second.
What is the relationship between force, displacement, and work in the context of a constant force?
-In the context of a constant force, the work done is directly proportional to the product of the force and the displacement in the direction of the force. The greater the force or the longer the displacement, the more work is done.
How can you determine if a force is doing positive or negative work?
-A force is doing positive work if the angle between the force and displacement vectors is less than 180 degrees, and negative work if the angle is greater than 180 degrees. Perpendicular vectors (90 degrees) result in no work being done.
What is the significance of mechanical energy conservation in physics?
-The conservation of mechanical energy is significant because it is a fundamental principle that helps in understanding and predicting the behavior of systems where only conservative forces are at play. It simplifies the analysis of problems by allowing us to focus on the initial and final states without needing to consider the details of the intermediate processes.

Outlines

00:00

🔧 Understanding Work, Energy, and Power

This segment introduces the concepts of work, energy, and power in physics, explaining how they relate to each other. Work is described as the product of force and displacement, factoring in the direction through the cosine of the angle between force and displacement vectors. Energy is the capacity to do work, with kinetic energy associated with motion and potential energy representing stored energy due to position. The equations for calculating kinetic and gravitational potential energy are provided. The section emphasizes the different forms of potential energy and how energy transfer involves work.

05:01

⚖️ The Work-Energy Theorem and Conservation of Energy

This part delves into the interaction between a moving ball and a stationary block, illustrating Newton's third law and the work-energy theorem. It explains how forces between objects result in energy transfer and work done, either increasing or decreasing an object's kinetic energy. The discussion extends to the effects of force direction on work done and introduces the concept of net work as related to the change in kinetic energy, leading to a deeper understanding of energy conservation during motion and collision.

10:06

🔄 Gravity's Influence on Work and Energy

Focusing on the role of gravity, this section explores how gravitational forces do work, affecting kinetic and potential energy of moving objects. Through examples of a ball thrown upwards and another falling, it clarifies the concept of positive and negative work and its impact on kinetic energy. The narrative elucidates the interplay between gravitational potential energy and kinetic energy, demonstrating energy conservation and the concept of mechanical energy as the sum of kinetic and potential energy.

15:11

🚀 Potential Energy Variations and Non-Conservative Forces

This part examines the behavior of objects under different forces, explaining how potential energy varies with position and how non-conservative forces like friction and applied forces affect mechanical energy. It specifically discusses how applying a force can simultaneously increase an object's kinetic and potential energy, leading to changes in mechanical energy, unlike conservative forces which conserve mechanical energy. The distinction between conservative and non-conservative forces is highlighted, with examples illustrating their effects on an object's energy states.

20:12

💡 Power: The Rate of Doing Work

This section introduces the concept of power as the rate at which work is done or energy is transferred over time, explaining how it is measured and calculated. By comparing two individuals lifting weights over different durations, it illustrates how power relates to the speed of performing work, emphasizing that higher power results in faster energy transfer. The narrative further discusses units of power measurement and provides an alternative equation for calculating power based on force and velocity.

25:13

📊 Practice Problems on Work, Energy, and Power

The final parts of the script present a series of practice problems designed to apply and reinforce the concepts of work, energy, power, and their interrelations. These problems cover a range of topics including calculating kinetic energy, understanding the effects of changing mass and speed on kinetic energy, and determining the gravitational potential energy of objects. The practice problems also explore the work-energy theorem, kinetic and potential energy calculations, and the application of conservative forces, providing comprehensive exercises to solidify the viewer's understanding of these physical principles.

Mindmap

Keywords

💡Work

Work is defined as the product of the force applied to an object and the displacement of the object in the direction of the force. It's a measure of energy transfer when a force moves an object. In the video, work is introduced as a foundational concept in understanding how forces lead to energy transfer. For instance, when a force moves a block across a surface, work is done on the block, calculated as the force times displacement times the cosine of the angle between the force and displacement vectors, illustrating the relationship between force, movement, and energy transfer.

💡Energy

Energy is described as the capacity to do work. The video emphasizes that objects with energy can exert forces that perform work on other objects, transferring energy in the process. Energy exists in various forms, such as kinetic energy (energy of motion) and potential energy (stored energy). The video uses examples like a moving ball (kinetic energy) and a block elevated above ground level (potential energy) to illustrate these concepts, showing how energy enables objects to perform work.

💡Kinetic Energy

Kinetic energy is the energy an object possesses due to its motion. It's calculated as one-half the mass of the object times the square of its velocity. The video uses the example of a ball in motion to illustrate kinetic energy, explaining how moving objects can perform work on others due to their energy. The equation KE = 1/2 mv^2 provides a quantitative measure of this energy, showing how both mass and velocity contribute to an object's kinetic energy.

💡Potential Energy

Potential energy is the energy stored within an object due to its position, condition, or composition. The video focuses on gravitational potential energy, which is the energy stored in an object due to its height above ground. Calculated as the product of mass, gravitational acceleration, and height (mgh), this energy represents the potential to do work as the object falls. Examples include a block raised above ground level, illustrating how stored energy can be converted into kinetic energy.

💡Power

Power is defined as the rate at which work is done or energy is transferred over time. It is measured in watts (joules per second). The video illustrates this concept by comparing two individuals, John and Jared, lifting identical weights but at different speeds. John, who lifts the weight faster, demonstrates greater power because he transfers energy (does work) over a shorter period. This example highlights power's role in quantifying the efficiency and speed of energy transfer.

💡Newton's Third Law

Newton's Third Law states that for every action, there is an equal and opposite reaction. The video uses this law to explain interactions like a ball colliding with a block, where the ball exerts a force on the block (action force), and the block exerts an equal but opposite force on the ball (reaction force). This interaction illustrates the transfer of energy between objects and how forces lead to changes in kinetic energy, embodying the concept of action and reaction in physical systems.

💡Work-Energy Theorem

The Work-Energy Theorem states that the net work done on an object is equal to the change in its kinetic energy. This principle is used in the video to explain how forces acting on objects, like during a collision, result in changes in kinetic energy, illustrating the direct relationship between the work done by forces and the energy dynamics of the objects involved. The theorem is foundational in understanding how energy is transferred and conserved within systems.

💡Conservative Forces

Conservative forces, such as gravity, are forces where the work done does not depend on the path taken but only on the initial and final positions. The video mentions gravity as a conservative force, emphasizing how it can convert potential energy into kinetic energy without loss, maintaining the total mechanical energy of a system. This concept is crucial for understanding energy conservation in physics, especially in systems influenced by forces like gravity.

💡Non-Conservative Forces

Non-conservative forces, like friction or air resistance, lead to energy dissipation, meaning they do not conserve the total mechanical energy of a system. The video discusses how these forces can change an object's kinetic and potential energy, usually reducing the system's total energy. By contrast to conservative forces, non-conservative forces highlight real-world scenarios where energy is lost to surroundings, affecting the motion and energy of objects in a system.

💡Mechanical Energy

Mechanical energy is the sum of kinetic and potential energy in a system. The video illustrates mechanical energy conservation in the absence of non-conservative forces, using examples like a ball falling under gravity. It explains how the total mechanical energy (kinetic plus potential) remains constant in conservative systems, emphasizing the interconversion between kinetic and potential energy while highlighting the fundamental principle of energy conservation in mechanics.

Highlights

Work is accomplished by the action of a force.

Work is the product of the magnitude of the force and its displacement.

The work done by a force is affected by the angle between the force and displacement vectors.

An object with energy has the ability to do work.

Kinetic energy is present whenever an object is in motion.

Potential energy is stored energy, such as gravitational potential energy due to an object's height.

The work-energy theorem states that the work done by a force is equal to the change in an object's kinetic energy.

The direction of force and displacement vectors determines whether work is positive or negative.

When force and displacement vectors are perpendicular, the force does no work.

Mechanical energy is the sum of an object's kinetic and potential energy.

Conservative forces like gravity do not change the mechanical energy of a system.

Non-conservative forces, such as friction, can decrease the mechanical energy of a system.

Power is the rate at which work is done or energy is transferred.

Power can be calculated as work divided by time or as force times velocity.

The work done by a force can be found by calculating the area under the force-displacement curve.

The concept of work, energy, and power is fundamental in understanding the dynamics of physical systems.

Transcripts

Browse More Related Video

Mechanical Energy - Basic Overview

AP Physics C: Work, Energy, and Power Review (Mechanics)

Work and Energy

AP Physics 1 review of Energy and Work | Physics | Khan Academy

Energy intro (kinetic & potential) | Work & Energy | Physics | Khan Academy

AP Physics 1: Work, Energy and Power Review

Related Tags

Physics Concepts Work Calculation Energy Forms Mechanical Energy Kinetic and Potential Conservation Laws Force and Displacement Power and Velocity Newton's Laws Friction and Air Resistance