Ch. 1.10 Lines
TLDRThis educational video script delves into the concepts of linear equations and graphing. It explains the slope as the rate of change, using the rise over run method. The script covers how to graph lines using slope-intercept form and standard form, identifying key points like the y-intercept. It also discusses how to find equations for lines given various points and slopes, and introduces the concepts of parallel and perpendicular lines, providing examples to illustrate these relationships.
Takeaways
- 📚 The lesson focuses on understanding and graphing lines, including the concepts of slope and y-intercept.
- 📈 The slope of a line is defined as the rate of change, representing the ratio of vertical to horizontal change.
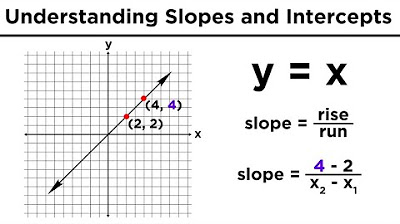
- 📍 The slope is calculated using the formula \( m = \frac{\Delta y}{\Delta x} \) or \( m = \frac{y_1 - y_0}{x_1 - x_0} \).
- 🔍 A line with a negative slope decreases as it moves from left to right, while a line with a positive slope increases.
- 🔺 A line with a zero slope is horizontal, and a line with an undefined slope is vertical, as it cannot be divided by zero.
- 👉 The slope-intercept form of a line is \( y = mx + b \), where \( m \) is the slope and \( b \) is the y-intercept.
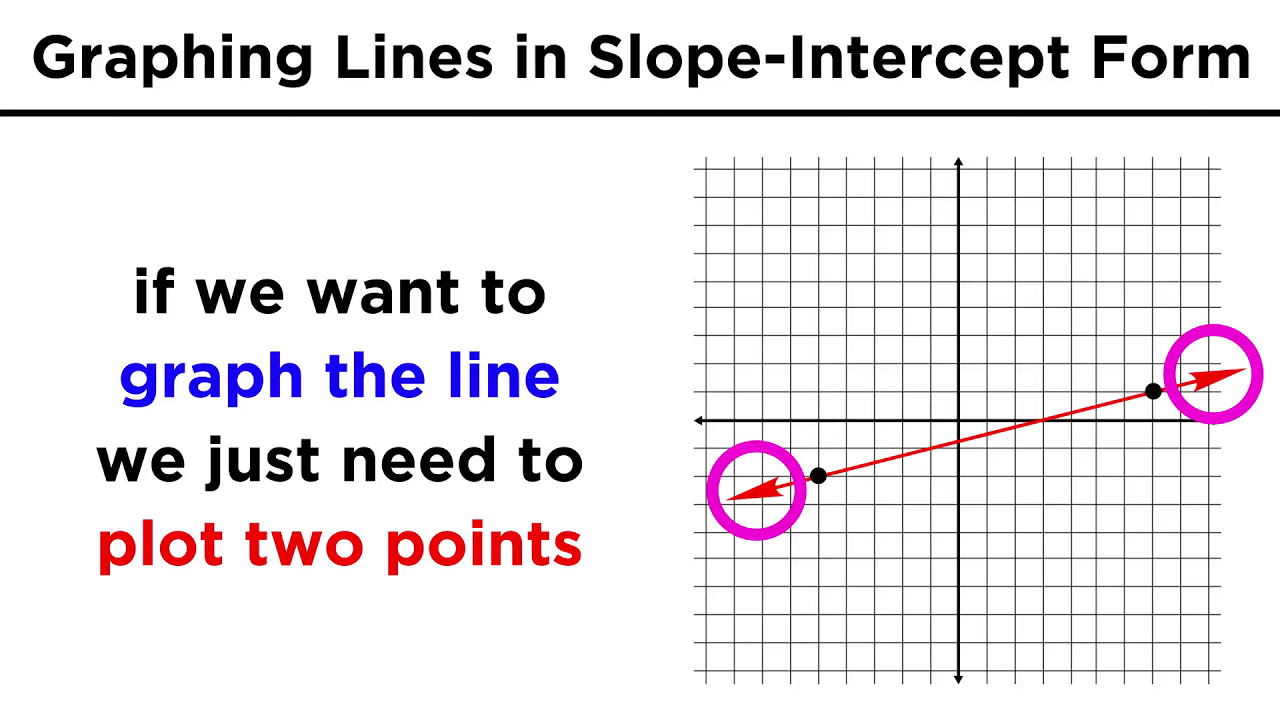
- 📝 Graphing a line involves starting at the y-intercept and applying the slope to find additional points on the line.
- 🔍 Standard form of a line is \( Ax + By = C \), which can be used to find the x and y-intercepts for graphing.
- 🔄 Parallel lines have the same slope and do not intersect, while perpendicular lines have slopes that are negative reciprocals of each other.
- 📐 The point-slope form of a line, \( y - y_0 = m(x - x_0) \), is useful when given a point and a slope to find the equation of a line.
- 📉 The process of finding the equation of a line from given information involves using the slope and specific points or intercepts to solve for the unknowns.
Q & A
What is the slope of a line and how is it calculated?
-The slope of a line is the rate at which the line increases or decreases. It is calculated as the ratio of the change in the vertical movement (change in y, denoted as Δy or y1 - y0) to the change in the horizontal movement (change in x, denoted as Δx or x1 - x0), often referred to as 'rise over run'.
How do you determine if a line has a positive, negative, zero, or undefined slope?
-A line has a positive slope if it moves upward as it moves from left to right. A negative slope indicates the line moves downward in the same direction. A zero slope means the line is horizontal and does not rise or fall. An undefined slope occurs when the line is vertical, as it represents an infinite rate of change and cannot be expressed as a finite ratio.
What is the y-intercept of a line and how does it relate to the graph of the line?
-The y-intercept is the point where the line intersects the y-axis. It is represented by the term 'b' in the slope-intercept form of a line, which is y = mx + b. The y-intercept is the y-coordinate of this point (0, b), and it represents the starting point of the line on the y-axis.
What is the slope-intercept form of a line and why is it preferred for graphing?
-The slope-intercept form of a line is y = mx + b, where 'm' is the slope and 'b' is the y-intercept. This form is preferred for graphing because it allows you to easily identify the initial point on the y-axis (y-intercept) and the rate of change (slope), which can be used to plot additional points and draw the line on a graph.
How do you graph a line given its standard form, such as 2x + 4y = 8?
-To graph a line given in standard form, first find the y-intercept by setting x to 0 and solving for y. Then find the x-intercept by setting y to 0 and solving for x. Plot these intercepts as points on the graph, and then draw a line through these points to represent the graph of the line.
What is the point-slope form of a line and how is it used for graphing?
-The point-slope form of a line is y - y0 = m(x - x0), where (x0, y0) is a given point on the line and 'm' is the slope. This form is used for graphing by first plotting the given point, then using the slope to determine the direction and distance to move up and down (rise) and left and right (run) to plot additional points and draw the line.
How can you find the equation of a line if you are given two points?
-To find the equation of a line given two points, first calculate the slope using the formula m = (y2 - y1) / (x2 - x1). Then use one of the points and the slope in the point-slope form y - y1 = m(x - x1), and solve for 'b' to get the slope-intercept form y = mx + b.
What is the relationship between parallel lines in terms of their slopes?
-Parallel lines have the same slope. This means that they increase or decrease at the same rate and never intersect, regardless of how far they are extended in the positive or negative direction.
How do you determine if two lines are perpendicular, and what is the relationship between their slopes?
-Two lines are perpendicular if they intersect at a 90-degree angle. The slopes of perpendicular lines are negative reciprocals of each other. If the slope of one line is 'm', the slope of the perpendicular line would be -1/m.
Can you provide an example of finding a line perpendicular to a given line and passing through a specific point?
-To find a line perpendicular to a given line and passing through a specific point, first determine the slope of the given line. The slope of the perpendicular line will be the negative reciprocal of this slope. Then use the point and the new slope in the point-slope form to find the equation of the perpendicular line.
Outlines
📚 Introduction to Lines and Slope
The instructor begins by welcoming the class and introducing the topic of lines, following the previous lesson on the rectangular coordinate system. The focus is on understanding the slope of a line, defined as the rate of increase or decrease, represented as the ratio of the vertical change to the horizontal change. The concept of slope is illustrated with a grid, using points and the change in x and y coordinates to calculate it. The explanation includes the definition of slope as 'rise over run' or 'change in y over change in x', and the implications of positive, negative, zero, and undefined slopes are discussed with examples. The instructor also introduces the y-intercept and the slope-intercept form of a line, y = mx + b, as the preferred form for equations.
📈 Graphing Lines and Intercepts
This section delves into the process of graphing lines, starting with the slope-intercept form and moving to the standard form. The instructor explains how to graph a line by using the initial value (y-intercept) and applying the slope in both forward and backward directions. The concept of x and y-intercepts is introduced for standard form equations, and the method to find these intercepts is explained. The instructor provides an example of graphing the equation y = 2x + 3 by using the initial value and slope, and then graphs the equation 2x + 4y = 8 by finding the intercepts. The process of transforming standard form into slope-intercept form for easier graphing is also discussed.
📝 Equations and Forms of a Line
The instructor discusses different forms of equations for lines and their applications in graphing. The point-slope form is introduced as the easiest method when a point and a slope are given. The slope-intercept form is reiterated as the preferred form for equations, especially when given the y-intercept and slope. The instructor also explains how to derive the equation of a line when given two points, emphasizing the use of the slope-intercept form over the point-slope form. The relationship between graphing and modeling is highlighted, stating that if one has enough information to graph a line, they can also create the equation for that line.
🔍 Deriving Line Equations from Given Information
Building on the previous discussion, the instructor explains how to derive the equation of a line when given various pieces of information, such as a y-intercept and slope, any point and a slope, or two points. The method involves plugging the given values into the slope-intercept form and solving for the unknown constant, b. The point-slope form is used as a tool to find the y-intercept when only a point and slope are given, and the slope is calculated from two given points to find the equation of a line. The process is demonstrated with algebraic manipulation to arrive at the desired form, y = mx + b.
🔄 Parallel and Perpendicular Lines
The instructor introduces the concepts of parallel and perpendicular lines, explaining that parallel lines have the same slope and never intersect, while perpendicular lines intersect at a 90-degree angle and have slopes that are negative reciprocals of each other. The symbols for parallel and perpendicular lines are given, and the mathematical relationship between the slopes of perpendicular lines is detailed. An example is provided to illustrate how to find a line perpendicular to a given line that passes through a specific point, emphasizing the importance of correctly identifying the slope of the original line before proceeding.
📐 Constructing Specific Lines: Perpendicular and Parallel
In this final paragraph, the instructor presents a problem involving the construction of specific lines that are either parallel or perpendicular to a given line and pass through a given point. The process begins with finding the slope and equation of the original line, l1, using two given points. Once l1 is established, the instructor demonstrates how to find the equation for a parallel line, l2, that passes through another given point, ensuring it has the same slope as l1. The instructor then explains how to find the equation for a perpendicular line, l3, which also passes through the same point, emphasizing the need to use the negative reciprocal of the slope of l1. The solution includes algebraic steps to solve for the y-intercept of l2 and l3, and the final equations for these lines are provided.
Mindmap
Keywords
💡Slope
💡Line
💡Y-intercept
💡Graphing
💡Slope-Intercept Form
💡Standard Form
💡Point-Slope Form
💡Parallel Lines
💡Perpendicular Lines
💡Undefined Slope
Highlights
Introduction to the concept of lines and their graphs in the context of the rectangular coordinate system.
Explanation of the slope as the rate of increase or decrease of a line, defined as the ratio of vertical to horizontal change.
Graphical representation of slope using a grid, illustrating how it is calculated between two points.
Differentiation between positive and negative slopes, and the concept of zero slope indicating a flat line.
Introduction of undefined slope in the context of vertical lines where the ratio of change is indeterminate.
Discussion of the y-intercept as the point where a line crosses the y-axis.
Introduction of the slope-intercept form of a line (y = mx + b) as the preferred equation form for lines.
Demonstration of graphing a line using the slope-intercept form, starting from the y-intercept and applying the slope.
Explanation of graphing a line when the slope is large and the application of the slope in both forward and backward directions.
Conversion of standard form equations (Ax + By = C) to slope-intercept form for easier graphing.
Illustration of graphing a line given the equation y = 2x + 3 using the slope-intercept form.
Example of graphing a line given in standard form, 2x + 4y = 8, by finding the x and y-intercepts.
Introduction of the point-slope form (y - y₀ = m(x - x₀)) for graphing a line with a given point and slope.
Discussion on the relationship between graphing lines and modeling, emphasizing that sufficient information for graphing also provides enough information to create an equation.
Explanation of how to find the equation of a line given a y-intercept and a slope by plugging values into the slope-intercept form.
Process of finding the equation of a line given any point and a slope using the point-slope form and solving for the y-intercept.
Clarification on the use of two points to determine a line's equation by finding the slope and applying it in the slope-intercept form.
Introduction to the concepts of parallel and perpendicular lines, defining their slopes as equal and negative reciprocals respectively.
Example problem involving finding equations of lines that are perpendicular to a given line and pass through a specified point.
Emphasis on the importance of correctly finding the equation of the first line (l1) as it affects the accuracy of subsequent lines (l2 and l3).
Final summary and reminder of the significance of the concepts covered, their potential appearance in exams, and the importance of checking work in mathematics.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: