Probability Part 2: Updating Your Beliefs with Bayes: Crash Course Statistics #14
TLDRThis video explains conditional probability and Bayes' theorem. It uses examples like spam filters to show how new information can update beliefs about probabilities. The video discusses Thomas Bayes' work on updating probabilities with new evidence. It also covers techniques like simulations to build intuition about concepts including the Law of Large Numbers. Overall, the video explores how probability and statistics can evolve with additional data rather than occur in a vacuum.
Takeaways
- 😀 Conditional probability allows us to calculate the probability of one event happening, given that another event has already occurred
- 📊 Bayes' Theorem builds on conditional probability to update beliefs based on new evidence
- 📈 Naive Bayes filters use Bayes' Theorem to identify spam emails
- 🌟 Reverend Thomas Bayes contributed the idea of 'updating beliefs' in statistics
- 🎴 Simulations can demonstrate probability rules by generating data based on those rules
- 🔢 The Law of Large Numbers says that as sample sizes grow, the sample mean gets closer to the true population mean
- 🎰 Casinos make money in the long run based on the Law of Large Numbers, despite individual wins and losses
- 🤔 Bayesian statistics involves continuously updating beliefs based on accumulating evidence
- 🌎 Bayes' Theorem is used in many fields like medicine, robotics and physics
- 📊 Frequentist statistics relies less on prior knowledge than Bayesian methods
Q & A
What is conditional probability and how does it relate to Bayes' Theorem?
-Conditional probability is the probability of one event occurring given that another event has already occurred. Bayes' Theorem expands on conditional probability to allow us to update our beliefs about probabilities based on new evidence. It relates the probability of B given A to the probabilities of A and B on their own.
How do naive Bayes filters work to detect spam emails?
-Naive Bayes filters use a version of Bayes' Theorem to classify emails as spam or not spam. They look at the probability an email is spam given that it contains certain words like "Nigerian Prince." By comparing this conditional probability to the base rate of spam, they can effectively filter spam emails.
Who was Reverend Thomas Bayes and what was his contribution?
-Reverend Thomas Bayes was an 18th century Presbyterian minister who also worked in mathematics. His biggest contribution was formulating Bayes' Theorem, which allows probabilities to be updated based on new evidence. This laid the foundation for Bayesian statistics.
How do we use simulations to understand probability concepts?
-We can create simulations by programming rules that generate random data matching certain probabilities. These simulations essentially create pretend universes where we can watch probability at work. They provide intuition and demonstration without needing the math.
What is the law of large numbers?
-The law of large numbers says that as sample sizes get bigger, the sample mean gets closer and closer to the true population mean. So by taking a large enough sample, we can make good inferences about the overall population.
How did Reverend Bayes explain updating beliefs?
-In a thought experiment, Reverend Bayes imagined guessing where a ball landed on a pool table without being able to see it. As more balls are dropped, whether they land left or right of the original ball provides evidence to update your guess of where the original ball is.
What are some applications of Bayesian statistics?
-Bayesian statistics is used in many fields including medicine, ecology, physics, and more. It can be used to compare treatments, help robots learn language, analyze cancer data, study populations, and make inferences from incomplete information.
How does the law of large numbers allow casinos to be profitable?
-Although individual players may win or lose money, over hundreds of thousands of bets the actual probability emerges. The casino looks at a huge sample size of bets so they earn a predictable profit, while each player only sees their own small sample.
What is the difference between frequentist and Bayesian statistics?
-Frequentist statistics involves probability in a vacuum, like figuring out the frequency of heads from a large number of coin flips. Bayesian statistics incorporates prior knowledge and continuously updates probabilities as new data comes in.
What are some ways we update our beliefs every day?
-We update our beliefs daily in small ways by integrating new events and information into our worldview. For example, getting another spam email with "Nigerian Prince" makes us believe the next similar email is more likely to be spam as well.
Outlines
😊 Introducing Conditional Probability
The paragraph introduces the concept of conditional probability, which calculates the probability of one event happening given that another event has already occurred. It provides the general formula for conditional probability and a specific example of calculating the probability that an email is spam given that it contains the words "Nigerian Prince".
😲 Explaining Bayes' Theorem
The paragraph explains Bayes' Theorem, which expands on the conditional probability formula. It allows calculating the probability of one event happening given another event, while also considering the base probabilities of those events. The theorem has enabled new ways of analyzing data and updating beliefs based on evidence.
📈 Demonstrating Law of Large Numbers
The paragraph demonstrates the Law of Large Numbers using simulations. As sample sizes increase, the sample mean gets closer to the true population mean. This allows making inferences about populations from samples and explains why casinos make money over many bets.
Mindmap
Keywords
💡Conditional Probability
💡Bayes' Theorem
💡Bayesian Statistics
💡Naive Bayes Filter
💡Updating Beliefs
💡Law of Large Numbers
💡Simulation
💡Sample Mean
💡Sensitivity
💡Specificity
Highlights
Conditional Probability tells us the probability of one event, given that a second event has already happened
Bayes Theorem allows us to figure out the probability that an email is spam using information we already have, like the presence of certain words
Bayesian statistics is about updating your beliefs based on new information
Each new piece of information allows us to change our beliefs about a hypothesis
Bayesian Statistics is being used in many fields like medicine, ecology, and physics
Simulations demonstrate probability by creating a pretend universe that follows set rules
The Law of Large Numbers says sample means get closer to the true population mean as sample size increases
The Law of Large Numbers allows us to make guesses about populations based on samples
Casinos make money in the long run because they look at a huge sample of bets and payouts
The Bayesian framework shows that every data point can update your beliefs, not completely change them
Simulations allow us to understand concepts when the underlying mechanics aren't clear
We are continuously accumulating evidence and modifying our beliefs
Maybe one day we’ll all start sincerely emailing each other about Nigerian Princes
Then we’re gonna have to do some belief-updating
Thanks for watching. I’ll see you next time
Transcripts
Browse More Related Video
You Know I'm All About that Bayes: Crash Course Statistics #24

Bayes in Science and Everyday Life: Crash Course Statistics #25

Probability Formulas, Symbols & Notations - Marginal, Joint, & Conditional Probabilities
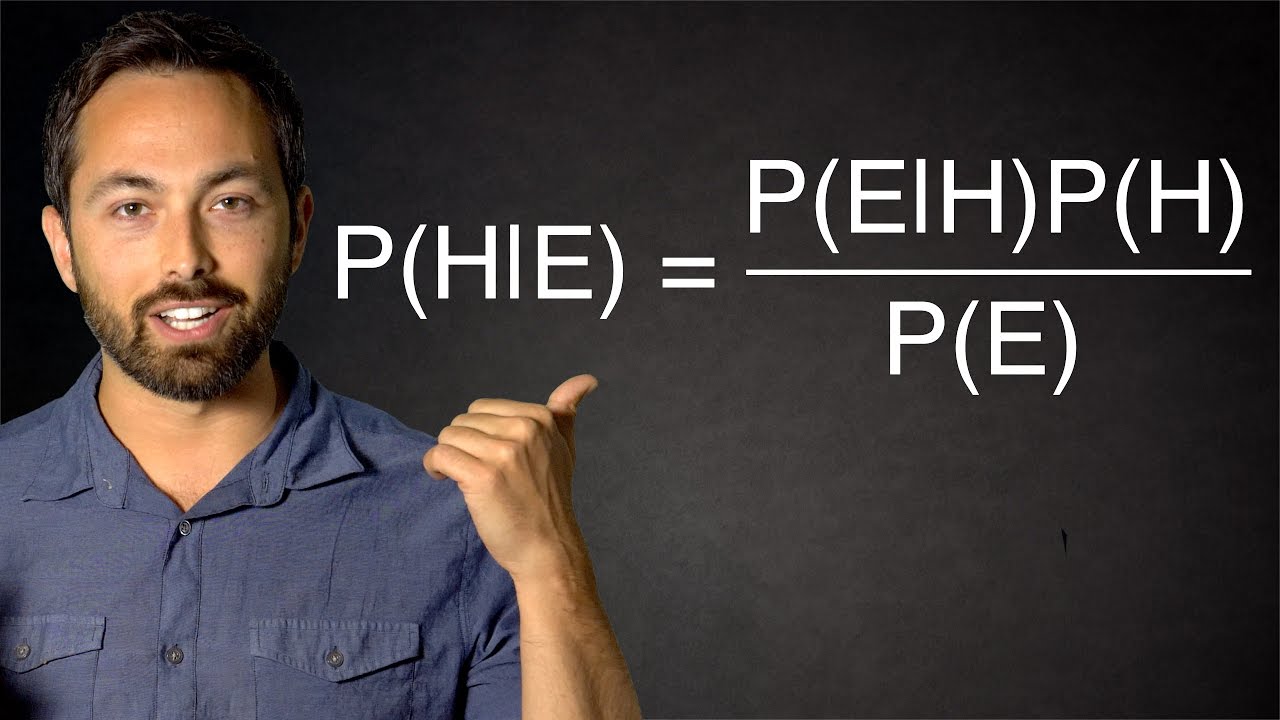
The Bayesian Trap
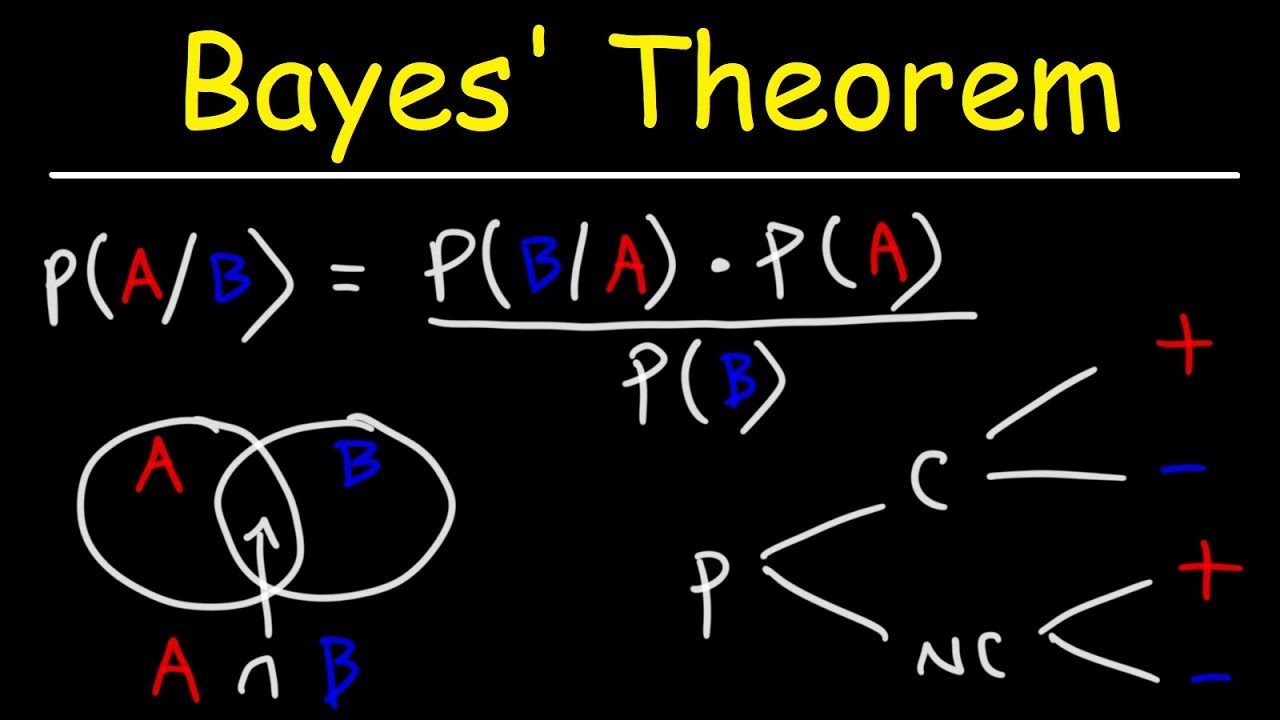
Bayes' Theorem of Probability With Tree Diagrams & Venn Diagrams

Probability: Bayes' Theorem
5.0 / 5 (0 votes)
Thanks for rating: