Linear Functions
TLDRThis video tutorial comprehensively covers the fundamentals of linear functions, walking through the calculation of slopes, the identification of y-intercepts, and the graphing of linear equations in various forms. It explains how to find the slope between two points, derive the equation of a line from a point and a slope, and convert between slope-intercept form, standard form, and point-slope form. The video also demonstrates how to graph vertical and horizontal lines, calculate x and y intercepts, and how to handle special cases like perpendicular and parallel lines. The step-by-step approach ensures clarity and ease of understanding, making it an excellent resource for anyone looking to strengthen their grasp of linear functions.
Takeaways
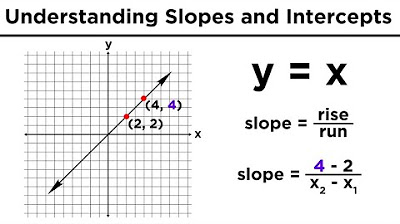
- 📈 The slope of a line is calculated using the formula (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are the coordinates of two points on the line.
- 📑 A linear equation in slope-intercept form is written as y = mx + b, where m is the slope and b is the y-intercept.
- 🔍 To graph the equation x = c, the graph is a vertical line at x = c, and for y = d, it's a horizontal line at y = d.
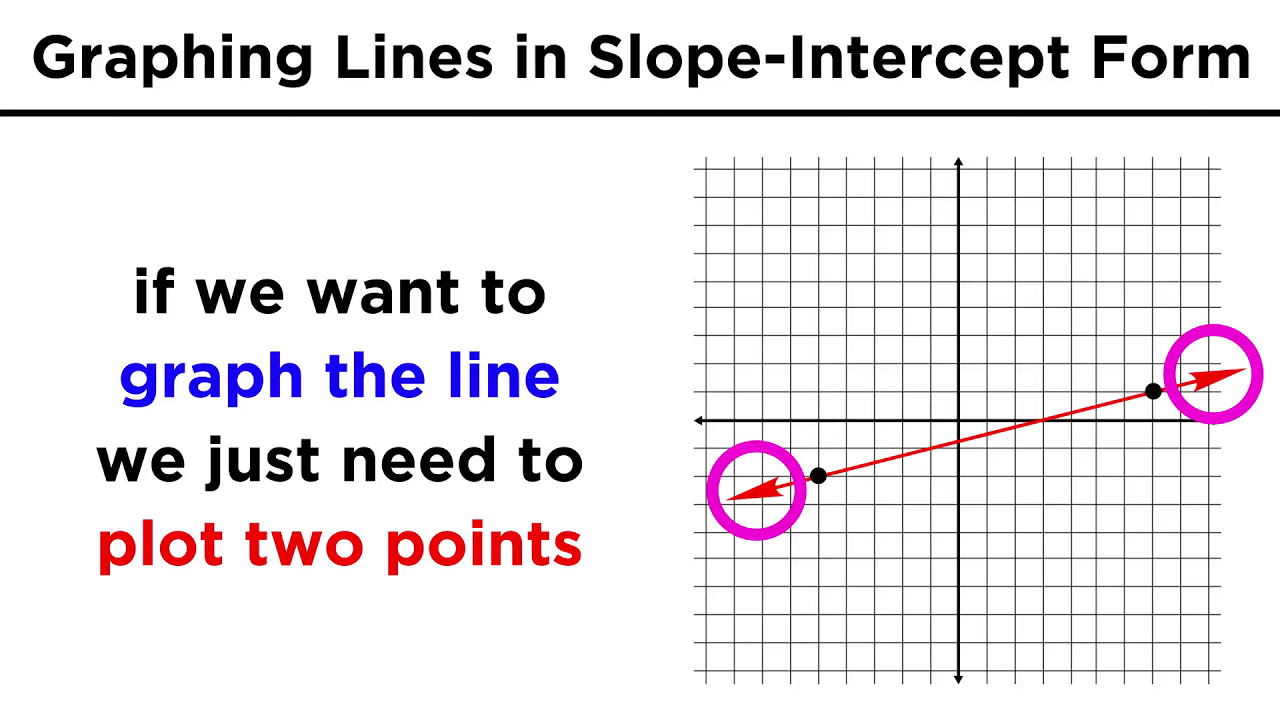
- 📈 The slope-intercept method involves plotting the y-intercept and using the slope to find additional points to draw the line.
- 🔗 To find x and y-intercepts, set y to 0 for x-intercepts and x to 0 for y-intercepts in the given equation.
- 📝 The standard form of a linear equation is Ax + By = C, and it can be graphed by finding intercepts and plotting the line.
- 🔑 The point-slope form of a line is given by y - y1 = m(x - x1), where m is the slope and (x1, y1) is a point on the line.
- 🔄 Parallel lines have the same slope, which can be used to find the equation of a line parallel to a given line passing through a point.
- ⊥ Perpendicular lines have slopes that are negative reciprocals of each other, which can be used to find the equation of a line perpendicular to a given line passing through a point.
- 🔄 Converting between point-slope form and slope-intercept form involves algebraic manipulation, such as distributing and simplifying the equation.
Q & A
What is the formula used to calculate the slope of a line passing through two points?
-The formula to calculate the slope (m) of a line passing through two points (x1, y1) and (x2, y2) is (y2 - y1) / (x2 - x1).
How do you find the slope and y-intercept of the line represented by the equation y = 2x - 3?
-The equation y = 2x - 3 is in slope-intercept form (y = mx + b), where m is the slope and b is the y-intercept. Thus, the slope (m) is 2, and the y-intercept (b) is -3.
What are the two types of lines represented by the equations x = 2 and y = 3?
-The equation x = 2 represents a vertical line, while the equation y = 3 represents a horizontal line.
How do you graph the equation y = 3x - 2 using the slope-intercept method?
-To graph y = 3x - 2, start with the y-intercept at (0, -2). Then, move one unit to the right and rise three units to get the next point (1, 1). Continue this pattern to form the line.
What are the x and y-intercepts of the equation 2x - 3y = 6?
-For the x-intercept, set y to 0: 2x = 6, so x = 3. For the y-intercept, set x to 0: -3y = 6, so y = -2. The intercepts are (3, 0) and (0, -2).
What is the equation of the line passing through the point (2, 5) with a slope of 3?
-Using the point-slope form, the equation is y - 5 = 3(x - 2). Converting to slope-intercept form gives y = 3x - 1.
How do you find the equation of the line passing through the points (-3, 1) and (2, -4)?
-Calculate the slope: (-4 - 1) / (2 - (-3)) = -5 / 5 = -1. Use the point-slope form with one of the points, say (-3, 1): y - 1 = -1(x - (-3)). Simplify to get y = -x + 2.
What is the equation of the line parallel to the line 2x + 5y - 3 and passing through the point (-3, -2)?
-The slope of the given line is -2/5. The parallel line will have the same slope. Using the point-slope form with the point (-3, -2) gives y + 2 = (-2/5)(x - (-3)). Simplifying yields y = (-2/5)x + 4/5.
What is the equation of the line perpendicular to the line 3x - 4y + 5 and passing through the point (-4, -3)?
-The slope of the given line is 3/4. The perpendicular line's slope will be the negative reciprocal, which is -4/3. Using the point-slope form with the point (-4, -3) gives y + 3 = (-4/3)(x - (-4)). Simplify to get y = (-4/3)x - 20/3.
How do you convert a linear equation from point-slope form to slope-intercept form?
-To convert from point-slope form (y - y1 = m(x - x1)) to slope-intercept form (y = mx + b), distribute the slope (m) to the terms inside the parentheses and then add y1 to both sides of the equation to solve for y.
What is the significance of the slope-intercept form of a linear equation?
-The slope-intercept form (y = mx + b) is significant because it directly shows the slope (m) of the line and the y-intercept (b), which is the point where the line crosses the y-axis.
What is the standard form of a linear equation and how does it differ from the slope-intercept form?
-The standard form of a linear equation is Ax + By = C, where A, B, and C are constants. It differs from the slope-intercept form in that it does not explicitly show the slope and y-intercept, requiring rearrangement for comparison.
Outlines
📚 Introduction to Linear Functions and Problem Solving
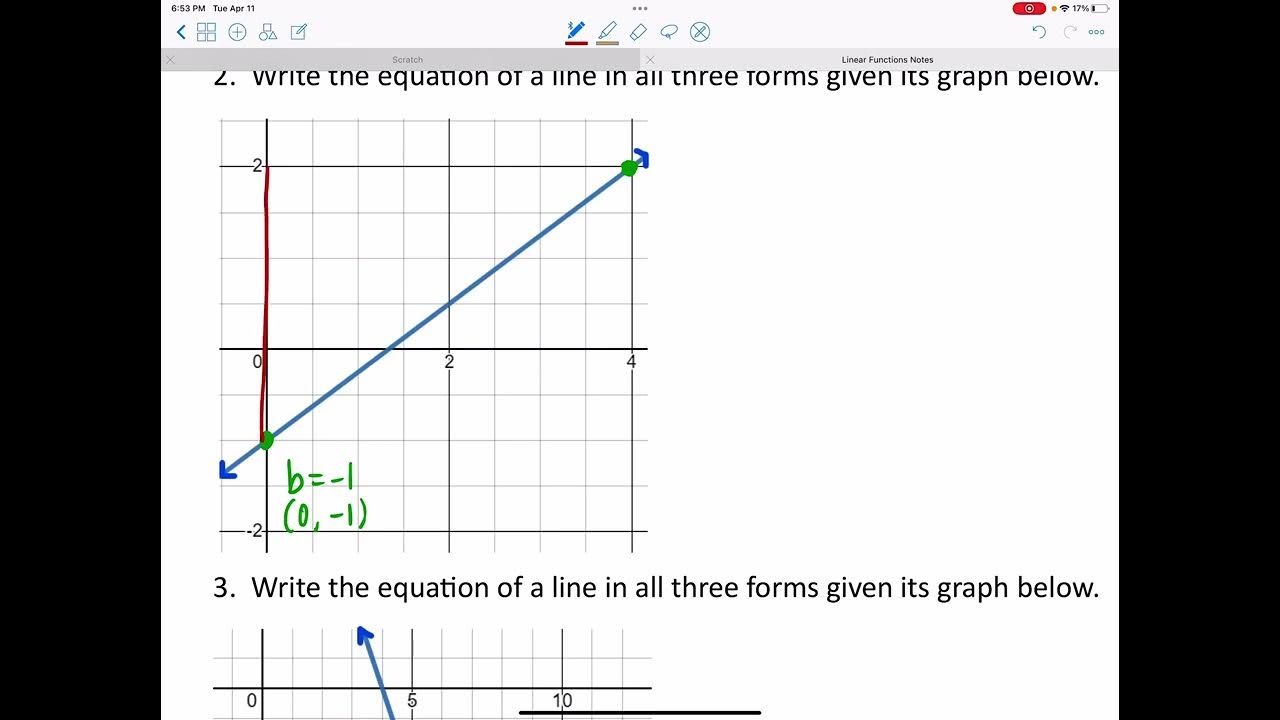
This paragraph introduces the topic of linear functions and begins with solving a problem to find the slope of a line passing through two given points. The formula for calculating the slope is explained, and the process is demonstrated using specific coordinates. Following this, the video explains how to determine the slope and y-intercept of a line given in slope-intercept form. The concept of graphing lines and equations, both vertical and horizontal, is also covered. The paragraph concludes with a problem-solving example using the slope-intercept method to graph an equation.
📐 Graphing Linear Equations in Standard Form
The second paragraph focuses on graphing linear equations in standard form. It explains the process of finding x and y-intercepts and graphing them to represent the equation visually. The paragraph also introduces the concept of slope-intercept form, standard form, and point-slope form, emphasizing the importance of familiarity with these forms for graphing and solving linear equations. The paragraph concludes with a detailed walkthrough of graphing a linear equation from standard form to finding the x and y-intercepts and connecting them to form the graph.
🔍 Writing Equations of Lines with Given Conditions
This paragraph delves into the methods of writing linear equations when provided with certain conditions such as a point and a slope, or two points for which the slope is unknown. The point-slope formula is introduced and used to derive the equation of a line. The process of converting the point-slope form to slope-intercept form is explained with a step-by-step example. The paragraph also covers how to find the slope of a given line and use it to write the equation of a parallel or perpendicular line. The summary includes detailed calculations and the final equations derived from the given conditions.
Mindmap
Keywords
💡slope
💡line
💡y-intercept
💡point-slope form
💡slope-intercept form
💡standard form
💡graphing
💡x-intercept
💡perpendicular lines
💡parallel lines
💡linear equation
Highlights
The video covers basic questions related to linear functions, starting with calculating the slope of a line passing through two given points.
The formula for calculating the slope between two points is y2 - y1 divided by x2 - x1.
An example is given where the slope of the line passing through the points (2, -3) and (4, 5) is calculated to be 4.
The video explains the slope-intercept form of a line, y = mx + b, where m is the slope and b is the y-intercept.
The equation y = 2x - 3 is analyzed to show a slope of 2 and a y-intercept of -3.
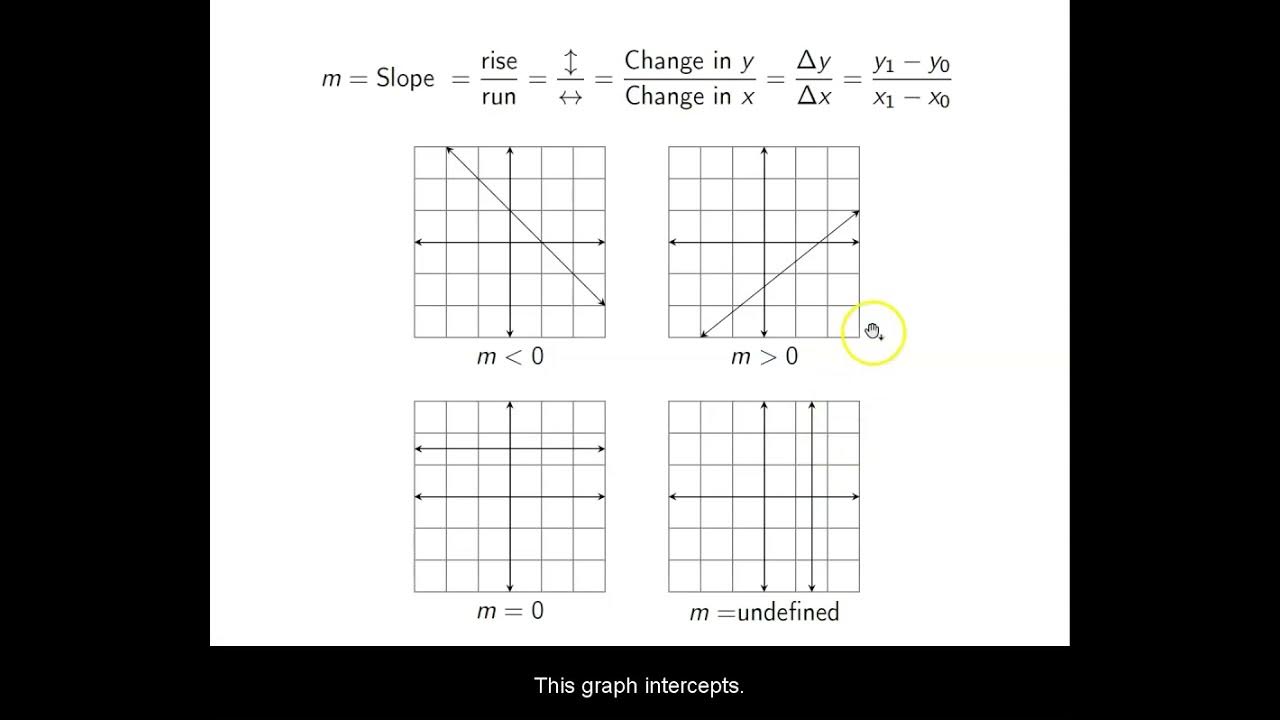
The method for graphing equations as vertical or horizontal lines is demonstrated with the equations x = 2 and y = 3.
The process of graphing a line using the slope-intercept method is detailed, with the equation y = 3x - 2 and the corresponding points (0, -2), (1, 1), and (2, 4).
The method for graphing a linear equation in standard form using x and y-intercepts is explained, with the example equation 2x - 3y = 6.
The three forms of linear equations are introduced: slope-intercept form, standard form, and point-slope form.
The point-slope formula is used to find the equation of a line passing through a given point with a specified slope, demonstrated with the point (2, 5) and slope 3.
The process of finding the equation of a line passing through two given points is outlined, with the example points (-3, 1) and (2, -4).
The concept of parallel lines having the same slope is discussed, with an example of finding a line parallel to y = 2x + 5/3.
The method for finding the equation of a line perpendicular to a given line and passing through a specific point is explained, with an example of a line perpendicular to 3x - 4y + 5.
The negative reciprocal relationship between the slopes of perpendicular lines is highlighted, with an example of finding the slope of a line perpendicular to one with a slope of 3/4.
The general approach to solving linear equations and graphing lines is summarized, showcasing the importance of understanding different forms of linear equations and their applications.
The video serves as a comprehensive guide for beginners learning about linear functions, their graphs, and the mathematical tools used to analyze them.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: