Graphing Lines in Standard Form (ax + by = c)
TLDRThe script discusses two common forms for expressing linear equations: slope-intercept form (y=mx+b) and standard form (Ax+By=C). It explains how to quickly graph lines using the standard form by finding x- and y-intercepts. It also shows how to convert between the two forms, noting that standard form requires integer coefficients in lowest ratio. The summary covers when each form is preferable: slope-intercept for finding slope, standard for rapidly graphing using intercepts. It aims to provide the key differences and interconversions between these fundamental forms for expressing linear equations.
Takeaways
- 😀 There are two main forms for linear equations: slope-intercept form (y = mx + b) and standard form (Ax + By = C)
- 😇 Standard form is useful for quickly finding the x and y intercepts of a line by plugging in 0 for x or y
- 🧐 To find the slope of a line from its standard form equation, you can use the intercepts or convert it to slope-intercept form
- 🤓 To convert from standard to slope-intercept form, solve the equation for y by subtracting Ax from both sides first
- 😎 To convert slope-intercept form to standard form, ensure A, B and C are integers with no common factors
- 🤔 When writing equations in standard form, use the lowest possible ratio of coefficients A, B and C
- 👍 Standard form is useful when graphing lines quickly using the intercepts
- 😊 Slope-intercept form directly gives you the slope and y-intercept for analysis
- 🙂 You can convert between standard and slope-intercept forms easily as needed
- 😃 But always try to use the simplest form of a linear equation when possible
Q & A
What are the two main forms that linear equations can take?
-The two main forms are the slope-intercept form (y = mx + b) and the standard form (Ax + By = C).
What is the advantage of using standard form to graph a line?
-Standard form makes it easy to quickly identify the x and y-intercepts of a line, which provides two points to plot the line.
How do you find the y-intercept from an equation in standard form?
-Plug in 0 for x. The x term will drop out, leaving you to solve for y.
How do you find the x-intercept from an equation in standard form?
-Plug in 0 for y. The y term will drop out, leaving you to solve for x.
What is the disadvantage of standard form compared to slope-intercept form?
-It is trickier to identify the slope of the line directly from standard form.
How can you calculate the slope if you only have the equation in standard form?
-Use the intercepts to calculate rise/run, or convert the equation to slope-intercept form to read off the slope.
What restrictions exist on the coefficients A, B, and C in standard form?
-They must be integers, and should be in the lowest possible ratio.
How do you convert from standard form to slope-intercept form?
-Solve the equation for y - first subtract the x term to isolate y, then divide both sides by the y coefficient.
How do you convert from slope-intercept form to standard form?
-Ensure all coefficients are integers by multiplying through if needed. Then isolate the constant on one side.
When converting to standard form, why is having the simplest ratio of coefficients important?
-You want the equation in lowest terms - the simplest ratio of integers. This allows the easiest identification of intercepts.
Outlines
📈 Graphing Lines in Standard Form
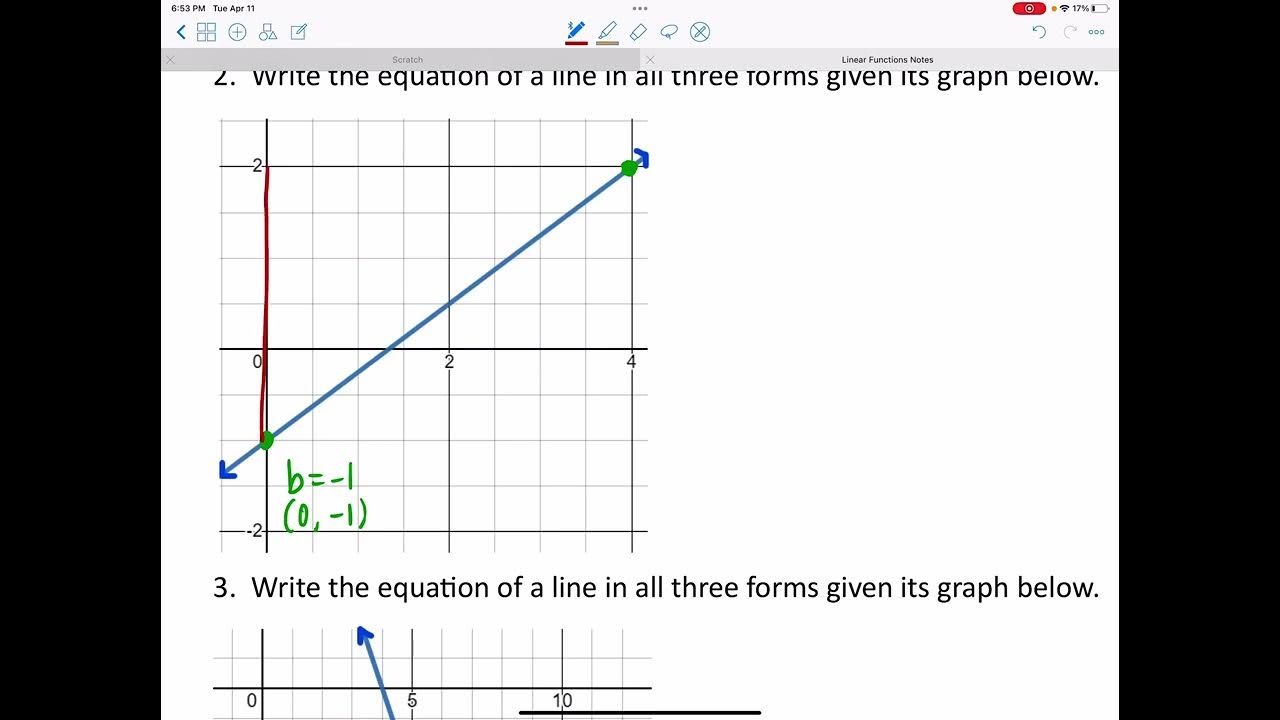
This paragraph explains the standard form for linear equations (AX + BY = C) and how it can be useful for quickly graphing lines by finding the x and y intercepts. It provides an example equation in standard form and shows how to find the intercepts and plot the line.
😎 Converting Between Standard and Slope-Intercept Forms
This paragraph explains how to convert between the standard and slope-intercept forms of a linear equation. It shows how to find the slope from a line in standard form and how to convert from slope-intercept to standard form, stressing that the A, B, and C terms must be integer values in simplest ratio.
Mindmap
Keywords
💡slope-intercept form
💡standard form
💡intercepts
💡graph
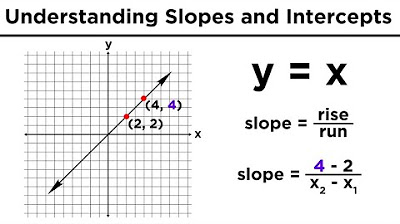
💡slope
💡ratio
💡convert
💡simplify
💡manipulate
💡coordinate plane
Highlights
We understand how to graph lines using the slope-intercept form, but there is another form called the standard form that can also represent linear relationships
The standard form is AX + BY = C. It can be useful for quickly graphing a line by finding the x and y intercepts
To find the y-intercept, plug in 0 for X. To find the x-intercept, plug in 0 for Y. Then plot those two points to graph the line
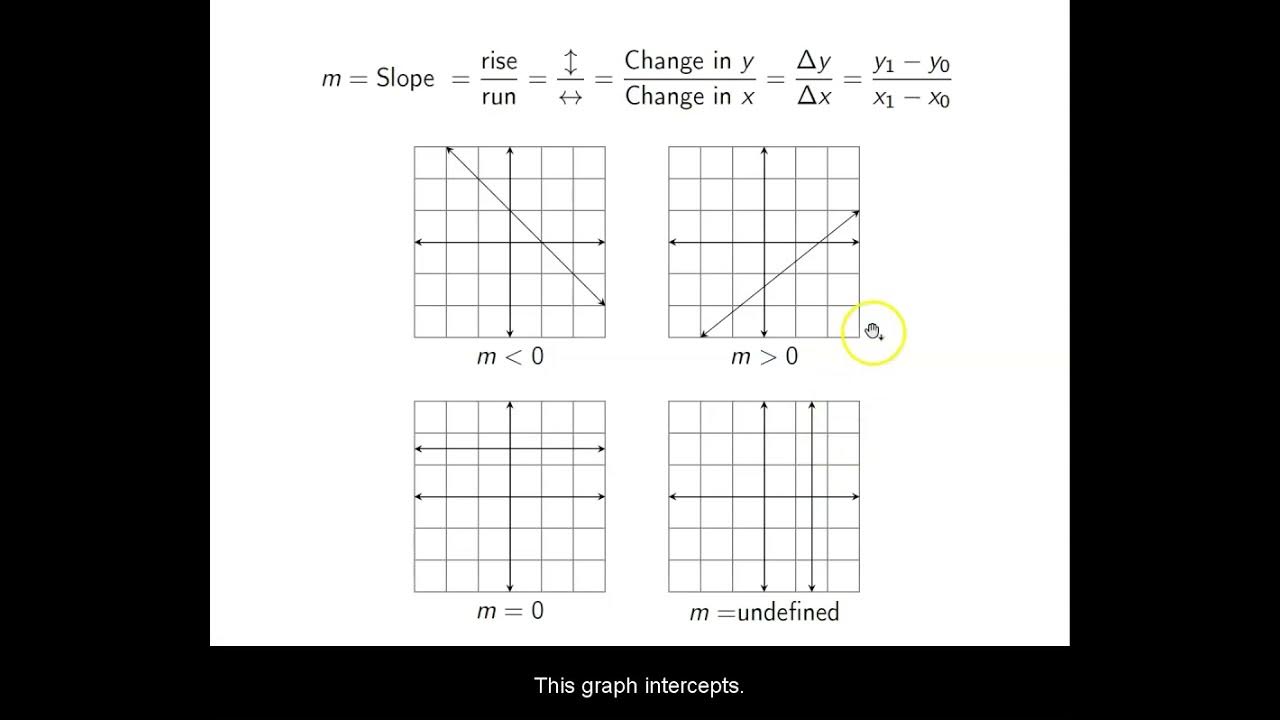
While standard form is good for finding intercepts and graphing quickly, slope-intercept form is better for determining the slope of a line
To find the slope from a line in standard form, calculate it using the coordinates of the two intercept points, or convert the equation to slope-intercept form
To convert from standard to slope-intercept form, solve the standard form equation for Y
To convert from slope-intercept to standard form, ensure A, B and C are integer values in the simplest ratio possible
Having both standard and slope-intercept forms for linear equations allows using the best form for the specific task like finding intercepts, slope or graphing
The standard form of a linear equation is AX + BY = C, where A, B and C are integers that are in the simplest ratio possible
The y-intercept can be found by plugging in 0 for X, and the x-intercept by plugging in 0 for Y
Standard form is useful for quickly graphing lines by finding the intercepts, while slope-intercept form is better for determining slope
To find slope from standard form, either use intercept coordinates or convert to slope-intercept form
To convert between forms, solve standard form for Y to get slope-intercept form, or ensure simplest integer ratio for slope-intercept to standard
Having both forms available allows choosing the best one for specific tasks like finding intercepts, slope or graphing lines
When writing linear equations, using the simplest integer ratio in standard form or explicitly showing slope in slope-intercept form makes analysis and graphing easier
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: