Linear Functions
TLDRThe video script provides an in-depth review of linear functions, focusing on their relevance to calculus. It emphasizes the importance of understanding derivatives, which are essentially the slopes of the tangent lines to a function's graph at a given point. The script covers various forms of linear functions, including slope-intercept form (y = mx + b), point-slope form (y - y1 = m(x - x1)), and standard form (ax + by = c). Through different scenarios, it demonstrates how to calculate the slope and write linear functions in these forms given different sets of information, such as the slope and y-intercept, a graph, or specific points. The lesson also touches on the concept of orientation in relation to the slope's positive or negative value, indicating whether a line increases or decreases. The ability to work with linear functions and their various forms is highlighted as crucial for success in calculus.
Takeaways
- 📚 The lesson is a review of linear functions with a focus on their application in pre-calculus and calculus.
- 🔍 Derivatives are a key concept in calculus, and they are related to the slope of the tangent line to a function at a given point.
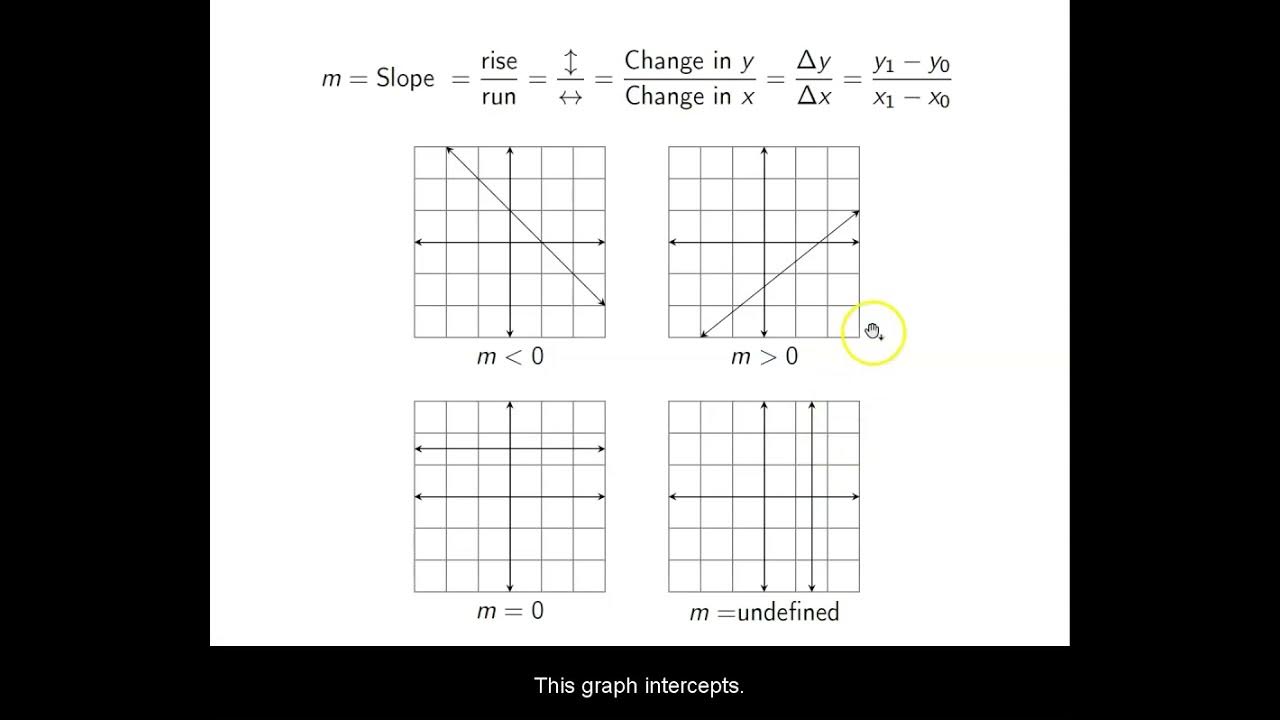
- 📈 Understanding slope is crucial as it measures the steepness and orientation of a line, which is essential for calculus.
- 📐 Slope is defined as the rise over run, which is the change in y-values over the change in x-values between two points on a line.
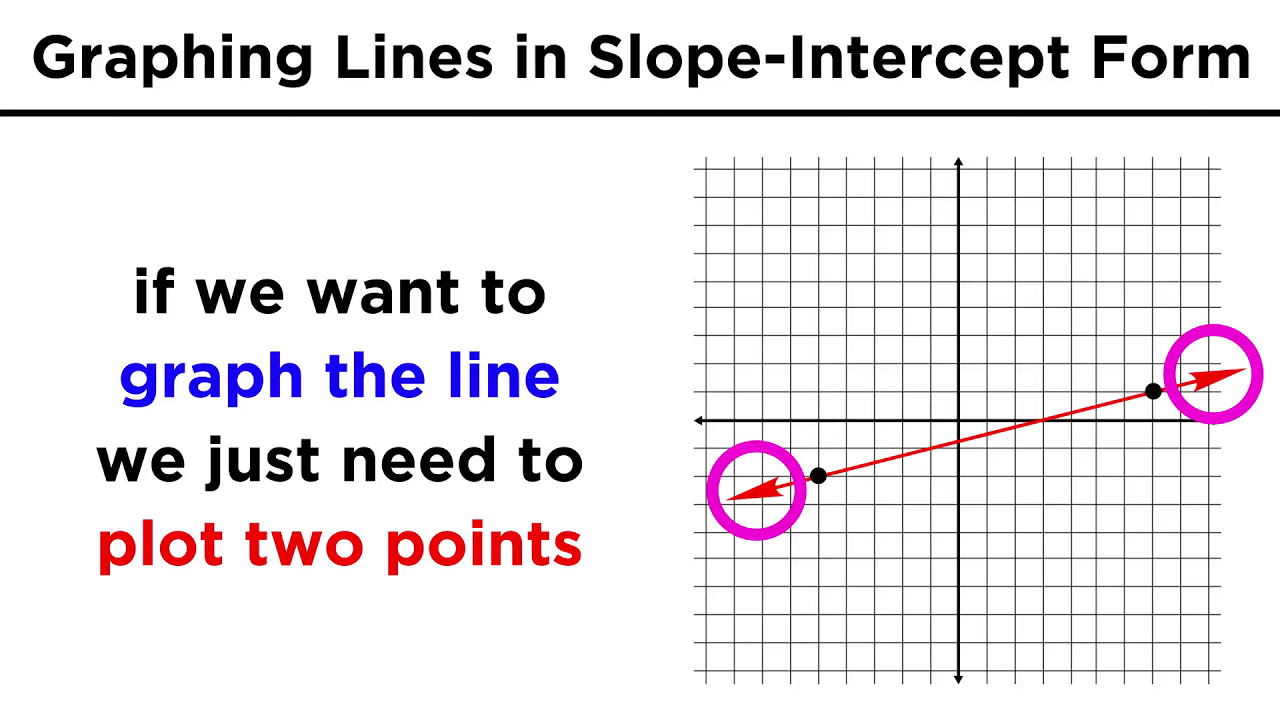
- 👀 The identity function (y = x) is the parent linear function with a slope of 1 and y-intercept at the origin.
- 📊 Linear functions can be written in slope-intercept form (y = mx + b), point-slope form (y - y1 = m(x - x1)), and standard form (ax + by = c).
- 📝 To write a linear function, you need to know the slope (m) and at least one point on the line.
- ✍️ The choice of form to use depends on the information given: slope-intercept form is used when the y-intercept is known, and point-slope form is used with any point and the slope.
- 🔢 When given the slope and a point, you can write the equation of a line in all three forms: slope-intercept, point-slope, and standard form.
- 🎯 The process of finding the equation of a line involves calculating the slope, identifying a point, and then using these to write the function in the desired form.
- 🤔 Dealing with fractions and simplifying equations is an important skill when working with linear functions, especially when the numbers do not work out nicely.
Q & A
What is the main focus of this lesson on linear functions?
-The main focus of this lesson is to review linear functions through the lens of pre-calculus, specifically in preparation for calculus. It emphasizes the importance of understanding derivatives, which are closely related to the slope of a function at a given point.
What is a derivative in calculus?
-In calculus, a derivative is a measure of how a function changes as its input changes. More specifically, it is the slope of the tangent line to the function's graph at a particular point.
How is the slope of a line related to its orientation?
-The slope of a line is a numerical measure of its steepness and orientation. A positive slope indicates that the line is increasing (moving upwards as you move to the right), while a negative slope indicates that the line is decreasing (moving downwards as you move to the right).
What are the different forms of writing linear functions?
-Linear functions can be written in three main forms: slope-intercept form (y = mx + b), point-slope form (y - y1 = m(x - x1)), and standard form (ax + by = c). Each form has its own uses and is applicable in different situations.
What is the identity function in the context of linear functions?
-The identity function is the basic or parent linear function where y equals x. It has a slope of one and passes through the origin, meaning it has a y-intercept at zero.
How can you find the slope of a line without using two points?
-You can find the slope of a line by using the change in y values (the rise) and the change in x values (the run) between any two points on the line. The slope (m) is calculated as the rise over the run, or m = (change in y) / (change in x).
What is the process of converting a linear function from point-slope form to slope-intercept form?
-To convert a linear function from point-slope form (y - y1 = m(x - x1)) to slope-intercept form (y = mx + b), you substitute the given values for m, x1, and y1, and then simplify the equation by distributing the slope and adding or subtracting as necessary to isolate y on one side.
Why is it important to be able to write linear functions in different forms?
-Being able to write linear functions in different forms is important because it allows for flexibility and adaptability in solving various mathematical problems. Different forms may be more convenient or required depending on the context or the specific problem at hand.
What is the significance of the y-intercept in the slope-intercept form of a linear function?
-The y-intercept in the slope-intercept form (y = mx + b) is the point where the line crosses the y-axis. It is a key characteristic of the line and provides information about the starting point of the function on the y-axis.
How do you find the standard form of a linear function from the slope-intercept form?
-To find the standard form (ax + by = c) of a linear function from the slope-intercept form (y = mx + b), you can rearrange the equation by moving all terms involving x and y to one side and making the constant term the other side. Ensure that there are no fractions and the coefficients are integers.
What is the role of the slope in finding derivatives in calculus?
-The slope plays a crucial role in finding derivatives in calculus because the derivative of a function at a specific point is essentially the slope of the tangent line to the graph of the function at that point. Understanding and calculating slope is fundamental to working with derivatives.
Outlines
📘 Introduction to Linear Functions and Calculus
This paragraph introduces the topic of linear functions, emphasizing their importance in the context of pre-calculus and their role in preparing for calculus. The speaker explains that while the work with linear functions remains the same, the perspective shifts to understanding how these functions relate to calculus, particularly through the concept of derivatives. Derivatives are informally described as the slope of the tangent line to a function's graph at a given point. The paragraph sets the stage for a deeper exploration of the relationship between linear functions and calculus.
📔 Understanding Slope and Linear Function Forms
The second paragraph delves into the concept of slope, denoted by the letter M, as a measure of a line's steepness and orientation. The speaker discusses how slope can be determined by the rise over run method, using two points on a graph. The paragraph also outlines different forms of linear functions: the identity function, slope-intercept form (y = mx + b), point-slope form (y - y1 = m(x - x1)), and standard form (ax + by = c). The focus is on the slope-intercept and point-slope forms for writing linear functions, as these are most relevant for calculus. The need to convert between these forms is also highlighted.
📒 Writing Linear Functions with Given Information
This paragraph demonstrates how to write the equation of a line in all three forms when given specific information, such as the slope (m) and y-intercept (b). The process involves plugging the given values into the slope-intercept form, then using the slope and a point to write the point-slope form. The standard form is derived by rearranging the slope-intercept form. The speaker emphasizes that while the given m and b make writing the linear function straightforward, other scenarios might require more work.
📕 Using Graph Information to Write Linear Functions
The fourth paragraph illustrates how to use a graph to find the slope and y-intercept, and then write the equation of the line in all three forms. The process involves identifying points on the graph, calculating the slope using the rise over run method, and then using this information to write the slope-intercept and point-slope forms. The standard form is obtained by rearranging the slope-intercept form, and the speaker notes the importance of ensuring there are no fractions in the standard form.
📗 Writing Linear Functions with Points and Slope
In this paragraph, the speaker shows how to write the equation of a line when given two points through which the line passes. The process starts with calculating the slope using the two points, then writing the point-slope form using one of the points and the calculated slope. The slope-intercept form is derived by simplifying the point-slope form, and the standard form is obtained by rearranging the slope-intercept form. The speaker emphasizes the importance of handling fractions when they appear in the calculations.
📙 Dealing with Fractions in Linear Functions
The final paragraph addresses the challenge of working with fractions when writing linear functions. The speaker demonstrates how to calculate the slope given two points and how to handle the resulting fractions. The process involves writing the point-slope form with fractions, simplifying to obtain the slope-intercept form, and then rearranging to get the standard form without fractions. The speaker shows how to clear fractions by multiplying through by the least common denominator, resulting in an integer coefficient for the standard form.
Mindmap
Keywords
💡Linear Functions
💡Derivatives
💡Slope
💡Tangent Line
💡Slope-Intercept Form
💡Point-Slope Form
💡Standard Form
💡Y-Intercept
💡Rise Over Run
💡Calculus
💡Transformations
Highlights
Linear functions are fundamental to understanding calculus, particularly in finding derivatives.
Derivatives in calculus represent the slope of the tangent line to a function at a given point.
Slope is a measure of a line's steepness and orientation, with positive slopes indicating an increase and negative slopes indicating a decrease.
The identity function, y=x, serves as the parent linear function with a slope of one and passes through the origin.
Linear functions can be written in slope-intercept form (y = mx + b), point-slope form (y - y1 = m(x - x1)), and standard form (ax + by = c).
Slope-intercept form visually presents the slope (m) and y-intercept (b) of a line.
Point-slope form uses a specific point on the graph (x1, y1) and the slope (m) to define a line.
Standard form is often rearranged from other forms and requires integer coefficients for x and y.
Writing linear functions requires knowledge of the slope (m) and at least one point on the line.
Different scenarios may require using different forms of linear functions based on the information provided.
The ability to convert between forms of linear functions is crucial for advanced mathematical work, including calculus.
The process of finding the equation of a line involves identifying key components like the slope and intercepts.
When given specific values for m and b, directly applying them into the slope-intercept form is the most straightforward approach.
If a graph is provided, identifying two points on the line allows for calculating the slope and writing the equation in different forms.
Dealing with fractions and converting them into whole numbers is an essential skill when working with linear functions and calculus.
Clearing fractions by multiplying through by the least common denominator is a common technique to simplify linear equations.
The ability to write linear functions in all three forms is vital for success in calculus, especially when finding derivatives.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: