Tensors for Beginners 2: Vector definition
TLDRThis video explores the concept of vectors, distinguishing between their components and their geometrical essence. It clarifies that vectors are not just lists of numbers but have a deeper meaning, introducing the idea of vectors as arrows in space for a more intuitive understanding. The video also introduces the formal definition of a vector as a member of a vector space, which involves a set of vectors, scalars, and rules for addition and scaling. The script discusses how vectors transform under different coordinate systems, highlighting the peculiar relationship between forward and backward transformations for basis vectors versus their components.
Takeaways
- 📚 Vectors are often defined as lists of numbers or one-dimensional arrays, but this definition is simplistic and doesn't capture the full essence of vectors.
- 🔍 The geometric interpretation of a vector is like an arrow, emphasizing the vector's direction and magnitude, which is more than just a list of numbers.
- ➕ Vector addition can be visualized as placing the tail of one vector at the tip of another, resulting in a new vector that represents the sum of the two.
- 🔢 Scalar multiplication involves scaling a vector by a constant factor, which can be visualized as stretching or compressing the vector while maintaining its direction.
- 🚫 It's important to distinguish between a vector and its components, as components change with different coordinate systems, unlike the invariant nature of vectors themselves.
- 🏷 The most abstract definition of a vector is as a member of a vector space, which includes a set of vectors, scalars, addition rules, and scaling rules.
- 📐 Vector spaces allow for the application of vector operations even to abstract entities that cannot be visualized as arrows, expanding the concept of vectors beyond physical representations.
- 🌐 The script introduces the concept of coordinate transformations and how they relate to vectors, with the forward and backward transformations affecting components differently than basis vectors.
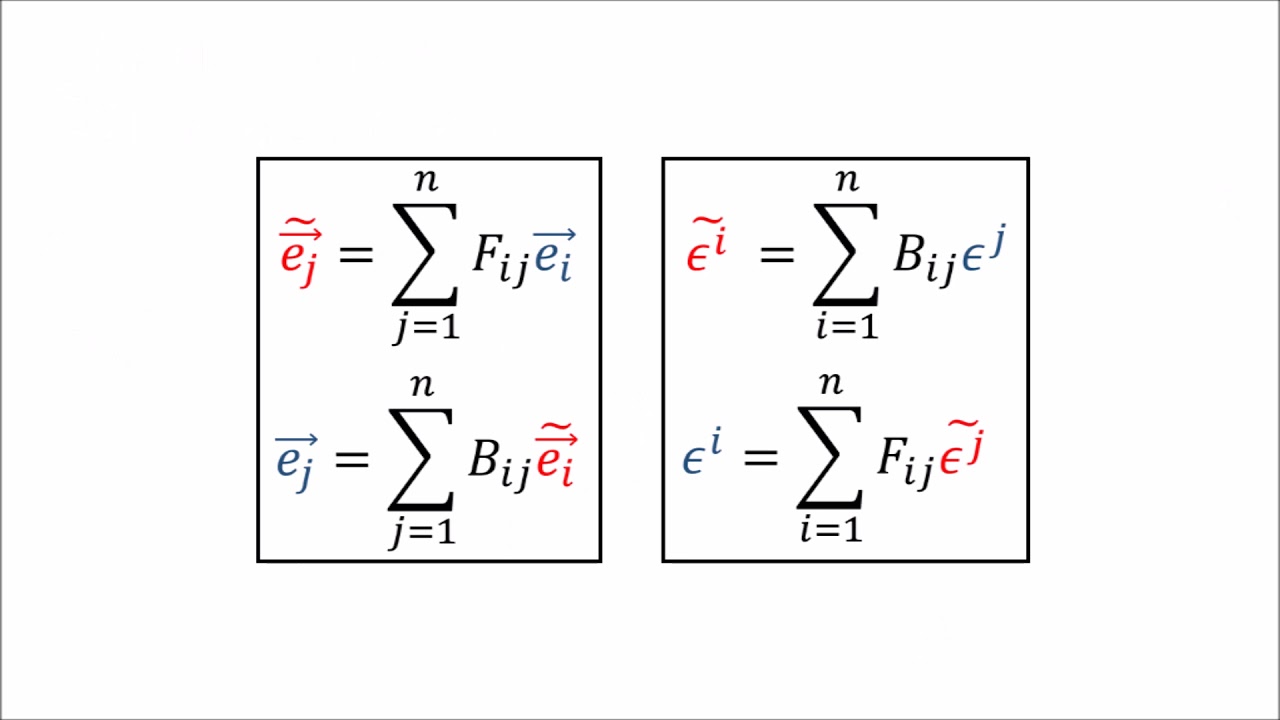
- 🔄 The forward transformation matrix is used to convert components from the old basis to the new basis, while the backward transformation is used to convert from the new basis to the old.
- 🤔 The script hints at a deeper explanation for why the forward and backward transformations affect vector components in the opposite way they affect basis vectors, which will be explained in a subsequent video.
- 📈 For practical purposes, the video series will primarily focus on Euclidean vectors, which are easy to visualize and work with, although it acknowledges that not all vectors are Euclidean.
Q & A
What is the first definition of a vector mentioned in the video?
-The first definition of a vector mentioned is that a vector is a list of numbers or a one-dimensional array of numbers.
How is vector addition performed with the list definition?
-Vector addition with the list definition is performed by adding the corresponding elements of the two vectors to get the new vector with elements V_i + W_i, where i is the index of the elements.
What is the problem with considering a list of numbers as a vector?
-The problem is that a list of numbers actually represents the components of a vector, not the vector itself. Vectors are invariant under a change of coordinates, whereas their components are not.
What is the second definition of a vector presented in the video?
-The second definition is that a vector is like an arrow, a geometric object that can be visualized without the need for a coordinate system.
How is vector addition performed geometrically using the arrow interpretation?
-Geometrically, vector addition is performed by placing the tail of the second vector on the tip of the first vector, creating a 'tip-to-tail' addition, resulting in a vector that goes from the initial point of the first vector to the final point of the second vector.
What is the third definition of a vector presented in the video?
-The third definition states that a vector is a member of a vector space, which is a collection of vectors, scalars, an addition rule, and a scaling rule.
What is a vector space according to the third definition?
-A vector space is a set that includes vectors, scalars, an addition rule to combine vectors, and a scaling rule to change the size of vectors using scalars.
Why is the arrow interpretation of vectors considered limited?
-The arrow interpretation is limited because not all vectors can be visualized as arrows; it only applies to a special kind of vector called a Euclidean vector.
What is the significance of the forward and backward transformations in the context of changing coordinates?
-The forward and backward transformations allow us to move between different coordinate systems and determine how the components of a vector change when measured in different bases.
How do the forward and backward transformations relate to vector components when changing coordinates?
-When changing coordinates, the forward transformation is used to convert new basis components to old basis components, and the backward transformation is used to convert old basis components to new basis components.
What is the reason for the apparent discrepancy in the direction of transformations for basis vectors and their components?
-The discrepancy makes sense because basis vectors transform in the direction of the change (forward to new or backward to old), while components transform in the opposite direction (forward from new to old or backward from old to new), ensuring consistency in vector representation across coordinate systems.
Outlines
📚 Introduction to Vectors and Their Definitions
This paragraph introduces the concept of vectors, presenting two different definitions. The first definition describes a vector as a list or one-dimensional array of numbers, with examples provided to illustrate vector addition and scaling. However, it is noted that this definition is limited as it only considers the components of a vector, not the vector itself. The second definition likens a vector to an arrow in space, emphasizing its geometric nature and invariance under coordinate transformations. Vector addition and scaling are also discussed in this geometric context, highlighting the parallelogram rule for addition and the effect of scaling on the vector's magnitude and direction. The paragraph concludes by pointing out that not all vectors can be represented as arrows, indicating the existence of other types of vectors beyond Euclidean vectors.
🔍 The Abstract Concept of Vector Spaces
The second paragraph delves into the abstract definition of a vector as a member of a vector space, which is a mathematical structure comprising four elements: a set of vectors, a set of scalars, an addition rule, and a scaling rule. This definition is devoid of specific numbers or visual representations, focusing instead on the rules that govern vector operations. The paragraph explains that while this definition may seem abstract, it is powerful because it allows for the application of vector rules to a wide range of mathematical entities that can be added and scaled, even if they cannot be visualized as arrows. The discussion also touches on the behavior of vectors under a change of coordinates, using the concepts of 'old basis' and 'new basis' to illustrate how vectors can be expressed in different coordinate systems. The paragraph concludes with an exploration of how the components of a vector are related to each other when transformed from one basis to another, introducing the forward and backward transformations and their roles in this process.
Mindmap
Keywords
💡Tensor
💡Vector
💡Vector Addition
💡Scaling
💡Components
💡Euclidean Vector
💡Vector Space
💡Coordinate System
💡Basis
💡Transformation
Highlights
Introduction to the concept of tensors with a focus on vectors as the first example.
Definition of a vector as a list of numbers or a one-dimensional array.
Explanation of vector addition by adding corresponding elements of two vectors.
Description of scaling vectors using a scaling constant.
Clarification that lists of numbers are vector components, not vectors themselves.
Vectors are invariant under a change of coordinates, unlike their components.
Vectors as geometrical objects with inherent meaning beyond numerical components.
Second definition of a vector as an arrow in space, emphasizing its geometric nature.
Geometric method of vector addition through 'tip-to-tail' placement.
Visualization of vector addition as creating a parallelogram.
Scaling vectors as arrows by changing length while maintaining direction.
Limitation of the arrow interpretation for vectors that cannot be visualized as arrows.
Introduction to the concept of Euclidean vectors as a special type of vector.
Third definition of a vector as a member of a vector space, involving a set of rules.
Components of a vector space including vectors, scalars, addition, and scaling rules.
Abstract nature of the vector space definition and its broad applicability in mathematics.
Discussion on how vectors behave under a change of coordinates and the importance of basis.
Demonstration of expressing a vector in terms of different bases and writing it as a linear combination.
Illustration of vector components in both old and new bases as column vectors.
Misapplication and correction of using forward and backward transformations on vector components.
Revelation that forward transformations apply backward to components and vice versa.
Promise of an explanation for the observed behavior of vector components in the next video.
Transcripts
Browse More Related Video

Linear combinations, span, and basis vectors | Chapter 2, Essence of linear algebra
Tensors for Beginners 6: Covector Transformation Rules

Tensor Calculus 5: Derivative Transformation Rules (Contravariance)
Tensors for Beginners 4: What are Covectors?
Tensors for Beginners 5: Covector Components (Contains diagram error; see description)

Tensors for Beginners 1: Forward and Backward Transformations (REMAKE)
5.0 / 5 (0 votes)
Thanks for rating: