Tensors for Beginners 5: Covector Components (Contains diagram error; see description)

eigenchris
14 Dec 201708:48
EducationalLearning
32 Likes 10 Comments

TLDRThis video delves into the concept of covector components, explaining how they function as linear functions from vectors to numbers, forming a vector space known as V*. Covectors are invariant geometric objects, but their components vary with coordinate systems. The video introduces the 'dual basis', epsilon covectors, which project vector components and form the basis for the dual space V*. It visually represents covectors as stacks of planes and demonstrates how to express any covector as a linear combination of the dual basis, highlighting the process of changing covector bases and the relationship between old and new components.

Takeaways
  • 📚 Covectors are functions that map vectors to numbers and are part of a vector space known as V*.
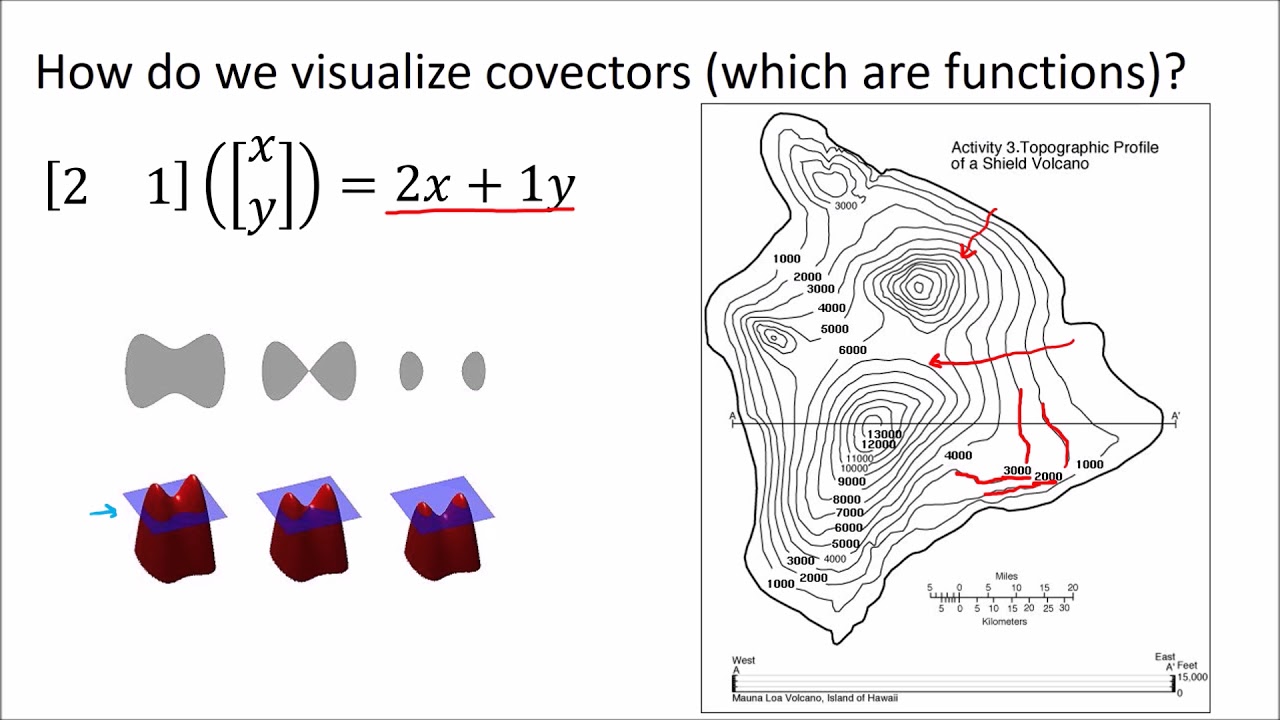
  • 🔍 Covectors can be visualized as oriented stacks of planes and are similar to row vectors in representation.
  • 🌐 Covectors are invariant geometric objects, independent of the coordinate system, while their components depend on the chosen coordinate system.
  • 🔢 The components of a covector are represented by row vectors, which indicate how the covector interacts with basis vectors in a given space.
  • 📏 The dual basis covectors, epsilon^1 and epsilon^2, are defined such that they project out the components of a vector when applied to it.
  • 🎯 The Kronecker Delta is used to express the interaction between the dual basis covectors and the basis vectors of the vector space.
  • 📈 The visual representation of the epsilon covectors shows them as projections that extract the components of a vector in a given basis.
  • 🧩 Any covector can be expressed as a linear combination of the dual basis covectors, demonstrating the concept of a basis in the dual space V*.
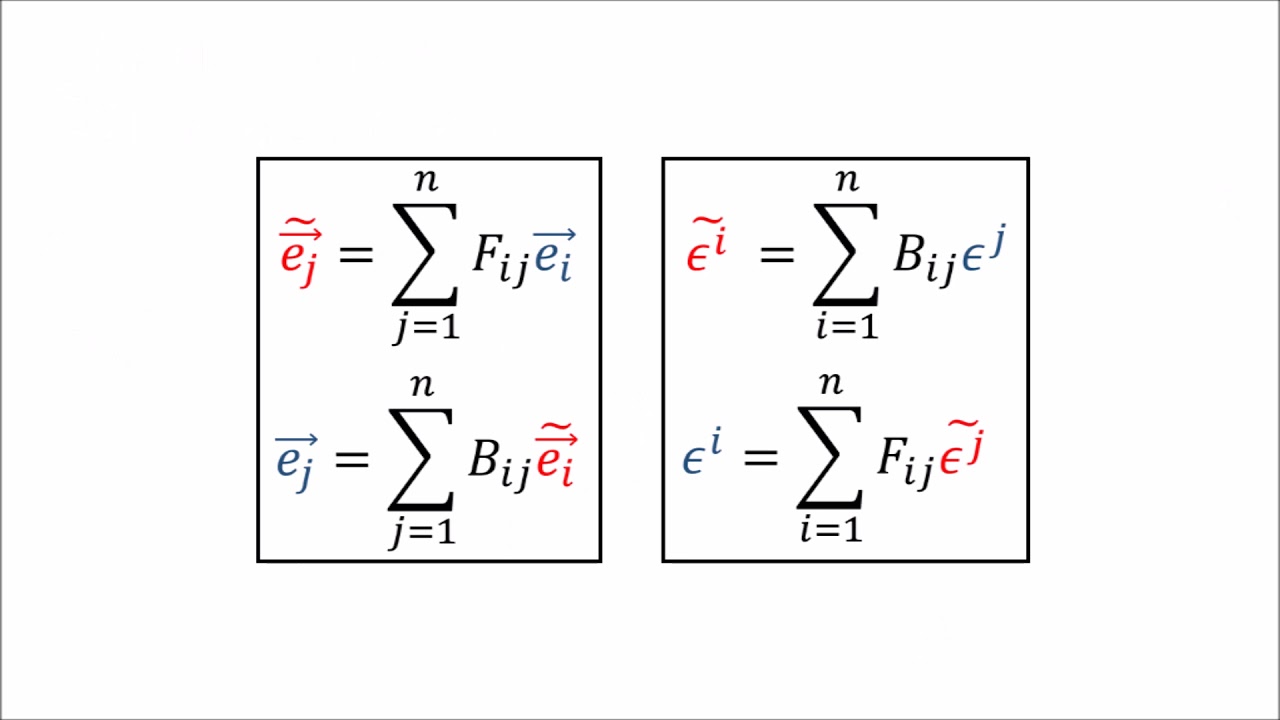
  • 🔄 The process of changing the basis for a covector involves applying the covector to new basis vectors and calculating the new components.
  • 🔄🔄 The transformation between different covector bases is analogous to a change of basis in vectors, but with the roles of forward and backward transformations reversed.
  • 📉 The components of a covector in one basis can be converted to another basis using matrix multiplication, reflecting the relationship between the old and new components.
Q & A

  • What is a covector?

    -A covector is a function that takes vectors as inputs and produces numbers as outputs. It is linear and obeys certain properties, allowing them to form a vector space known as V*.

  • How are covectors visualized?

    -Covectors can be visualized as oriented stacks of planes, which are geometric objects that do not depend on a coordinate system.

  • What is the relationship between row vectors and covector components?

    -Row vectors represent the components of a covector in a given basis, similar to how column vectors represent the components of a vector in a basis.

  • Why are covector components dependent on the coordinate system?

    -Covector components depend on the coordinate system because they represent the projection of a covector onto the basis vectors of a chosen coordinate system.

  • What are the epsilon covectors?

    -The epsilon covectors, denoted as epsilon^1 and epsilon^2, are special covectors that act as a dual basis for the vector space V, allowing us to express any covector as a linear combination of these epsilons.

  • How do epsilon covectors project vector components?

    -When an epsilon covector is applied to a vector, it projects out the corresponding component of the vector in the basis it is associated with.

  • What is the Kronecker Delta and how is it related to epsilon covectors?

    -The Kronecker Delta is a function that returns 1 if its two indices are equal and 0 otherwise. It is used to define the action of epsilon covectors on basis vectors.

  • How can a general covector be expressed in terms of the epsilon covectors?

    -A general covector can be written as a linear combination of the epsilon covectors, with the coefficients of this combination being the components of the covector in the dual basis.

  • What is the significance of the dual basis in the context of covectors?

    -The dual basis, represented by the epsilon covectors, is significant because it forms a basis for the set of all covectors, allowing us to express any covector in terms of this basis.

  • How do changes in the vector basis affect the covector components?

    -Changes in the vector basis lead to changes in the covector components due to the linearity of covectors. The new covector components can be found by applying the covector to the new basis vectors.

  • What is the difference between the forward and backward transformation of covector components under a change of basis?

    -The forward transformation of covector components brings us from the old basis to the new basis, while the backward transformation brings us from the new basis to the old basis. This is the opposite of what happens with vector components under a change of basis.

  • Why can't we simply flip column vectors on their side to get row vectors?

    -Flipping column vectors on their side to get row vectors does not work in general because covector components are measured by counting the number of covector lines that the basis vector pierces, which is not equivalent to the number of basis vectors used in the construction of a vector.

Outlines
00:00
📚 Introduction to Covector Components

This paragraph introduces the concept of covector components, emphasizing that covectors are linear functions taking vectors to numbers, forming a vector space known as V*. The paragraph explains the geometric nature of covectors and their invariance, contrasting with the dependency of covector components on the coordinate system. It also highlights the analogy between row vectors and covector components, setting the stage for a deeper exploration of how covectors can be represented and manipulated in different coordinate systems. The introduction of special covectors, epsilon^1 and epsilon^2, as functions from vectors to numbers, is used to illustrate the projection of vector components in a given basis.

05:04
🔍 The Dual Basis and Covector Representation

The second paragraph delves into the dual basis concept, explaining how the epsilon covectors form a basis for the set of all covectors, hence the term 'dual basis'. It visually represents the process of determining covector components by applying a covector to basis vectors and counting the number of lines intersected. The paragraph further discusses the algebraic expression of any covector as a linear combination of the dual basis, illustrating the process with an example of a covector 'alpha'. It also touches on the flexibility of choosing different bases to express a covector, introducing the concept of epsilon tildes as an alternative dual basis. The summary concludes with an exploration of how covector components transform under a change of basis, contrasting this with the process for vector components and emphasizing the unique nature of covector components as measured by the number of covector lines pierced by a basis vector.

Mindmap
Keywords
💡Covectors
Covectors, also known as one-forms, are abstract mathematical objects that take vectors as inputs and produce scalars as outputs. They are linear functions, meaning they preserve the operations of vector addition and scalar multiplication. In the video, covectors are discussed in the context of their components and how they form a vector space denoted as V*. The script uses the analogy of row vectors to explain covector components, emphasizing that while covectors themselves are invariant geometric objects, their components vary with the choice of coordinate system.
💡Vector Space
A vector space, in linear algebra, is a collection of objects called vectors, which can be added together and multiplied by scalars (from a field such as the real numbers), satisfying a set of axioms including commutativity, associativity, identity, and distributivity. In the script, the vector space V* is mentioned as the space formed by covectors, which obeys the properties that allow for addition and scaling of covectors.
💡Linearity
Linearity refers to the property of a function that allows it to distribute over vector addition and scalar multiplication. In the context of the video, the linearity of covectors is fundamental because it ensures that the operations on vectors are preserved when applying the covector function. This property is what allows covectors to form a vector space.
💡Components
Components are the scalar values that describe the position of a vector or covector in a given basis. In the script, the concept of covector components is introduced as the scalars that result from the action of a covector on basis vectors. The script explains how row vectors can be thought of as representing the components of a covector in a specific coordinate system.
💡Coordinate System
A coordinate system is a reference framework for defining positions and transformations in a geometric space. The video script highlights that covector components are dependent on the chosen coordinate system, meaning that the representation of a covector can change if a different coordinate system is used.
💡Dual Space
The dual space, denoted as V*, is the vector space consisting of all linear functionals (covectors) on a given vector space V. In the script, the dual space is discussed in relation to the covectors and how they can be visualized and manipulated within this space.
💡Basis
A basis is a set of vectors in a vector space that are linearly independent and span the entire space. In the video, a basis for the vector space V is introduced, and it is used to define the dual basis for the covector space V*. The script explains how the basis vectors of V interact with the dual basis vectors of V* to determine covector components.
💡Kronecker Delta
The Kronecker Delta is a function that equals 1 if its two indices are equal and 0 otherwise. In the script, the Kronecker Delta is used to define the action of the dual basis covectors epsilon^i on the basis vectors e_j, illustrating the selection of components in a covector.
💡Dual Basis
The dual basis is a set of covectors that correspond to a given basis of a vector space, such that each covector in the dual basis selects a component of a vector when applied to it. In the video, the epsilon covectors are introduced as the dual basis for the vector space V, allowing for the expression of any covector as a linear combination of these dual basis elements.
💡Linear Combination
A linear combination is an expression constructed from a set of vectors by multiplying each vector by a scalar and adding the results. In the script, linear combinations are used to express vectors in terms of their basis and to represent covectors as combinations of the dual basis elements.
💡Change of Basis
A change of basis is the process of expressing vectors or covectors in terms of a different basis set. The script discusses how covector components transform under a change of basis, using the example of transitioning from one dual basis to another, and how this transformation is represented by a matrix.
Highlights

Covector components are discussed as part of the ongoing series on covectors.

Covector functions take vectors to produce numbers and are linear, forming a vector space known as V*.

Covector components are visualized as oriented stacks of planes.

Row vectors are analogous to covector components, unlike column vectors which represent vector components.

Covectors are invariant geometric objects, independent of coordinate systems, whereas their components depend on the chosen system.

The concept of covector components is introduced in relation to the linear combination of basis vectors.

Special covectors epsilon^1 and epsilon^2 are introduced as functions from vectors to numbers, defining the dual basis.

The Kronecker Delta is used to define the action of epsilon covectors on basis vectors.

The epsilon covectors are shown to project out vector components when applied to a vector.

The visual representation of epsilon covectors as stacks of lines is explained.

A general covector 'alpha' is expressed as a linear combination of the epsilon covectors, defining the dual basis for the space V*.

The process of obtaining covector components by applying a covector to basis vectors is illustrated.

Different bases can be used to express a covector, such as the epsilon tildes, offering alternative dual bases.

The transformation of covector components under a change of basis is discussed, highlighting the matrix relationship.

The distinction between vector and covector components in terms of their construction and measurement is clarified.

The unique behavior of vector and covector components in an orthonormal basis is explained, where both have the same representation.

The practical application of the theory is demonstrated through the example of transforming covector components between different dual bases.

Transcripts

Browse More Related Video

Tensors for Beginners 6: Covector Transformation Rules

Tensors for Beginners 4: What are Covectors?

Tensors for Beginners 16: Raising/Lowering Indexes (with motivation, sharp + flat operators)

Tensor Calculus 8: Covector Field Transformation Rules (Covariance)

Tensors for Beginners 3: Vector Transformation Rules

Tensors for Beginners 2: Vector definition

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CovectorsLinear AlgebraVector SpaceDual BasisKronecker DeltaGeometric ObjectsCoordinate SystemsLinear FunctionsBasis TransformationEducational ContentMathematics Tutorial