Tensors for Beginners 4: What are Covectors?
TLDRThis script explores the concept of covectors, introducing them as linear functions that map vectors to scalars. It clarifies the distinction between row and column vectors, especially outside of an orthonormal basis, and illustrates how to visualize covectors as stacks of lines. The video demonstrates the linear properties of covectors, including how they can be scaled and added, and introduces the dual space 'V*' where covectors follow distinct addition and scaling rules. The visualization technique using lines allows for an intuitive understanding of how a covector acts on a vector by simply counting the lines pierced by the vector.
Takeaways
- 📚 Tensors are mathematical objects with specific transformation properties; vectors are the first example of tensors, and they are contravariant.
- 🔄 Covectors, the second example of tensors, are fundamentally different from row and column vectors, especially outside of an orthonormal basis.
- 🔢 Covectors can be thought of as functions that take a vector input and return a scalar output, demonstrated through the concept of dot products.
- 📉 The visualization of covectors involves thinking of them as stacks of lines, similar to contour lines on a topographic map, indicating constant values.
- ↗️ The direction of increase for a covector is indicated by the orientation of the stack of lines, which is perpendicular to the vector it acts upon.
- 🔍 The value of a covector acting on a vector can be determined by counting how many lines of the stack the vector pierces through.
- 📈 The density of the stack of lines in the visualization of a covector corresponds to the magnitude of the scalar output when acting on a vector.
- 🔄 Linearity in covectors is characterized by the ability to add inputs or outputs and scale inputs or outputs without changing the result.
- 🧩 Covectors can be modified by scaling, which involves adjusting the density of the stack of lines, and adding, which combines the densities of multiple covectors.
- 🌐 The set of all covectors that act on a vector space V forms a new vector space called the dual space, denoted as V*, with its own set of addition and scaling rules.
- 📝 The dual space V* has elements that are linear functions from V to the real numbers, and these functions follow specific rules for addition and scaling, distinct from those of V.
Q & A
What is the primary difference between a vector and a covector?
-A vector is an element of a vector space, often visualized as an arrow with direction and magnitude. A covector, on the other hand, is a function that takes a vector as input and produces a scalar as output, exhibiting linearity in its operations.
Why are column vectors and row vectors considered fundamentally different types of objects?
-Column vectors and row vectors are fundamentally different because they transform in different ways under changes of basis. This difference is typically obscured in an orthonormal basis, but becomes apparent in other coordinate systems.
How can we visualize a covector?
-A covector can be visualized as a stack of lines, where each line represents a constant value of the function represented by the covector. The orientation of the stack indicates the direction of increase.
What is the significance of the dot product in the context of covectors?
-The dot product is used to compute the output value when a covector (visualized as a row vector) acts on a vector (visualized as a column vector), demonstrating the linear relationship between the two.
How does the concept of 'linearity' apply to covectors?
-Linearity in the context of covectors means that the covector can add or scale either the inputs or the outputs and still yield the same result. This property is fundamental to the definition of a covector as a linear function.
What is the dual space, and how is it related to covectors?
-The dual space, denoted as V*, is the vector space formed by all covectors that act on the vectors of another vector space V. It has its own set of addition and scaling rules, different from those of V.
How can we determine the value of a covector acting on a vector using the stack visualization?
-By counting the number of lines the vector 'pierces' through in the stack visualization of the covector. The sum of these lines gives the scalar output of the covector acting on the vector.
What happens when we scale a covector?
-When scaling a covector, the density of the stack of lines representing the covector increases or decreases accordingly. A larger covector has a denser stack, while a smaller one has a sparser stack.
How is the addition of two covectors visualized and what is the result?
-The addition of two covectors is visualized by combining their respective stacks of lines, resulting in a new stack that has the combined density of the original covectors in their respective directions.
What is the relationship between the covector and the contravariant transformation of vector components?
-The covector, like the contravariant vector, changes in the opposite way under a change of basis. This is why vectors are said to be contravariant, and it's a key concept in understanding how covectors transform.
Can you provide an example of how to calculate the output of a covector acting on a vector?
-Certainly. Given a row vector (covector) (2, 1) and a column vector (3, -4), the output is calculated as 2*3 + 1*(-4) = 6 - 4 = 2, which is the scalar result of the covector acting on the vector.
Outlines
📚 Introduction to Covectors and Their Linearity
This paragraph introduces the concept of a covector as a function that acts on vectors to produce a scalar, emphasizing their linearity. It explains that while row vectors can be thought of as simple 'flipped' column vectors in an orthonormal basis, they are fundamentally different in other coordinate systems. The paragraph clarifies that covectors are best understood as functions, using the dot product to calculate the output when a covector 'acts' on a vector. The properties of linearity, where inputs or outputs can be added or scaled without changing the result, are highlighted, illustrating the fundamental nature of covectors as linear functions.
📈 Visualizing Covectors with Stacks of Lines
The second paragraph delves into visualizing covectors as stacks of lines, drawing an analogy with topographic maps to represent elevation. It describes how to determine the value of a covector acting on a vector by counting the number of lines pierced by the vector, considering the direction of increase. The paragraph also explores how modifying the density of the stack (scaling the covector) affects the output value, demonstrating the process with examples of doubling and halving the covector's effect. This visualization technique simplifies the understanding of how a covector interacts with a vector without the need for coordinate systems or components.
🔍 Operations on Covectors: Scaling and Addition
The final paragraph discusses the operations that can be performed on covectors, specifically scaling and addition. It explains how to scale a covector by adjusting the density of the stack of lines, which in turn affects the output when the covector acts on a vector. The paragraph also covers the addition of two covectors, creating a new covector with combined directional densities. The concept of the dual space (V*) is introduced, where the set of all covectors forms a vector space with its own unique addition and scaling rules, distinct from those of the original vector space V. The dual space is denoted with different colored rules to emphasize the difference in operations for vectors and covectors.
Mindmap
Keywords
💡Tensor
💡Covector
💡Orthonormal Basis
💡Linearity
💡Dot Product
💡Scalar
💡Contravariant
💡Visualizing Covectors
💡Dual Space
💡Stacks of Lines
💡Vector Space
Highlights
Introduction to the concept of a tensor, specifically the contravariant nature of vectors.
Exploration of the covector as the second example of a tensor, distinct from vectors.
Differentiation between column vectors and row vectors, especially outside of orthonormal bases.
Row vectors conceptualized as functions on column vectors, demonstrated through matrix multiplication.
Generalization of the covector as a function that maps vectors to scalars.
Illustration of the linearity property of row vectors through addition and scaling operations.
Visualization of covectors as stacks of lines, analogous to topographic maps.
Method to determine the value of a covector acting on a vector by counting pierced lines in the stack.
Explanation of how to modify covectors by scaling, affecting the density of the line stacks.
Addition of covectors demonstrated through combining their respective densities.
Introduction of the dual space 'V*' as a vector space formed by all covectors acting on 'V'.
Differentiation between the adding and scaling rules for vectors and covectors.
Clarification on the linearity of covectors and their role as linear functions.
Summary of covectors as functions from vectors to real numbers with specific properties.
Final visualization technique for understanding how a covector acts on a vector without needing coordinate systems.
Transcripts
Browse More Related Video
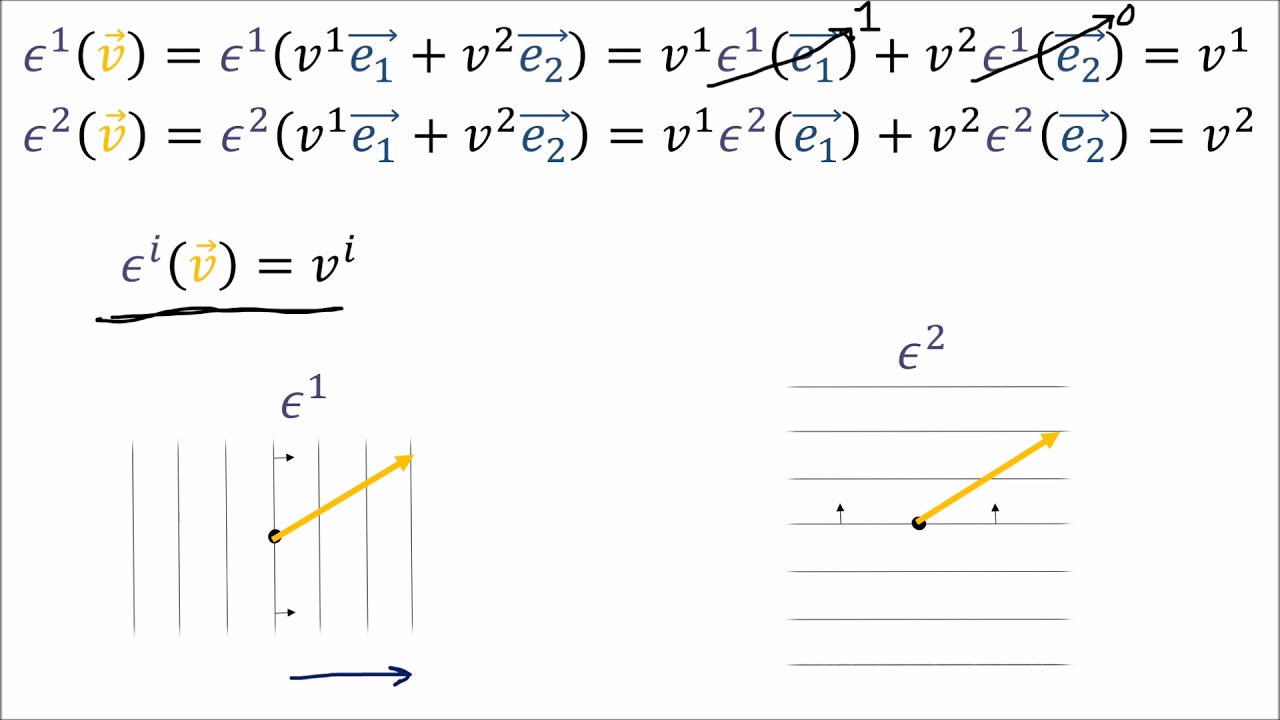
Tensors for Beginners 5: Covector Components (Contains diagram error; see description)
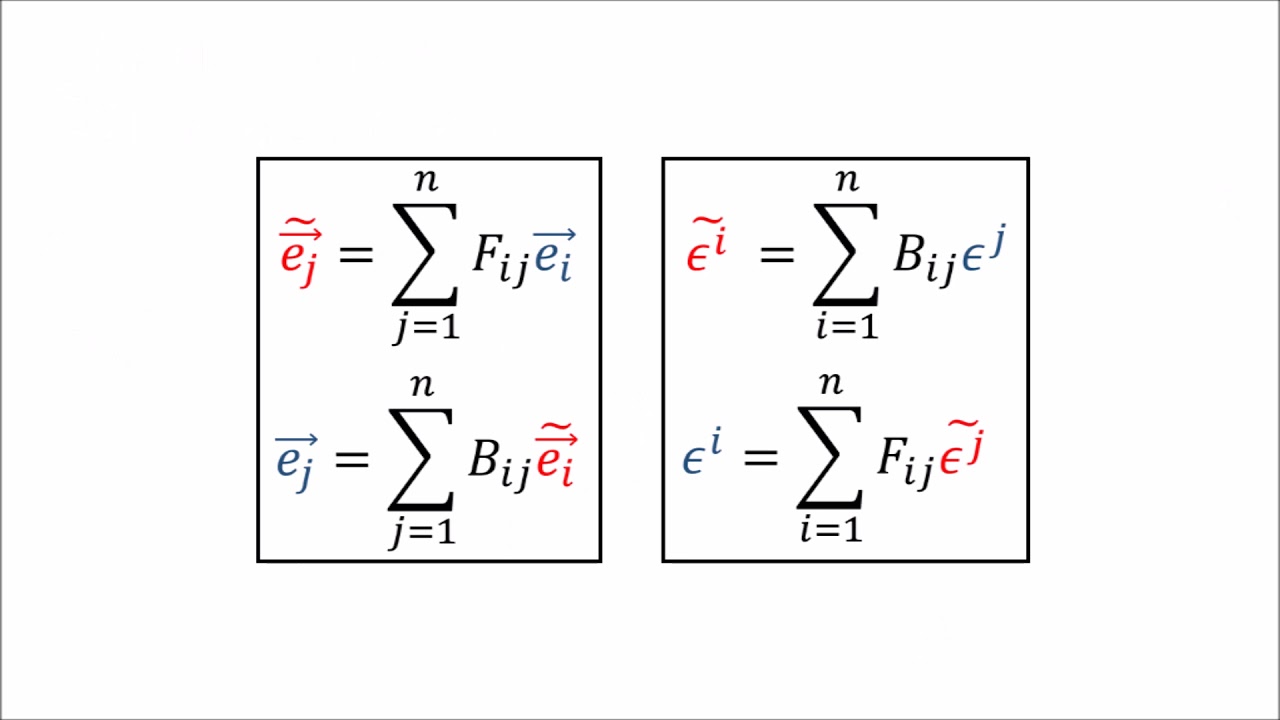
Tensors for Beginners 6: Covector Transformation Rules

Tensors for Beginners 14: Tensors are general vector/covector combinations

Tensors for Beginners 2: Vector definition
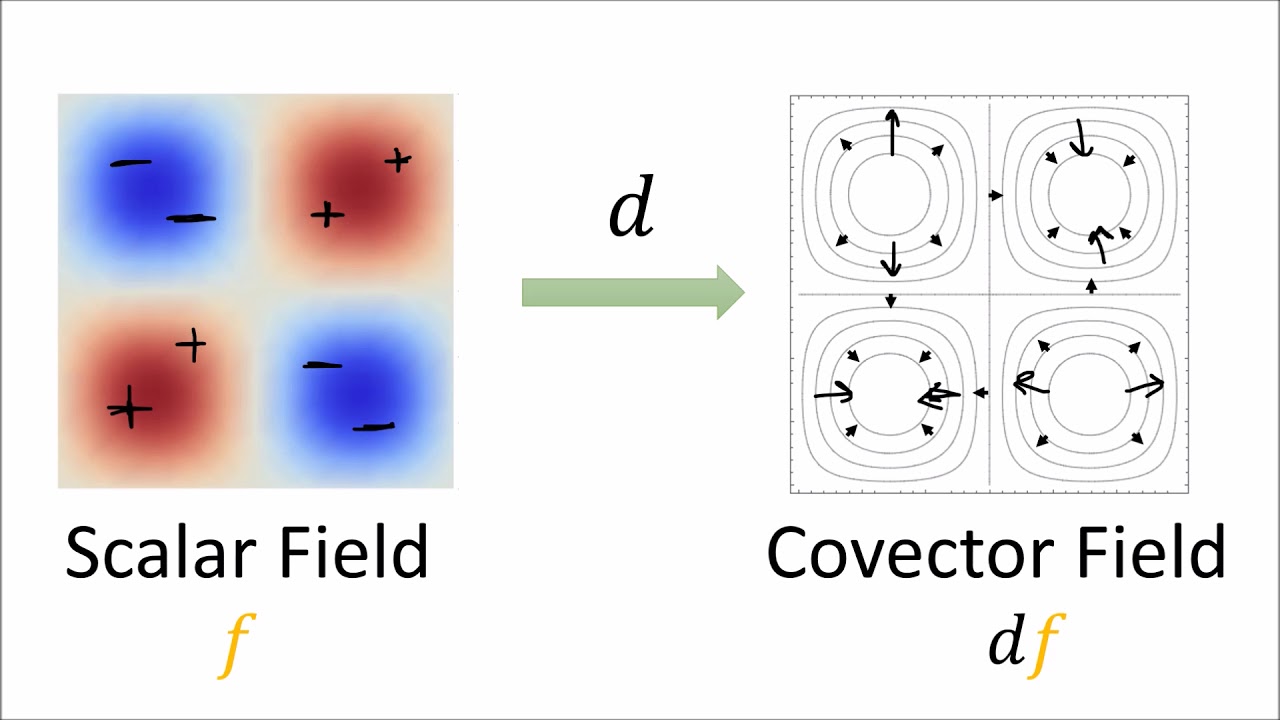
Tensor Calculus 6: Differential Forms are Covectors

Jacobian prerequisite knowledge
5.0 / 5 (0 votes)
Thanks for rating: