Tensor Calculus 5: Derivative Transformation Rules (Contravariance)
TLDRThis educational video delves into the concept of derivatives as vectors, focusing on the contravariant transformation rule. It builds upon the basics of vector transformation rules, illustrating how vectors and their fields can be expressed as linear combinations in various bases. The video employs Einstein summation notation and multivariable chain rule to explain the transformation of vector components, emphasizing their contravariant nature. It also clarifies the distinction between forward and backward transformations for basis vectors and components. Practical examples, including a circular curve, demonstrate the application of these concepts, highlighting the geometric intuition behind vector components' behavior and their contravariance.
Takeaways
- 📚 Derivatives are vectors and understanding their transformation is crucial, especially in the context of contravariant behavior.
- 🔍 The script builds upon the concept of vector transformation rules introduced in the 'Tensors for Beginners' series.
- 🌐 Vectors can be expanded as linear combinations of basis vectors, and the components change depending on the basis set used.
- 📈 Einstein summation notation is used to compactly express the formulas for basis vector expansions.
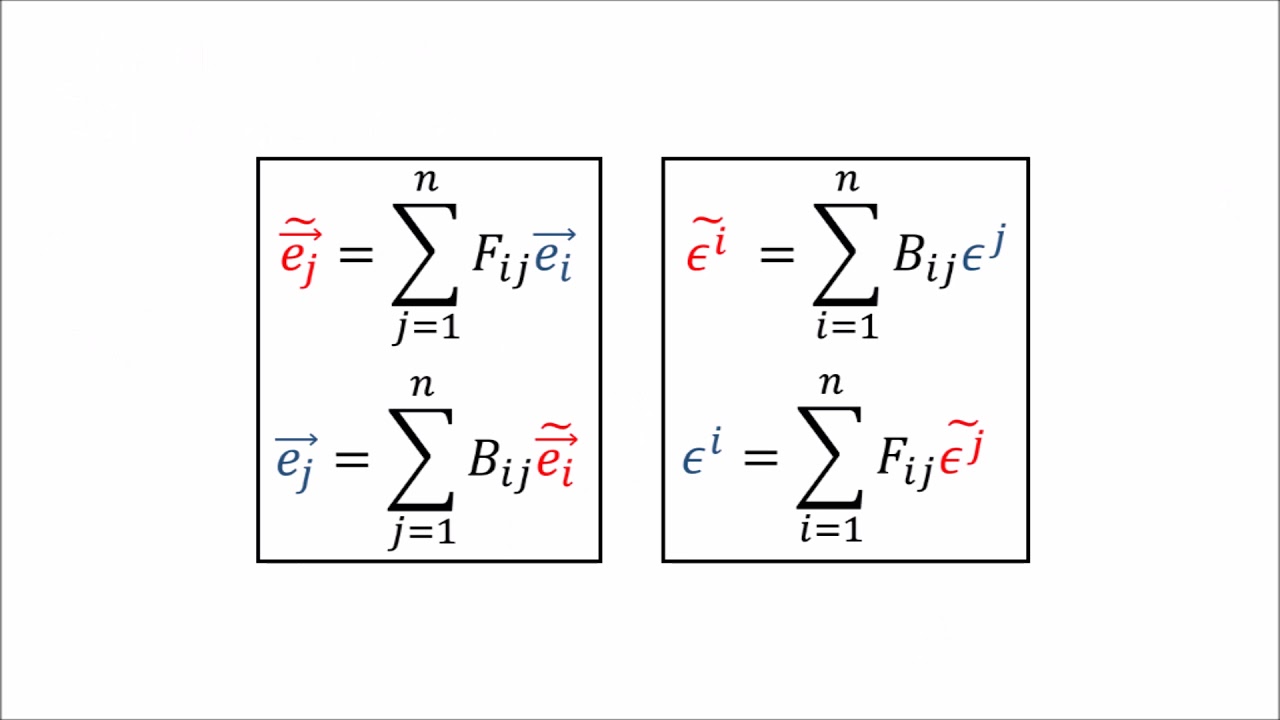
- 🔄 Contravariant transformation is explained through the relationship between old and new basis vectors and their corresponding components.
- 🔢 The transformation of vector components involves multiplying by backward transform coefficients, highlighting their contravariant nature.
- 📉 When basis vectors grow, vector components shrink, which is a geometric interpretation of contravariance.
- 📚 The script explains how to apply these concepts to vector fields of tangent vectors along curves, using both Cartesian and polar basis.
- 🔄 The forward and backward transformations (Jacobian and inverse Jacobian) are key in transforming between different basis vectors.
- 📝 The multivariable chain rule is the foundation for deriving the formulas for transforming vector components.
- 🧩 The script provides a concrete example involving a circular curve to demonstrate the transformation of vector components.
- 🔑 Memorization of formulas is eased by understanding that they stem from the multivariable chain rule, not needing to be memorized individually.
- 🌐 The script concludes by discussing the transition from considering position vectors to derivative operators as basis vectors, which is essential for dealing with curved surfaces and manifolds.
Q & A
What is the main topic discussed in the video?
-The main topic discussed in the video is the concept of derivatives as vectors, specifically focusing on why they are considered contravariant and how they follow the contravariant transformation rule.
Why are derivatives referred to as vectors?
-Derivatives are referred to as vectors because they can be expanded as linear combinations of basis vectors, similar to how vectors are represented in different coordinate systems.
What is the contravariant transformation rule?
-The contravariant transformation rule states that when basis vectors transform one way (using the forward transform), the vector components transform in the opposite way (using the backward transform), hence the term 'contravariant'.
How does the Einstein summation notation simplify the representation of basis vector expansions?
-The Einstein summation notation simplifies the representation of basis vector expansions by compactly expressing the linear combinations of basis vectors in terms of their coordinates, without explicitly writing out the summation signs.
What is the relationship between the forward and backward transform coefficients in the context of vector transformation?
-The forward and backward transform coefficients, denoted by F and B respectively, are used to relate the old and new basis vectors and their components. The forward transform is used to transform basis vectors, while the backward transform is used to transform vector components.
Why do vector components shrink when the basis vectors grow?
-Vector components shrink when the basis vectors grow because the components are contravariant. This means that if the basis vectors are scaled up, the components must scale down to maintain the same vector in the new coordinate system.
How are the components of a tangent vector field transformed from Cartesian to polar coordinates?
-The components of a tangent vector field are transformed from Cartesian to polar coordinates using the backward transform, which involves multiplying the Cartesian components by the inverse Jacobian matrix.
What is the significance of the Jacobian and inverse Jacobian matrices in vector field transformations?
-The Jacobian matrix represents the forward transform (from Cartesian to polar coordinates), while the inverse Jacobian matrix represents the backward transform (from polar to Cartesian coordinates). These matrices are crucial for transforming vector field components between coordinate systems.
Why is it unnecessary to memorize the transformation formulas for vector components?
-It is unnecessary to memorize the transformation formulas for vector components because they can be derived directly from the multivariable chain rule, which is a fundamental concept in calculus.
What is the role of the position vector R in the transformation formulas?
-The position vector R appears in the transformation formulas as part of the parameterization of the coordinate systems. However, the video suggests that in future discussions, the focus will shift from position vectors to partial derivative operators, which can be considered as basis vectors without the need for an origin point.
Why might the concept of position vectors be limiting in the context of curved surfaces and manifolds?
-The concept of position vectors is limiting in the context of curved surfaces and manifolds because these mathematical structures do not necessarily have a well-defined origin point, which is required for position vectors. Using partial derivative operators as basis vectors avoids this limitation.
Outlines
📚 Understanding Derivatives as Vectors and Contravariant Transformation
This paragraph introduces the concept of derivatives as vectors and their contravariant transformation rule. The video builds upon the vector transformation rules from the 'Tensors for Beginners' series, emphasizing the expansion of vectors and vector fields as linear combinations of basis vectors. It explains how the choice of basis vectors affects the components of these vectors and fields. The Einstein summation notation is used to express these expansions compactly. The contravariant nature of vector components is highlighted, showing how they transform in the opposite way to the basis vectors, using forward and backward transformation coefficients. The geometric interpretation of this contravariance is also discussed, where increasing the size of the basis vectors results in a decrease in the vector components.
🔍 Expanding on Contravariant Vector Components and Multivariable Chain Rule
The second paragraph delves deeper into the contravariant transformation of vector components, illustrating how they are derived from the multivariable chain rule. It clarifies that the transformation of vector components is the inverse of the basis vector transformation, hence the term 'contravariant.' The paragraph provides a practical example of transforming vector components from Cartesian to polar coordinates using the backward (inverse Jacobian) matrix, confirming the correctness of the transformation through matrix multiplication. The forward (Jacobian) matrix is also discussed for the reverse transformation. The video emphasizes that understanding the multivariable chain rule is key to grasping these transformations, negating the need for memorization of formulas.
🌐 Transitioning from Position Vectors to Partial Derivative Operators as Basis Vectors
The final paragraph discusses a conceptual shift from considering position vectors as basis vectors to using partial derivative operators for the same purpose. It explains that these operators can be treated as vectors due to their ability to be scaled and combined in linear combinations, and because they have directionality associated with them. The paragraph clarifies that this approach removes the need for an origin point, which is beneficial when dealing with curved surfaces and manifolds. The video concludes by reinforcing the idea that vector field components are contravariant and that all transformation formulas are derived from the multivariable chain rule, simplifying the understanding of these concepts.
Mindmap
Keywords
💡Derivatives
💡Vectors
💡Basis Vectors
💡Contravariant Transformation Rule
💡Einstein Summation Notation
💡Chain Rule
💡Jacobian
💡Inverse Jacobian
💡Tensors
💡Multivariable Chain Rule
💡Partial Derivative
Highlights
Derivatives are introduced as vectors and their contravariant transformation rule is explained.
The video builds upon the concept of vector transformation rules from the 'Tensors for Beginners' series.
Vectors are expanded as linear combinations of basis vectors, with different components depending on the chosen basis.
Einstein summation notation is utilized to compactly represent basis vector expansions.
The contravariant nature of vector components is discussed, showing how they transform oppositely to basis vectors.
The geometrical interpretation of contravariance is provided, illustrating how basis vector size affects vector components.
Vector fields along curves are analyzed, showing their expansion in both Cartesian and polar bases.
The forward and backward transforms between Cartesian and polar basis vectors are introduced.
The transformation formula for the components of tangent vectors is derived using backward transformation.
The multivariable chain rule is highlighted as the foundation for deriving transformation formulas.
An example of a circular curve is used to concretely demonstrate the transformation of vector components.
The backward matrix B, or inverse Jacobian, is shown to correctly transform Cartesian components to polar components.
The forward matrix F, or Jacobian, is confirmed to convert polar components to Cartesian components accurately.
The video emphasizes that understanding the multivariable chain rule eliminates the need to memorize transformation formulas.
The position vector R is removed from formulas, leading to a focus on partial derivative operators as basis vectors.
Derivative operators are redefined as vectors, obeying transformation rules similar to ordinary vectors.
The rationale for eliminating the position vector R is explained in the context of future discussions on curved surfaces and manifolds.
Transcripts
Browse More Related Video

Tensor Calculus 4: Derivatives are Vectors
Tensors for Beginners 6: Covector Transformation Rules
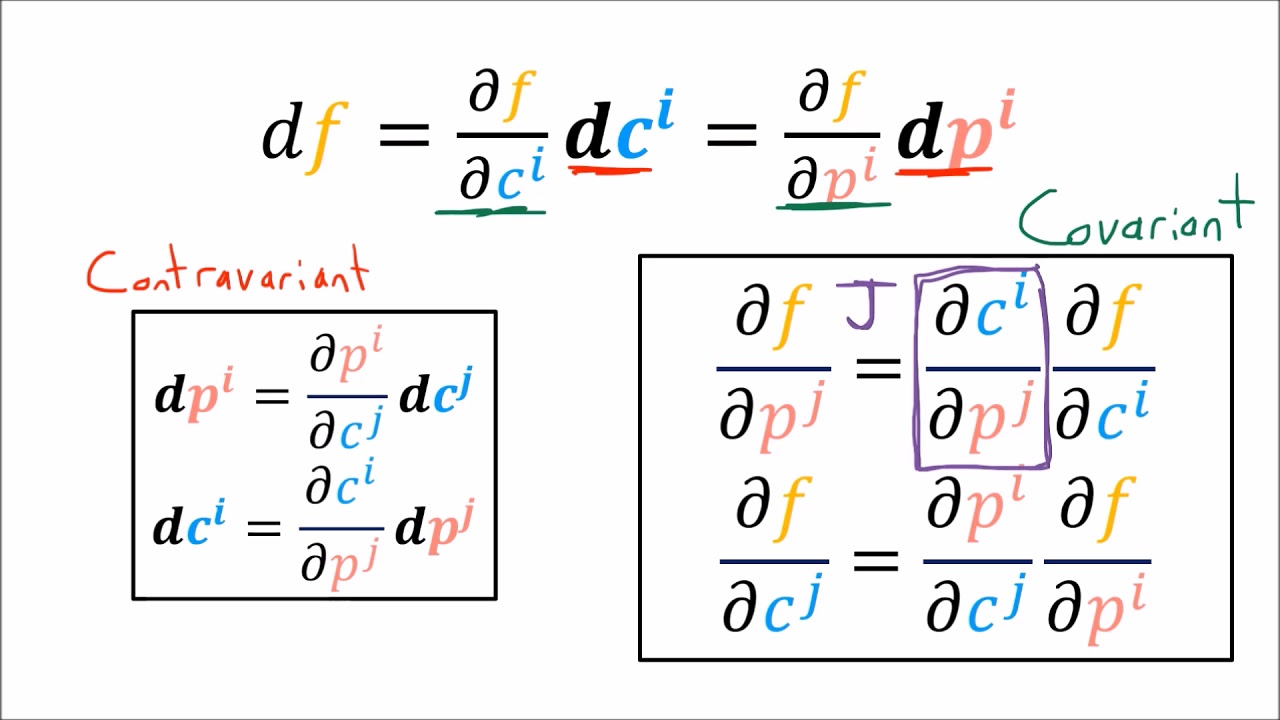
Tensor Calculus 8: Covector Field Transformation Rules (Covariance)

Tensors for Beginners 8: Linear Map Transformation Rules

Contravariant and Covariant Vectors | 2/2

Tensor Calculus 7: Covector Field Components
5.0 / 5 (0 votes)
Thanks for rating: